Published online by Cambridge University Press: 25 April 2022
This paper focuses on a 2D magnetohydrodynamic system with only horizontal dissipation in the domain $\Omega = \mathbb {T}\times \mathbb {R}$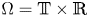 with $\mathbb {T}=[0,\,1]$
with $\mathbb {T}=[0,\,1]$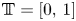 being a periodic box. The goal here is to understand the stability problem on perturbations near the background magnetic field $(1,\,0)$
being a periodic box. The goal here is to understand the stability problem on perturbations near the background magnetic field $(1,\,0)$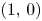 . Due to the lack of vertical dissipation, this stability problem is difficult. This paper solves the desired stability problem by simultaneously exploiting two smoothing and stabilizing mechanisms: the enhanced dissipation due to the coupling between the velocity and the magnetic fields, and the strong Poincaré type inequalities for the oscillation part of the solution, namely the difference between the solution and its horizontal average. In addition, the oscillation part of the solution is shown to converge exponentially to zero in $H^{1}$
. Due to the lack of vertical dissipation, this stability problem is difficult. This paper solves the desired stability problem by simultaneously exploiting two smoothing and stabilizing mechanisms: the enhanced dissipation due to the coupling between the velocity and the magnetic fields, and the strong Poincaré type inequalities for the oscillation part of the solution, namely the difference between the solution and its horizontal average. In addition, the oscillation part of the solution is shown to converge exponentially to zero in $H^{1}$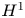 as $t\to \infty$
as $t\to \infty$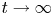 . As a consequence, the solution converges to its horizontal average asymptotically.
. As a consequence, the solution converges to its horizontal average asymptotically.