Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Colombo, Fabrizio
and
Sabadini, Irene
2012.
On some notions of spectra for quaternionic operators and for n-tuples of operators.
Comptes Rendus. Mathématique,
Vol. 350,
Issue. 7-8,
p.
399.
Alpay, Daniel
Colombo, Fabrizio
and
Sabadini, Irene
2013.
Pontryagin-de Branges-Rovnyak spaces of slice hyperholomorphic functions.
Journal d'Analyse Mathématique,
Vol. 121,
Issue. 1,
p.
87.
Vajiac, Mihaela B.
2013.
Advances in Hypercomplex Analysis.
Vol. 1,
Issue. ,
p.
125.
Colombo, Fabrizio
and
Sabadini, Irene M.
2014.
Operator Theory.
p.
1.
Colombo, Fabrizio
and
Sabadini, Irene
2014.
TheF-functional calculus for unbounded operators.
Journal of Geometry and Physics,
Vol. 86,
Issue. ,
p.
392.
Alpay, Daniel
Colombo, F.
and
Sabadini, I.
2014.
On some notions of convergence forn‐tuples of operators.
Mathematical Methods in the Applied Sciences,
Vol. 37,
Issue. 16,
p.
2363.
Alpay, Daniel
Colombo, Fabrizio
and
Sabadini, Irene
2014.
Krein–Langer Factorization and Related Topics in the Slice Hyperholomorphic Setting.
The Journal of Geometric Analysis,
Vol. 24,
Issue. 2,
p.
843.
Colombo, Fabrizio
and
Sabadini, Irene
2015.
Operator Theory.
p.
1787.
Cnudde, Lander
De Bie, Hendrik
and
Ren, Guangbin
2015.
Algebraic Approach to Slice Monogenic Functions.
Complex Analysis and Operator Theory,
Vol. 9,
Issue. 5,
p.
1065.
Alpay, Daniel
Colombo, Fabrizio
Gantner, Jonathan
and
Sabadini, Irene
2015.
A New Resolvent Equation for the $$S$$ S -Functional Calculus.
The Journal of Geometric Analysis,
Vol. 25,
Issue. 3,
p.
1939.
Colombo, Fabrizio
and
Gantner, Jonathan
2016.
On power series expansions of the S-resolvent operator and the Taylor formula.
Journal of Geometry and Physics,
Vol. 110,
Issue. ,
p.
154.
Colombo, Fabrizio
and
Gantner, Jonathan
2018.
An Application of the S-Functional Calculus to Fractional Diffusion Processes.
Milan Journal of Mathematics,
Vol. 86,
Issue. 2,
p.
225.
Colombo, Fabrizio
and
Gantner, Jonathan
2018.
Fractional powers of vector operators and fractional Fourier’s law in a Hilbert space.
Journal of Physics A: Mathematical and Theoretical,
Vol. 51,
Issue. 30,
p.
305201.
Colombo, Fabrizio
Mongodi, Samuele
Peloso, Marco
and
Pinton, Stefano
2019.
Fractional powers of the noncommutative Fourier's law by the S‐spectrum approach.
Mathematical Methods in the Applied Sciences,
Vol. 42,
Issue. 5,
p.
1662.
Colombo, Fabrizio
Peloso, Marco M.
and
Pinton, Stefano
2019.
The structure of the fractional powers of the noncommutative Fourier law.
Mathematical Methods in the Applied Sciences,
Vol. 42,
Issue. 18,
p.
6259.
Colombo, Fabrizio
Deniz González, Denis
and
Pinton, Stefano
2020.
Fractional powers of vector operators with first order boundary conditions.
Journal of Geometry and Physics,
Vol. 151,
Issue. ,
p.
103618.
Colombo, Fabrizio
Sabadini, Irene
and
Struppa, Daniele C.
2020.
Michele Sce's Works in Hypercomplex Analysis.
p.
69.
Colombo, Fabrizio
Gantner, Jonathan
and
Pinton, Stefano
2021.
An Introduction to Hyperholomorphic Spectral Theories and Fractional Powers of Vector Operators.
Advances in Applied Clifford Algebras,
Vol. 31,
Issue. 3,
de Martino, Antonino
and
Pinton, Stefano
2023.
A polyanalytic functional calculus of order 2 on the 𝑆-spectrum.
Proceedings of the American Mathematical Society,
Colombo, Fabrizio
De Martino, Antonino
and
Sabadini, Irene
2023.
The $$\mathcal {F}$$-Resolvent Equation and Riesz Projectors for the $$\mathcal {F}$$-Functional Calculus.
Complex Analysis and Operator Theory,
Vol. 17,
Issue. 2,
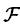 -spectrum and the
-spectrum and the 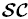 -functional calculus
-functional calculus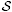 -functional calculus) for n-tuples of both bounded and unbounded not-necessarily commuting operators. The
-functional calculus) for n-tuples of both bounded and unbounded not-necessarily commuting operators. The 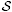 -functional calculus is based on the notion of
-functional calculus is based on the notion of 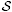 -spectrum, which naturally arises from the definition of the
-spectrum, which naturally arises from the definition of the 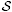 -resolvent operator for n-tuples of operators. The
-resolvent operator for n-tuples of operators. The 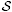 -resolvent operator plays the same role as the usual resolvent operator for the Riesz–Dunford functional calculus, which is associated to a complex operator acting on a Banach space. When one considers commuting operators (bounded or unbounded) there is the possibility of simplifying the computation of the
-resolvent operator plays the same role as the usual resolvent operator for the Riesz–Dunford functional calculus, which is associated to a complex operator acting on a Banach space. When one considers commuting operators (bounded or unbounded) there is the possibility of simplifying the computation of the 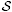 -spectrum. In fact, in this case we can use the F-spectrum, which is easier to compute than the
-spectrum. In fact, in this case we can use the F-spectrum, which is easier to compute than the 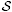 -spectrum. In the case of commuting operators, our functional calculus is based on the
-spectrum. In the case of commuting operators, our functional calculus is based on the 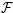 -spectrum and will be called
-spectrum and will be called 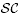 -functional calculus. We point out that for a correct definition of the
-functional calculus. We point out that for a correct definition of the 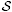 -resolvent operator and of the
-resolvent operator and of the 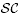 -resolvent operator in the unbounded case we have to face different extension problems. Another reason for a more detailed study of the
-resolvent operator in the unbounded case we have to face different extension problems. Another reason for a more detailed study of the 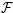 -spectrum is that it is related to the
-spectrum is that it is related to the 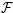 -functional calculus which is based on the integral version of the Fueter mapping theorem. This functional calculus is associated to monogenic functions constructed by starting from slice monogenic functions.
-functional calculus which is based on the integral version of the Fueter mapping theorem. This functional calculus is associated to monogenic functions constructed by starting from slice monogenic functions.

