Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T08:46:38.215Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral theory for a class of pseudodifferential operators

Published online by Cambridge University Press:  14 February 2012

E. A. Catchpole
E. A. Catchpole
Affiliation:
Royal Military College, Duntroon, Australia
Get access Rights & Permissions [Opens in a new window]

Synopsis

We investigate the spectral theory for a class of pseudodifferential operators which includes all constant coefficient differential operators, and also operators such as 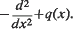The operators considered are of the form Su(x) = Au(x)+q(x)u(x), where A is an operator which corresponds in the Fourier transform plane to a multiplication operator, and q(x) is a potential term. We prove an eigenfunction expansion theorem for S and derive some results concerning the spectrum of S.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 76 , Issue 3 , 1977 , pp. 197 - 214
Copyright
Copyright © Royal Society of Edinburgh 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Akhiezer, N. I. and Glazman, I. M.. Theory of linear operators in Hilbert space, I and II. (New York: Ungar, 1961).Google Scholar
2Benjamin, T. B.. Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 29 (1967), 559–592.CrossRefGoogle Scholar
3Benjamin, T. B.. The stability of solitary waves. Proc. Roy. Soc. London Ser. A 328 (1972), 153–183.Google Scholar
4Benjamin, T. B., Bona, J. L. and Mahony, J. J.. Model equations for long waves in nonlinear dispersive systems. Philos. Trans. Roy. Soc. London Ser. A 272 (1972), 47–78.Google Scholar
5Berezanskii, Ju.M.. Expansions in eigenfunctions of selfadjoint operators (Providence: Amer. Math. Soc., 1968).CrossRefGoogle Scholar
6Butzer, P. L. and Nessel, R. J.. Fourier analysis and approximation, I (Basel: Birkhauser, 1971).CrossRefGoogle Scholar
7N. Dunford and Schwartz, J. T.. Linear operators, II (New York: Interscience, 1963).Google Scholar
8Friedrichs, K. O.. Pseudo-differential operators: an introduction: lectures given in 1967-68 at the Courant Institute (New York: Courant Inst. Math. Sci., 1968).Google Scholar
9Gel'fand, I. M. and Vilenkin, N. Ya.. Generalized functions, 4 (New York: Academic Press, 1964).Google Scholar
10Jörgens, K.. Spectral theory of second-order ordinary differential operators (Aarhus: University, 1964).Google Scholar
11Kato, T.. Perturbation theory for linear operators (Berlin: Springer, 1966).Google Scholar
12Peetre, J.. Rectification a l'article ‘Une caracterization abstraite des operateurs differentiels’. Math. Scand. 8 (1960), 116–120.CrossRefGoogle Scholar
13Pritchard, W. G.. Solitary waves in rotating fluids. J. Fluid Mech., 42 (1970), 61–83.CrossRefGoogle Scholar
14Schechter, M.. Spectra of partial differential operators (Amsterdam: North-Holland, 1971).Google Scholar
15Stone, M. H.. Linear transformations in Hilbert space (Providence: Amer. Math. Soc., 1932).Google Scholar
16Taylor, M.. Pseudo differential operators (New York: Springer, 1974).CrossRefGoogle Scholar