Published online by Cambridge University Press: 28 November 2024
We consider the existence and stability of constrained solitary wave solutions to the generalized Ostrovsky equation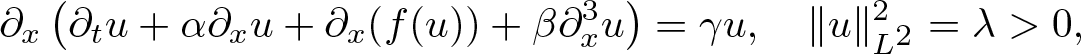 \begin{align*}\partial_x\left(\partial_t u+ \alpha\partial_x u+\partial_x(f(u))+\beta \partial_x^3u\right)=\gamma u,\quad \|u\|_{L^2}^2=\lambda \gt 0,\end{align*}
\begin{align*}\partial_x\left(\partial_t u+ \alpha\partial_x u+\partial_x(f(u))+\beta \partial_x^3u\right)=\gamma u,\quad \|u\|_{L^2}^2=\lambda \gt 0,\end{align*}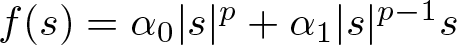 $f(s)=\alpha_0|s|^p+\alpha_1|s|^{p-1}s$, with p > 1. If
$f(s)=\alpha_0|s|^p+\alpha_1|s|^{p-1}s$, with p > 1. If 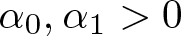 $\alpha_0,\alpha_1 \gt 0$,
$\alpha_0,\alpha_1 \gt 0$, 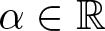 $\alpha\in\mathbb{R}$, and γ < 0 satisfying
$\alpha\in\mathbb{R}$, and γ < 0 satisfying 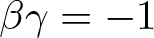 $\beta\gamma=-1$, we show that for
$\beta\gamma=-1$, we show that for 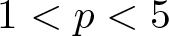 $1 \lt p \lt 5$, there exists a constrained ground state traveling wave solution with travelling velocity
$1 \lt p \lt 5$, there exists a constrained ground state traveling wave solution with travelling velocity 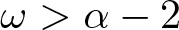 $\omega \gt \alpha-2$. Furthermore, we obtain the exponential decay estimates and the weak non-degeneracy of the solution. Finally, we show that the solution is spectrally stable. This is a continuation of recent work [1] on existence and stability for a water wave model with non-homogeneous nonlinearities.
$\omega \gt \alpha-2$. Furthermore, we obtain the exponential decay estimates and the weak non-degeneracy of the solution. Finally, we show that the solution is spectrally stable. This is a continuation of recent work [1] on existence and stability for a water wave model with non-homogeneous nonlinearities.