Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T08:41:06.694Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral analysis of the Epstein operator

Published online by Cambridge University Press:  14 November 2011

J. C. Guillot  and
C. H. Wilcox
J. C. Guillot
Affiliation:
Département de Mathématiques, Université de Paris Nord, 93430 Villetaneuse, France
C. H. Wilcox
Affiliation:
Department of Mathematics, University of Utah, Salt Lake City, Utah 84112, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The Epstein operator is defined by

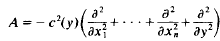
where x = (x1, …, xn) ∈ Rn, y ∈ R,

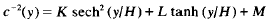
and H, K, L, M are real constants such that c2(y) > 0. The operator arises in the study of acoustic wave propagation in plane-stratified fluids with sound speed c(y) at depth y. In this paper it is shown that A defines a selfadjoint operator in the Hilbert space ℋ = L2(Rn + 1c−2(y) dx dy) where dx = dx1 … dxn. The spectral family of A is constructed, the spectrum is shown to be continuous and an eigenfunction expansion for A is given in terms of families of improper eigenfunctions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 80 , Issue 1-2 , 1978 , pp. 85 - 98
Copyright
Copyright © Royal Society of Edinburgh 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Deavenport, R. L.A normal mode theory of an underwater acoustic duct by means of Green's function. Radio Sci. 1 (1966), 709–724.CrossRefGoogle Scholar
2Dunford, N. and Schwartz, J. T.Linear Operators, II: Spectral Theory (New York: Interscience, 1963).Google Scholar
3Epstein, P. S.Reflection of waves in an inhomogeneous absorbing medium. Proc. Nat. Acad. Sci. U.S.A. 16 (1930), 627–637.CrossRefGoogle Scholar
4Guillot, J. C. and Wilcox, C. H.Théorie spectral de l'opérateur d'Epstein. C.R. Acad. Sci. Paris Ser. A-B 281 (1975), 399–402.Google Scholar
5Guillot, J. C. and Wilcox, C. H.Spectral analysis of the Epstein operator. Utah Univ. O.N.R. Tech. Summary Report 27 (1975).Google Scholar
6Magnus, W., Oberhettinger, F. and Soni, R. P.Formulas and Theorems for the Special Functions of Mathematical Physics (New York: Springer, 1966).Google Scholar
7Pedersen, M. A. and White, D. W.Ray theory of the general Epstein profile. J. Acoust. Soc. Amer. 44 (1968), 765–786.CrossRefGoogle Scholar
8Wilcox, C. H.Transient acoustic wave propagation in a symmetric Epstein duct. Utah Univ. O.N.R. Tech. Summary Report 25 (1974).Google Scholar
9Wilcox, C. H.Spectral analysis of the Pekeris operator. Arch. Rational Mech. Anal. 60 (1976), 259–300.CrossRefGoogle Scholar