Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-21T14:56:03.406Z Has data issue: false hasContentIssue false
  • English
  • Français

The spectra of well-posed operators

Published online by Cambridge University Press:  14 November 2011

Sobhy El-sayed Ibrahim
Sobhy El-sayed Ibrahim
Affiliation:
Benha University, Faculty of Science, Department of Mathematics, Benha B 13518, Egypt
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, the general ordinary quasidifferential expression M of nth order, with complex coefficients, and its formal adjoint M− are considered. It is shown in the case of two singular endpomts and when all solutions of the equation and the adjoint equation are in 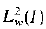(the limit-circle case) that all well-posed extensions of the minimal operator T0(M) have resolvents which are Hilbert Schmidt integral operators and consequently have a wholly discrete spectrum. This implies that all the regularly solvable operators have all of the standard essential spectra to be empty. These results extend those for the formally symmetric expression M studied in [1] and [14], and also extend those proved in [8] for one singular endpoint.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 125 , Issue 6 , 1995 , pp. 1331 - 1348
Copyright
Copyright © Royal Society of Edinburgh 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Akhiezer, N. I. and Glazman, I. M.. Theory of Linear Operators in Hitbert Spaec (New York: Fredcrich Uogar. Vol. I 1961. Vol. II 1963).Google Scholar
2Edmunds, D. E. and Evans, W. D.. Spectral Theory and Differential Operators (Oxford University Press. 1987).Google Scholar
3Evans, W. D.. Regularly solvable extensions of non-self-adjoint ordinary diftercntial operators. Proc. Roy. Soc. Edinburgh Sect. A 97 (1984), 79–95.CrossRefGoogle Scholar
4Evans, W. D. and Ibrahim, Sobhy E.. Boundary conditions for general ordinary differential operators and their adjoints. Proc. Roy. Soc. Edinburgh Sect. A 114 (1990), 99–117.CrossRefGoogle Scholar
5Everitt, W. N. and Race, D.. Some remarks on linear ordinary quasi-differential equations. Proc. London Math. Soc. (3)54(1987), 300–20.CrossRefGoogle Scholar
6Everitt, W. N. and Zettl, A.. Generalized symmetric ordinary differential expressions I: the general theory. Nieuw Arch. Wish. (3) 27 (1979), 363 97.Google Scholar
7Everitt, W. N. and Zettl, A.. Sturm-Liouville differential operators in direct sum spaces. Rocky Mountain J. Math. 16 (1986). 497–516.CrossRefGoogle Scholar
8Ibrahim, Sobhy E.. Problems associated with differential operators (Ph.D. thesis. Faculty of Science, Benha University, Egypt, 1989).Google Scholar
9Ibrahim, Sobhy E.. The point spectra and regularity fields of non-self adjoint quasi-differential operators. Rocky Mountain J. Math. 24, No. 4 (Fall 1994).Google Scholar
10Ibrahim, Sobhy E.. Singular non-self-adjoint differential operators. Proc. Roy. Soc. Edinburgh Sect. A 124(1994), 825 41.CrossRefGoogle Scholar
11Kimura, T. and Takahasi, M.. Sur les operateurs différentiels ordinaires linéaires formellement autoadjoints I. Funkcial. Ekvac. 7 (1965), 35–90.Google Scholar
12Krall, A. N. and Zettl, A.. Singular self-adjoint Strum-Liouville problems. J. Differential Integral Equations 1 (1988). 423–32.Google Scholar
13Lucker, J.. functional Analysis for Two-point Differential Operators, Pilman Research Notes in Mathematics 144 (Harlow, Essex: Longman Scientific and Technical, 1986).Google Scholar
14Naimark, M. A.. Linear Differential Operators, Part II (New York: Frederich Ullgar, 1968).Google Scholar
15Visik, M.I.. On general boundary problems for elliptic differential equations. Trans. Amer. Math. Soc. (2) 24(1963), 107–72.Google Scholar
16Walker, W. P.. Weighted singular differential operators in the limit-circle case. J. London Math. Soc. (2) 4(1972), 741–4.CrossRefGoogle Scholar
17Zettl, A.. Formally self-adjoint quasi-differential operators. Rocky Mountain J. Math. 5 (1975), 453 74.CrossRefGoogle Scholar
18Zhikhar, N. A.. The theory of extension of J-symmetric operators. Ukrafn. Mat. Zh. 11 (1959). 352–65.Google Scholar