Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-15T09:49:27.591Z Has data issue: false hasContentIssue false
  • English
  • Français

Spaces of functions and sections with paracompact domain

Part of: Homotopy theory Spectral sequences

Published online by Cambridge University Press:  21 November 2023

Jaka Smrekar Open the ORCID record for Jaka Smrekar [Opens in a new window]
Jaka Smrekar*
Affiliation:
Fakulteta za matematiko in fiziko, Jadranska ulica 19, SI-1111 Ljubljana, Slovenia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study spaces of continuous functions and sections with domain a paracompact Hausdorff k-space $X$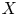 and range a nilpotent CW complex $Y$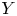, with emphasis on localization at a set of primes. For $\mathop {\rm map}\nolimits _\phi (X,\,Y)$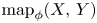, the space of maps with prescribed restriction $\phi$ 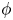on a suitable subspace $A\subset X$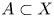, we construct a natural spectral sequence of groups that converges to $\pi _*(\mathop {\rm map}\nolimits _\phi (X,\,Y))$ 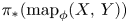and allows for detection of localization on the level of $E^2$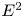. Our applications extend and unify the previously known results.

Keywords

Function spaceFederer spectral sequencelocalization

MSC classification

Primary: 55T99: None of the above, but in this section 55P60: Localization and completion 55P15: Classification of homotopy type
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 23
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barratt, M. G.. Track groups. II. Proc. London Math. Soc. (3) 5 (1955), 285–329.CrossRefGoogle Scholar
Baues, H. J.. Algebraic Homotopy (Cambridge Univ. Press, Cambridge, 1989).CrossRefGoogle Scholar
Bredon, G. E.. Sheaf theory. Graduate Texts in Mathematics Vol. 170 (Springer-Verlag, Berlin/New York, 1997).CrossRefGoogle Scholar
Brown, R. and Heath, P. R.. Coglueing homotopy equivalences. Math. Z. 113 (1970), 313–325.CrossRefGoogle Scholar
Bousfield, A. K. and Kan, D.. Homotopy limits, completions and localizations. Lecture Notes in Mathematics, Vol. 304 (Springer-Verlag, Berlin/New York, 1972).CrossRefGoogle Scholar
Dowker, C. H.. Čech cohomology theory and the axioms. Ann. Math. (2) 51 (1950), 278–292.CrossRefGoogle Scholar
Farjoun, E. D. and Schochet, C. L.. Spaces of sections of Banach algebra bundles. J. K-Theory 10 (2012), 279–298.CrossRefGoogle Scholar
Dyer, M.. Federer-Čech couples. Canadian J. Math. 21 (1969), 842–864.CrossRefGoogle Scholar
Dugundji, J.. Topology (Allyn & Bacon Inc, Boston, MA, 1966).Google Scholar
Federer, H.. A study of function spaces by spectral sequences. Trans. Amer. Math. Soc. 82 (1956), 340–361.CrossRefGoogle Scholar
Goto, T.. Homotopical cohomology groups of paracompact spaces. Sci. Rep. Tokyo Kyoiku Daigaku Sect. A 9 (1967), 163–169.Google Scholar
Hilton, P., Mislin, G. and Roitberg, J.. Localization of nilpotent groups and spaces. North-Holland Mathematics Studies, Vol. 15 (North-Holland, Amsterdam, 1975).Google Scholar
Hilton, P., Mislin, G., Roitberg, J. and Steiner, R.. On free maps and free homotopies into nilpotent spaces. Algebraic topology (Proc. Conf., Vancouver, 1977), Lecture Notes in Math, Vol. 673 (Springer, Berlin, 1978).CrossRefGoogle Scholar
Huber, P. J.. Homotopical cohomology and Čech cohomology. Math. Ann. 144 (1961), 73–76.CrossRefGoogle Scholar
Kahn, D. S.. An example in Čech cohomology. Proc. Amer. Math. Soc. 16 (1965), 584.Google Scholar
Klein, J. R., Schochet, C. L. and Smith, S. B.. Continuous trace C$^*$-algebras, gauge groups and rationalization. J. Topol. Anal. 1 (2009), 261–288.CrossRefGoogle Scholar
Mardešić, S. and Segal, J.. Shape theory. The inverse system approach. North-Holland Mathematical Library, Vol. 26 (North-Holland Publishing Co, Amsterdam/New York, 1982).Google Scholar
Maunder, C. R. F.. Algebraic topology (Dover Publications Inc, Mineola, New York, 1996).Google Scholar
May, J. P. and Ponto, K.. More concise algebraic topology. Localization, completion, and model categories. Chicago Lectures in Mathematics (University of Chicago Press, Chicago, IL, 2012).CrossRefGoogle Scholar
May, J. P. and Sigurdsson, J.. Parametrized homotopy theory. Mathematical Surveys and Monographs, Vol. 132 (American Mathematical Society, Providence, RI, 2006).CrossRefGoogle Scholar
Michael, E.. Continuous selections. I. Ann. of Math. (2) 63 (1956), 361–382.CrossRefGoogle Scholar
Milnor, J.. On spaces having the homotopy type of a CW-complex. Trans. Amer. Math. Soc. 90 (1959), 272–280.Google Scholar
Miyata, T.. Fibrations in the category of absolute neighborhood retracts. Bull. Pol. Acad. Sci. Math. 55 (2007), 145–154.CrossRefGoogle Scholar
Møller, J. M.. Nilpotent spaces of sections. Trans. Amer. Math. Soc. 303 (1987), 733–741.CrossRefGoogle Scholar
Sakai, K.. Geometric aspects of general topology. Springer Monographs in Mathematics (Springer, Tokyo, 2013).CrossRefGoogle Scholar
Schochet, C. L. and Smith, S. B.. Localization of grouplike function and section spaces with compact domain. Homotopy theory of function spaces and related topics, 189–202, Contemp. Math., Vol. 519 (Amer. Math. Soc, Providence, RI, 2010).CrossRefGoogle Scholar
Smith, S. B.. A based Federer spectral sequence and the rational homotopy of function spaces. Manuscripta Math. 93 (1997), 59–66.CrossRefGoogle Scholar
Smrekar, J.. CW type of inverse limits and function spaces. e-print arXiv:0708.2838 [math.AT].Google Scholar
Smrekar, J.. Homotopy type of mapping spaces and existence of geometric exponents. Forum Math. 22 (2010), 433–456.CrossRefGoogle Scholar
Smrekar, J.. Homotopy type of space of maps into a $K(G,\,n)$. Homology Homotopy Appl. 15 (2013), 137–149.CrossRefGoogle Scholar
Smrekar, J.. CW towers and mapping spaces. Topol. Appl. 194 (2015), 93–117.CrossRefGoogle Scholar
Spanier, E. H.. Borsuk's cohomotopy groups. Ann. Math. (2) 50 (1949), 203–245.CrossRefGoogle Scholar
Stasheff, J.. A classification theorem for fibre spaces. Topology 2 (1963), 239–246.CrossRefGoogle Scholar
Stramaccia, L.. P-embeddings, AR and ANR spaces. Homology Homotopy Appl. 5 (2003), 213–218.CrossRefGoogle Scholar
Strøm, A.. Note on cofibrations II. Math. Scand. 22 (1968), 130–142.CrossRefGoogle Scholar