Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T19:49:51.684Z Has data issue: false hasContentIssue false
  • English
  • Français

Some generic properties of Schrödinger operators with radial potentials

Part of: Elliptic equations and systems Spectral theory and eigenvalue problems General theory of linear operators

Published online by Cambridge University Press:  15 January 2019

Peter Poláčik  and
Darío A. Valdebenito
Peter Poláčik
Affiliation:
School of Mathematics, University of Minnesota, Minneapolis, MN 55455, USA ([email protected])
Darío A. Valdebenito
Affiliation:
Department of Mathematics and Statistics, McMaster University Hamilton, ON L8S 4K1, Canada ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a class of Schrödinger operators on 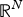${\open R}^N$ with radial potentials. Viewing them as self-adjoint operators on the space of radially symmetric functions in 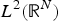$L^2({\open R}^N)$, we show that the following properties are generic with respect to the potential:

  1. (P1) the eigenvalues below the essential spectrum are nonresonant (i.e., rationally independent) and so are the square roots of the moduli of these eigenvalues;

  2. (P2) the eigenfunctions corresponding to the eigenvalues below the essential spectrum are algebraically independent on any nonempty open set.

The genericity means that in suitable topologies the potentials having the above properties form a residual set. As we explain, (P1), (P2) are prerequisites for some applications of KAM-type results to nonlinear elliptic equations. Similar properties also play a role in optimal control and other problems in linear and nonlinear partial differential equations.

Keywords

Schrödinger operatorsradial potentialsrational independence of eigenvaluesalgebraic independence of eigenfunctionsgeneric properties

MSC classification

Primary: 35J10: Schrödinger operator
Secondary: 35P99: None of the above, but in this section 47A75: Eigenvalue problems 47A55: Perturbation theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 6 , December 2019 , pp. 1435 - 1451
Copyright
Copyright © Royal Society of Edinburgh 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Agmon, S.. Lectures on exponential decay of solutions of second-order elliptic equations: bounds on eigenfunctions of N-body Schrödinger operators. Mathematical Notes, vol. 29, (Princeton, NJ: Princeton University Press, University of Tokyo Press, Tokyo, 1982).Google Scholar
2Bambusi, D.. An introduction to Birkhoff normal form (Italy: Università di Milano, 2014).Google Scholar
3Bambusi, D. and Grébert, B.. Birkhoff normal form for partial differential equations with tame modulus. Duke Math. J. 135 (2006), 507–567.Google Scholar
4Berestycki, H. and Lions, P.-L.. Nonlinear scalar field equations. I. Existence of a ground state. Arch. Rational Mech. Anal. 82 (1983), 313–345.Google Scholar
5Chambrion, T., Mason, P., Sigalotti, M. and Boscain, U.. Controllability of the discrete-spectrum Schrödinger equation driven by an external field. Ann. Inst. H. Poincaré Anal. Non Linéaire 26 (2009), 329–349.Google Scholar
6Craig, W. and Wayne, C. E.. Newton's method and periodic solutions of nonlinear wave equations. Comm. Pure Appl. Math. 46 (1993), 1409–1498.Google Scholar
7Dancer, E. N. and Poláčik, P.. Realization of vector fields and dynamics of spatially homogeneous parabolic equations. Mem. Amer. Math. Soc. 140 (1999), viii+82.Google Scholar
8Davies, E. B.. Spectral theory and differential operators. Cambridge Studies in Advanced Mathematics, vol. 42 (Cambridge: Cambridge University Press, 1995).Google Scholar
9Fiedler, B. and Poláčik, P.. Complicated dynamics of scalar reaction diffusion equations with a nonlocal term. Proc. Roy. Soc. Edinburgh Sect. A 115 (1990), 167–192.Google Scholar
10Gårding, L.. On the essential spectrum of Schrödinger operators. J. Funct. Anal. 52 (1983), 1–10.Google Scholar
11Hébrard, P. and Henrot, A.. A spillover phenomenon in the optimal location of actuators. SIAM J. Control Optim. 44 (2005), 349–366.Google Scholar
12Henry, D.. Perturbation of the boundary for boundary value problems of partial differential operators (Cambridge: Cambridge University Press, 2005).Google Scholar
13Hislop, P. D. and Sigal, I. M.. Introduction to spectral theory. Applied Mathematical Sciences, vol. 113 (New York: Springer-Verlag, 1996), With applications to Schrödinger operators.Google Scholar
14Kato, T.. Perturbation theory for linear operators (Berlin: Springer-Verlag, 1966).Google Scholar
15Kuksin, S.B.. Hamiltonian PDEs.In Handbook of dynamical systems, vol. 1B, pp. 1087–1133 (Amsterdam: Elsevier B. V., 2006, With an appendix by Dario Bambusi.Google Scholar
16Mason, P. and Sigalotti, M.. Generic controllability properties for the bilinear Schrödinger equation. Comm. Partial Diff. Equ. 35 (2010), 685–706.Google Scholar
17Metafune, G. and Schnaubelt, R.. The domain of the Schrödinger operator $-\Delta +x^2y^2$. Note Mat. 25 (2005/06), 97–103.Google Scholar
18Metafune, G., Prüss, J., Schnaubelt, R. and Rhandi, A.. L p-regularity for elliptic operators with unbounded coefficients. Adv. Diff. Equ. 10 (2005), 1131–1164.Google Scholar
19Persson, A.. Bounds for the discrete part of the spectrum of a semi-bounded Schrödinger operator. Math. Scand. 8 (1960), 143–153.Google Scholar
20Poláčik, P.. High-dimensional ω-limit sets and chaos in scalar parabolic equations. J. Diff. Equ. 119 (1995), 24–53.Google Scholar
21 Poláčik, P.. Parabolic equations: asymptotic behavior and dynamics on invariant manifolds. In Handbook on dynamical systems, vol. 2 (ed.Fiedler, B.), pp. 835–883 (Amsterdam: Elsevier, 2002).Google Scholar
22Poláčik, P. and Valdebenito, D. A.. Existence of quasiperiodic solutions of elliptic equations on ${\open R}^{N+1}$ via center manifold and KAM theorems. J. Diff. Equ. 262 (2017), 6109–6164.Google Scholar
23Privat, Y. and Sigalotti, M.. The squares of the Laplacian-Dirichlet eigenfunctions are generically linearly independent. ESAIM Control Optim. Calc. Var. 16 (2010), 794–805. Erratum: 16 (2010), 806–807.Google Scholar
24Prizzi, M. and Rybakowski, K. P.. Complicated dynamics of parabolic equations with simple gradient dependence. Trans. Amer. Math. Soc. 350 (1998a), 3119–3130.Google Scholar
25Prizzi, M. and Rybakowski, K. P.. Inverse problems and chaotic dynamics of parabolic equations on arbitrary spatial domains. J. Diff. Equ. 142 (1998b), 17–53.Google Scholar
26Reed, M. and Simon, B.. Methods of mathematical physics, vol. IV New York: Academic Press, 1978).Google Scholar
27Scheurle, J.. Bifurcation of quasiperiodic solutions from equilibrium points of reversible dynamical systems. Arch. Rational Mech. Anal. 97 (1987), 103–139.Google Scholar
28Teytel, M.. How rare are multiple eigenvalues?. Comm. Pure Appl. Math. 52 (1999), 917–934.Google Scholar
29Valls, C.. Existence of quasi-periodic solutions for elliptic equations on a cylindrical domain. Comment. Math. Helv. 81 (2006), 783–800.Google Scholar
30Wayne, C. E.. Periodic and quasi-periodic solutions of nonlinear wave equations via KAM theory. Comm. Math. Phys. 127 (1990), 479–528.Google Scholar
31Zuazua, E.. Switching control. J. Eur. Math. Soc. (JEMS) 13 (2011), 85–117.Google Scholar