No CrossRef data available.
Published online by Cambridge University Press: 27 December 2018
Let n ⩾ 3, 0 ⩽ m < n − 2/n, ρ1 > 0, 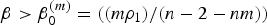 $\beta>\beta_{0}^{(m)}=(({m\rho_{1}})/({n-2-nm}))$, αm = ((2β + ρ1)/(1 − m)) and α = 2β+ρ1. For any λ > 0, we prove the uniqueness of radially symmetric solution υ(m) of Δ(υm/m) + αmυ + βx · ∇υ = 0, υ > 0, in ℝn∖{0} which satisfies
$\beta>\beta_{0}^{(m)}=(({m\rho_{1}})/({n-2-nm}))$, αm = ((2β + ρ1)/(1 − m)) and α = 2β+ρ1. For any λ > 0, we prove the uniqueness of radially symmetric solution υ(m) of Δ(υm/m) + αmυ + βx · ∇υ = 0, υ > 0, in ℝn∖{0} which satisfies 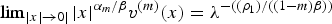 $\lim\nolimits_{|x|\to 0|}|x|^{\alpha _m/\beta }v^{(m)}(x) = \lambda ^{-((\rho _1)/((1-m)\beta ))}$ and obtain higher order estimates of υ(m) near the blow-up point x = 0. We prove that as m → 0+, υ(m) converges uniformly in C2(K) for any compact subset K of ℝn∖{0} to the solution υ of Δlog υ + α υ + β x·∇ υ = 0, υ > 0, in ℝn\{0}, which satisfies
$\lim\nolimits_{|x|\to 0|}|x|^{\alpha _m/\beta }v^{(m)}(x) = \lambda ^{-((\rho _1)/((1-m)\beta ))}$ and obtain higher order estimates of υ(m) near the blow-up point x = 0. We prove that as m → 0+, υ(m) converges uniformly in C2(K) for any compact subset K of ℝn∖{0} to the solution υ of Δlog υ + α υ + β x·∇ υ = 0, υ > 0, in ℝn\{0}, which satisfies 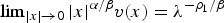 $\lim\nolimits_{ \vert x \vert \to 0} \vert x \vert ^{{\alpha}/{\beta}}v(x)=\lambda^{-{\rho_{1}}/{\beta}}$. We also prove that if the solution u(m) of ut = Δ (um/m), u > 0, in (ℝn∖{0}) × (0, T) which blows up near {0} × (0, T) at the rate
$\lim\nolimits_{ \vert x \vert \to 0} \vert x \vert ^{{\alpha}/{\beta}}v(x)=\lambda^{-{\rho_{1}}/{\beta}}$. We also prove that if the solution u(m) of ut = Δ (um/m), u > 0, in (ℝn∖{0}) × (0, T) which blows up near {0} × (0, T) at the rate 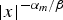 $ \vert x \vert ^{-{\alpha_{m}}/{\beta}}$ satisfies some mild growth condition on (ℝn∖{0}) × (0, T), then as m → 0+, u(m) converges uniformly in C2 + θ, 1 + θ/2(K) for some constant θ ∈ (0, 1) and any compact subset K of (ℝn∖{0}) × (0, T) to the solution of ut = Δlog u, u > 0, in (ℝn∖{0}) × (0, T). As a consequence of the proof, we obtain existence of a unique radially symmetric solution υ(0) of Δ log υ + α υ + β x·∇ υ = 0, υ > 0, in ℝn∖{0}, which satisfies
$ \vert x \vert ^{-{\alpha_{m}}/{\beta}}$ satisfies some mild growth condition on (ℝn∖{0}) × (0, T), then as m → 0+, u(m) converges uniformly in C2 + θ, 1 + θ/2(K) for some constant θ ∈ (0, 1) and any compact subset K of (ℝn∖{0}) × (0, T) to the solution of ut = Δlog u, u > 0, in (ℝn∖{0}) × (0, T). As a consequence of the proof, we obtain existence of a unique radially symmetric solution υ(0) of Δ log υ + α υ + β x·∇ υ = 0, υ > 0, in ℝn∖{0}, which satisfies 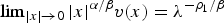 $\lim\nolimits_{ \vert x \vert \to 0} \vert x \vert ^{{\alpha}/{\beta}}v(x)=\lambda^{-{\rho_{1}}/{\beta}}$.
$\lim\nolimits_{ \vert x \vert \to 0} \vert x \vert ^{{\alpha}/{\beta}}v(x)=\lambda^{-{\rho_{1}}/{\beta}}$.