Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T11:40:38.912Z Has data issue: false hasContentIssue false
  • English
  • Français

Shadowing for infinite dimensional dynamics and exponential trichotomies

Part of: Smooth dynamical systems: general theory Stability theory

Published online by Cambridge University Press:  24 June 2020

Lucas Backes  and
Davor Dragičević
Lucas Backes
Affiliation:
Departamento de Matemática, Universidade Federal do Rio Grande do Sul, Av. Bento Gonçalves 9500, CEP 91509-900 Porto Alegre, RS, Brazil ([email protected])
Davor Dragičević
Affiliation:
Department of Mathematics, University of Rijeka, Croatia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

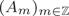Let $(A_m)_{m \in {\mathop Z}}$ be a sequence of bounded linear maps acting on an arbitrary Banach space X and admitting an exponential trichotomy and let 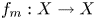$f_m:X \to X$ be a Lispchitz map for every 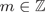$m\in {\mathop Z} $. We prove that whenever the Lipschitz constants of 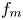$f_m$, 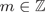$m \in {\mathop Z} $, are uniformly small, the nonautonomous dynamics given by 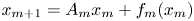$x_{m+1}=A_mx_m+f_m(x_m)$, 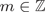$m\in {\mathop Z} $, has various types of shadowing. Moreover, if X is finite dimensional and each 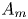$A_m$ is invertible we prove that a converse result is also true. Furthermore, we get similar results for one-sided and continuous time dynamics. As applications of our results, we study the Hyers–Ulam stability for certain difference equations and we obtain a very general version of the Grobman–Hartman's theorem for nonautonomous dynamics.

Keywords

ShadowingNonautonomus systemsExponential trichotomiesNonlinear perturbationsHyers–Ulam stability

MSC classification

Primary: 37C50: Approximate trajectories (pseudotrajectories, shadowing, etc.) 34D09: Dichotomy, trichotomy
Secondary: 34D10: Perturbations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 3 , June 2021 , pp. 863 - 884
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alonso, A. I., Hong, J. and Obaya, R.. Exponential dichotomy and trichotomy for difference equations. Comput. Math. Appl. 38 (1999), 41–49.CrossRefGoogle Scholar
2Anosov, D.. On a class of invariant sets of smooth dynamical systems (in Russian). Proc. 5th Int. Conf. Nonlinear Oscill. 2. Kiev (1970), 39–45.Google Scholar
3Backes, L. and Dragičević, D.. Shadowing for nonautonomous dynamics. Adv. Nonlinear Stud. 19 (2019), 425–436.CrossRefGoogle Scholar
4Barbu, D., Buse, C. and Tabassum, A.. Hyers–Ulam stability and discrete dichotomy. J. Math. Anal. Appl. 423 (2015), 1738–1752.CrossRefGoogle Scholar
5Bernardes, N. Jr., Cirilo, P. R., Darji, U. B., Messaoudi, A. and Pujals, E. R.. Expansivity and shadowing in linear dynamics. J. Math. Anal. Appl. 461 (2018), 796–816.CrossRefGoogle Scholar
6Bowen, R.. Equilibrium states and the ergodic theory of anosov diffeomorphisms. Lecture Notes in Mathematics, vol. 470 (Berlin, Heidelberg: Springer-Verlag, 1975).CrossRefGoogle Scholar
7Buse, C., Lupulescu, V. and O'Regan, D.. Hyers–Ulam stability for equations with differences and differential equations with time-dependent and periodic coefficients. Proc. R. Soc. Edinburgh Sect. A (to appear). https://doi.org/10.1017/prm.2019.12CrossRefGoogle Scholar
8Buse, C., O'Regan, D., Saierli, O. and Tabassum, A.. Hyers–Ulam stability and discrete dichotomy for difference periodic systems. Bull. Sci. Math. 140 (2016), 908–934.CrossRefGoogle Scholar
9Chow, S. N., Lin, X. B. and Palmer, K. J.. A shadowing lemma with applications to semilinear parabolic equations. SIAM J. Math. Anal. 20 (1989), 547–557.CrossRefGoogle Scholar
10Coppel, W. A.. Dichotomies in stability theory (Berlin, Heidelberg, New-York: Springer Verlag, 1978).CrossRefGoogle Scholar
11Dragičević, D.. Admissibility, a general type of Lipschitz shadowing and structural stability. Commun. Pure Appl. Anal. 14 (2015), 861–880.CrossRefGoogle Scholar
12Elaydi, S. and Hajek, O.. Exponential trichotomy of differential systems. J. Math. Anal. Appl. 129 (1988), 362–374.CrossRefGoogle Scholar
13Hartman, P.. On local homeomorphisms of Euclidean spaces. Bol. Soc. Mat. Mex. 5 (1960), 220–241.Google Scholar
14Henry, D. B.. Exponential dichotomies, the shadowing lemma and homoclinic orbits in Banach spaces. Resenhas 1 (1994), 381–401.Google Scholar
15Henry, D.. Geometric theory of semilinear parabolic equations. Lecture Notes in Mathematics, vol. 840 (Berlin-New York: Springer-Verlag, 1981).CrossRefGoogle Scholar
16Huy, N. T. and Minh, N. V.. Exponential dichotomy of difference equations and applications to evolution equations on the half-line. Comput. Math. Appl. 42 (2001), 301–311.CrossRefGoogle Scholar
17Meyer, K. R. and Sell, G. R.. An analytic proof of the shadowing lemma. Funkc. Ekvac. 30 (1987), 127–133.Google Scholar
18Palmer, K.. A generalization of Hartman's linearization theorem. J. Math. Anal. Appl. 41 (1973), 753–758.CrossRefGoogle Scholar
19Palmer, K. J.. Exponential dichotomies, the shadowing lemma, and transversal homoclinic points. Dyn. Rep. 1 (1988), 266–305.Google Scholar
20Palmer, K. J.. Shadowing and silnikov chaos. Nonlinear Anal. 27 (1996), 1075–1093.CrossRefGoogle Scholar
21Palmer, K.. Shadowing in dynamical systems. Theory and applications (Dordrecht: Kluwer, 2000).CrossRefGoogle Scholar
22Papaschinopoulos, G.. On exponential trichotomy of linear difference equations. Appl. Anal. 40 (1991), 89–109.CrossRefGoogle Scholar
23Perron, O.. Die stabilitätsfrage bei differentialgleichungen. Math. Z. 32 (1930), 703–728.CrossRefGoogle Scholar
24Pilyugin, S. Yu.. Shadowing in dynamical systems. Lecture Notes in Mathematics, vol. 1706 (Berlin: Springer-Verlag, 1999).Google Scholar
25Pilyugin, S. Yu. and Tikhomirov, S.. On lipschitz shadowing and structural stability. Nonlinearity 23 (2010), 2509–2515.CrossRefGoogle Scholar
26Poincaré, J. H.. Sur le problème des trois corps et les équations de la dynamique. Divergence des séries de M. Lindstedt. Acta Math. 13 (1890), 1–270.Google Scholar
27Potzsche, C.. Corrigendum on: a note on the dichotomy spectrum. J. Differ. Equation Appl. 18 (2012), 1257–1261.CrossRefGoogle Scholar
28Sasu, A. L.. Exponential dichotomy and dichotomy radius for difference equations. J. Math. Anal. Appl. 344 (2008), 906–920.CrossRefGoogle Scholar
29Sasu, A. L. and Sasu, B.. Input–output admissibility and exponential trichotomy of difference equations. J. Math. Anal. Appl. 380 (2011), 17–32.CrossRefGoogle Scholar
30Sasu, A. L. and Sasu, B.. Discrete admissibility and exponential trichotomy of dynamical systems. Discrete Cont. Dyn. Syst. 34 (2014), 2929–2962.CrossRefGoogle Scholar