Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T01:43:52.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Semilinear elliptic equations in unbounded domains of Rn

Published online by Cambridge University Press:  14 November 2011

Patrizia Donato ,
Lucia Migliaccio  and
Rosanna Schianchi
Patrizia Donato
Affiliation:
Istituto di Scienze dell'Informazione, Università di Salerno
Lucia Migliaccio
Affiliation:
Istituto di Matematica, Universita di Napoli, Italy
Rosanna Schianchi
Affiliation:
Istituto di Matematica, Universita di Napoli, Italy
Get access Rights & Permissions [Opens in a new window]

Synopsis

We study, in unbounded domains Ω⊂Rn, an elliptic semilinear problem with homogeneous boundary conditions. We assume that the nonlinear term f(x, u, Du) satisfies some condition of quadratic growth with respect to Du. We prove, in the framework of weighted Sobolev spaces, that, if 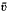and 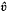are respectively a subsolution and a supersolution of our problem, then there exists a least solution ū and a greatest solution û in the ordered interval 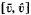and we obtain some multiplicity results.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 88 , Issue 1-2 , 1981 , pp. 109 - 119
Copyright
Copyright © Royal Society of Edinburgh 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adams, R. A.. Sobolev spaces (London: Academic Press, 1971).Google Scholar
2Agmon, S.. The Lp approach to the Dirichlet problem I. Ann. Scuola Norm. Sup. Pisa 13 (1959), 405–448.Google Scholar
3Agmon, S.. On the eigenfunction and on the eigenvalues of general elliptic boundary value problems. Comm. Pure Appl Math. 15 (1962), 119–147.CrossRefGoogle Scholar
4Amann, H.. Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces. SIAM Rev. 18 (1976), 620–709.CrossRefGoogle Scholar
5Amann, H.. Existence and multiplicity theorems for semilinear elliptic value problems. Math. Z. 150 (1976) 281–295.CrossRefGoogle Scholar
6Amann, H.. Nonlinear operators in ordered Banach spaces and some appications to nonlinear boundary value problems. In Nonlinear operators and the calculus of the variations. Lecture Notes in Mathematics 573 (Berlin: Springer, 1976).Google Scholar
7Amann, H. and Crandall, M. G.. On the existence theorems for semilinear elliptic equations. Indiana Univ. Math. J. 27 (1978), 779–790.CrossRefGoogle Scholar
8Benci, V. and Fortunate, D.Some compact embedding theorems for weighted Sobolev spaces. Boll. Un. Mat. Ital. 13B (1976), 832–843.Google Scholar
9Benci, V. and Fortunato, D.. Weighted Sobolev spaces and nonlinear Dirichlet problem in unbounded domains. Ann. Mat. Pura Appl., in press.Google Scholar
10Bony, J. M.. Principles de maximum dans les espaces de Sobolev. C. R. Acad. Sci. Paris, Ser. A 265 (1976), 333–336.Google Scholar
11Matarasso, S. and Troisi, M.. Operatori differenziali ellittici in spazi di Sobolev con peso. Ricerche Mat. 27 (1978) 1, 88–108.Google Scholar
12Protter, M. H. and Weinberger, H. F.. Maximum principles in differential equations (Englewood Cliffs, N.J.; Prentice Hall, 1967).Google Scholar
13Tomi, F.. Über semilineare elliptische Differentialgleichungen zweiter ordnung. Math. Z. 111 (1969), 350–366.CrossRefGoogle Scholar
14Troisi, M.. Teoremi di inclusione negli spazi di Sobolev con peso. Ricerche Mat. 18 (1969), 49–74.Google Scholar
15Wahl, W. V.. Über quasilineare ellptische Differentialgleichungen in der Ebene. Manuscripta Math. 8 (1973), 59–67.CrossRefGoogle Scholar