No CrossRef data available.
Published online by Cambridge University Press: 13 September 2024
In this paper, we consider the following PDE-ODE system modelling cancer invasion with slow diffusion and ECM remodelling,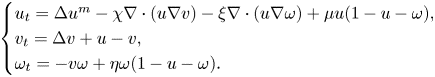
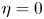 , fruitful results have been achieved since Tao and Winkler's work in 2011. However, there is no any progress for the general case $\eta >0$
, fruitful results have been achieved since Tao and Winkler's work in 2011. However, there is no any progress for the general case $\eta >0$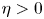 in the past ten years. In this paper, we analysed some commonly used research methods when $\eta =0$
in the past ten years. In this paper, we analysed some commonly used research methods when $\eta =0$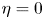 , and found that these methods are completely unsuitable for situations where $\eta >0$
, and found that these methods are completely unsuitable for situations where $\eta >0$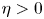 . By introducing some new forms of functionals, we reconstruct the relationship between the haptotactic term and the nonlinear diffusion term, and ultimately prove the global existence of weak solutions. This result improves and perfects a series of works previously presented in the literature.
. By introducing some new forms of functionals, we reconstruct the relationship between the haptotactic term and the nonlinear diffusion term, and ultimately prove the global existence of weak solutions. This result improves and perfects a series of works previously presented in the literature.