Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T19:13:12.544Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigid centres on the center manifold of tridimensional differential systems

Part of: Qualitative theory General theory in ordinary differential equations

Published online by Cambridge University Press:  07 September 2021

Adam Mahdi ,
Claudio Pessoa Open the ORCID record for Claudio Pessoa [Opens in a new window]  and
Jarne D. Ribeiro Open the ORCID record for Jarne D. Ribeiro [Opens in a new window]
Adam Mahdi
Affiliation:
Department of Engineering Science, Institute of Biomedical Engineering, University of Oxford, Oxford, UK ([email protected]) Faculty of Applied Mathematics, AGH University of Science and Technology, Krakw, Poland
Claudio Pessoa
Affiliation:
Departamento de Matemática, Universidade Estadual Paulista, IBILCE/UNESP, Rua Cristovão Colombo, 2265, 15.054-000, São José do Rio Preto, SP, Brazil ([email protected])
Jarne D. Ribeiro
Affiliation:
Instituto Federal de Educação, Ciência e Tecnologia do Sul de Minas Gerais, IFSULDEMINAS, Rua Mario Ribola 409, Penha II, 37903-358, Passos, MG, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the definition of rigid centres for planar differential systems, we introduce the study of rigid centres on the center manifolds of differential systems on 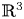$\mathbb {R}^{3}$. On the plane, these centres have been extensively studied and several interesting results have been obtained. We present results that characterize the rigid systems on 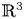$\mathbb {R}^{3}$ and solve the centre-focus problem for several families of rigid systems.

Keywords

Centre-focus problemcenter manifoldfirst integralrigid centre

MSC classification

Primary: 34C05: Location of integral curves, singular points, limit cycles
Secondary: 34A34: Nonlinear equations and systems, general
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 4 , August 2022 , pp. 1058 - 1080
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Algaba, A. and Reyes, M.. Computing center conditions for vector fields with constant angular speed. J. Comput. Appl. Math. 154 (2003), 143–159.CrossRefGoogle Scholar
Bibikov, Y. N.. Local theory of nonlinear analytic ordinary differential equations, Lecture Notes in Mathematics, vol. 702 (New York: Gostehizdat, 1979).CrossRefGoogle Scholar
Bierstone, E.. Differentiable functions. Bol. Soc. Brasil. Mat. 11 (1980), 139–189.CrossRefGoogle Scholar
Buică, A., García, I. A. and Maza, S.. Existence of inverse Jacobi multipliers around Hopf points in $\mathbb {R}^{3}$: emphasis on the center problem. J. Diff. Equ. 252 (2011), 6324–6336.CrossRefGoogle Scholar
Chavarriga, J. and Sabatini, M.. A survey of isochronous centers. Qual. Theory Dyn. Syst. 1 (1999), 1–70.CrossRefGoogle Scholar
Christopher, C.. Invariant algebraic curves and conditions for a centre. Proc. Roy. Soc. Edinburgh 124 (1994), 1209–1229.CrossRefGoogle Scholar
Cima, A., Gasull, A. and Mañosas, F.. Centers for trigonometric Abel equations. Qual. Theory Dyn. Syst. 11 (2012), 19–37.CrossRefGoogle Scholar
Collins, C. B.. Algebraic conditions for center or a focus in some simple systems of arbitrary degree. J. Math. Anal. Appl. 195 (1995), 719–735.CrossRefGoogle Scholar
Collins, C. B.. Conditions for a center in a simple class of cubic systems. Diff. Integral Equ. 10 (1997), 333–356.Google Scholar
Conti, R.. Uniformly isochronous centers of polynomial systems in $\mathbb {R}^{3}$. Lecture Notes in Pure and Appl. Math, vol. 152 (New York: Dekker, 1994). Differential equations, dynamical system, and control science, 21–31.Google Scholar
Conti, R.. Centers of planar polynomial systems. A review. Le Matematiche. 53 (1999), 207–240.Google Scholar
Dias, F. S. and Mello, L. F.. The center-focus problem and small amplitude limit cycles in rigid systems. Discrete Contin. Dyn. Syst. 32 (2012), 1627–1637.CrossRefGoogle Scholar
Dumortier, F., Llibre, J. and Artés, J. C.. Qualitative theory of planar differential systems (New York: Springer, 2006).Google Scholar
Edneral, V. F., Mahdi, A., Romanovski, V. G. and Shafer, D.. The center problem on a center manifold in $\mathbb {R}^{3}$. Nonlinear Anal. 75 (2012), 2614–2622.CrossRefGoogle Scholar
Fowles, G. R.. Analytic mechanics, 3rd ed (New York; London: Holt, Rinehart and Winston, 1977).Google Scholar
Freire, E., Gasull, A. and Guillamon, A.. Period function for perturbed isochronous centres. Qual. Theory Dyn. Syst. 3 (2002), 275–284.CrossRefGoogle Scholar
García, I. A. and Grau, M.. A survey on the inverse integrating factor. Qual. Theory Dyn. Syst. 9 (2010), 115–166.CrossRefGoogle Scholar
García, I. A., Maza, S. and Shafer, D.. Properties of monodromic points on center manifolds in $\mathbb {R}^{3}$ via Lie symmetries. J. Dyn. Diff. Equ. 25 (2013), 981–1000.CrossRefGoogle Scholar
García, I. A., Maza, S. and Shafer, D.. Cyclicity of polynomial nondegenerate centers on center manifolds. J. Diff. Equ. 265 (2018), 5767–5808.CrossRefGoogle Scholar
García, I. A., Maza, S. and Shafer, D.. Center cyclicity of Lorenz, Chen and Lu systems. Nonlinear. Anal. 188 (2019), 362–376.CrossRefGoogle Scholar
Gasull, A., Prohens, R. and Torregrosa, J.. Limit cycles for rigid cubic systems. J. Math. Anal. Appl. 303 (2005), 391–404.CrossRefGoogle Scholar
Gasull, A. and Torregrosa, J.. Exact number of limit cycles for a family of rigid systems. Proc. Am. Math. Soc. 133 (2004), 751–758.CrossRefGoogle Scholar
Giné, J. and Valls, C.. Center problem in the center manifold for quadratic differential systems in $\mathbb {R}^{3}$. J. Symbolic Comput. 73 (2016), 250–267.CrossRefGoogle Scholar
Giné, J. and Valls, C.. The generalized polynomial Moon-Rand system. Nonlinear Anal. Real. World. Appl. 39 (2018), 411–417.CrossRefGoogle Scholar
Greuel, G. M., Pfister, G. and Schönemann, H.. Singular 3.0 A Computer Algebra System for Polynomial Computations, Centre for Computer Algebra, University of Kaiserslautern, 2005. http://www.singular.uni-kl.de/.Google Scholar
Guckenheimer, J. and Holmes, P.. Nonlinear Oscillations, Dynamical Systems and Bifurctions of Vector Fields. Second Printing, Applied Mathematical Sciences, vol. 42 (New York: Springer-Verlag, 1990).Google Scholar
Han, M. and Romanovski, V. G.. Isochronicity and normal forms of polynomial systems of odes. J. Symb. Comput. 47 (2012), 1163–1174.CrossRefGoogle Scholar
Llibre, J. and Rabanal, R.. Center conditions for a class of planar rigid polynomial differential systems. Discrete Contin. Dyn. Syst. 35 (2015), 1075–1090.CrossRefGoogle Scholar
Mahdi, A.. The center problem for the third-order ODEs. Int. J. Bifur. Chaos Appl. Sci. Eng. 23 (2013), 1350078.CrossRefGoogle Scholar
Mahdi, A., Pessoa, C. and Hauenstein, J. D.. A hybrid symbolic-numerical approach to the center-focus problem. J. Symbolic Comput. 82 (2017), 57–73.CrossRefGoogle Scholar
Mahdi, A., Pessoa, C. and Shafer, D.. Centers on center manifolds in the Lu system. Phys. Lett. A 375 (2011), 3509–3511.CrossRefGoogle Scholar
Mahdi, A., Romanovski, V. G. and Shafer, D.. Stability and periodic oscillations in the Moon-Rand systems. Nonlinear Anal. Real World Appl. 14 (2013), 294–313.CrossRefGoogle Scholar
Maplesoft, a division of Waterloo Maple Inc. Maple, Version 2020, Waterloo, ON Canada, 1996–2020. https://www.maplesoft.com/.Google Scholar
Romanovski, V. G., Chen, X. and Hu, Z.. Linearizability of linear systems perturbed by fifth degree homogeneous polynomials. J. Phys. A 40 (2007), 5905–5919.CrossRefGoogle Scholar
Romanovski, V. G. and Prešern, M.. An approach to solving systems of polynomials via modular arithmetics with applications. J. Comput. Appl. Math. 236 (2011), 196–208.CrossRefGoogle Scholar
Romanovski, V. G. and Shafer, D.. The center and cyclicity problems: a computational algebra approach (Boston, MA: Birkhäuser Boston Inc., 2009).Google Scholar
Wolfram Research, Inc. Mathematica, Version 12.2, Champaign, IL, 2020, https://www.wolfram.com/mathematica.Google Scholar