Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T09:19:16.361Z Has data issue: false hasContentIssue false
  • English
  • Français

A remark on the resonance set for a semilinear elliptic equation*

Published online by Cambridge University Press:  14 November 2011

Anna Maria Micheletti
Anna Maria Micheletti
Affiliation:
Istituto di Matematiche Applicate “U.Dini”, Facoltá di Ingegneria, Universitá di Pisa, Via Bonanno, 25B, 56100 Pisa, Italy
Get access Rights & Permissions [Opens in a new window]

Abstract

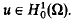We study the resonance set ∑ of pairs (α,β) ∊ ℝ2 for which the problem ∆u + αu+ − βu− = 0 has a nontrivial solution . We show that if λ0, is an eigenvalue of multiplicity two of −Δ, then 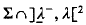has measure zero, where are the neighbouring eigenvalues of λ0. Moreover, we have that, if the operator Δ + αIu<0 + βIu < 0 has a kernel of dimension one for(α, β) ∊ ∑ and u ≠ 0 such that Δu + αu+ − βu− = 0, then (α, β) is an isolated point on ∑ ∩ L, where L is the straight line parallel to the diagonal of ℝ+ × ℝ+ through (α, β).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 4 , 1994 , pp. 803 - 809
Copyright
Copyright © Royal Society of Edinburgh 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Amann, H. and Zehender, E.. Non trivial solutions for a class of nonresonance problems and applications to nonlinear differential equations. Ann. Scuola Norm. Sup. Pisa 7 (1980), 593–603.Google Scholar
2Berger, M.. Nonlinearity and Functional Analysis (New York: Academic Press, 1977).Google Scholar
3Caffarelli, L. A. and Friedman, A.. Partial regularity of the zero set of solutions of linear and superlinear elliptic equations. J. Differential Equations 60 (1985), 420–433.CrossRefGoogle Scholar
4Dancer, E. N.. On the Dirichlet problem for weakly nonlinear partial differential equations. Proc. Roy. Soc. Edinburgh Sect. A 76 (1977), 283–300.CrossRefGoogle Scholar
5Dancer, E. N.. On the existence of solutions of certain asymptotically homogeneous problems. Math. Z. 177(1981), 33–48.CrossRefGoogle Scholar
6D'Aujourd'hui, M.. The stability of the resonance set for a problem with jumping nonlinearity. Proc. Roy. Soc. Edinburgh Sect. A 107 (1987), 201–212.CrossRefGoogle Scholar
7Gallouet, T. and Kavian, O.. Résultats d'existence et nonexistence pour certains problèmes démilinêaires à l'infini. Ann. Fac. Sci. Toulouse Math. (5) 3 (1981), 201–246.CrossRefGoogle Scholar
8Giannoni, F. and Micheletti, A. M.. Some remarks about elliptic problems with jumping nonlinearity. Rend. Mat. 7 (1987), 145–157.Google Scholar
9Ruf, B.. On nonlinear elliptic problems with jumping nonlinearities. Ann. Mat. Pura Appl. 128 (1980), 133–151.CrossRefGoogle Scholar
10Solimini, S.. Some remarks on the number of solutions of some nonlinear elliptic problems. Anal. Nonlineaire 2 (1986), 143–155.Google Scholar
11Stuart, C. A.. Elliptic boundary value problems with jumping nonlinearities (Rapport interne, Dept. de Math., Polyt. Fed. Lausanne, 1986).Google Scholar