Published online by Cambridge University Press: 12 July 2007
Let Ω be an open bounded subset of Rn and f a continuous function on Ω̄ satisfying f(x) > 0 for all x ∈ Ω̄. We consider the maximization problem for the integral ∫Ωf(x)u(x)dx over all Lipschitz continuous functions u subject to the Dirichlet boundary condition u = 0 on ∂Ω and to the gradient constraint of the form H(Du(x)) ≤ 1, and prove that the supremum is ‘achieved’ by the viscosity solution of Ĥ(Du(x)) = 1 in Ω and u = 0 on ∂Ω, where Ĥ denotes the convex envelope of H. This result is applied to an asymptotic problem, as p → ∞, for quasi-minimizers of the integral
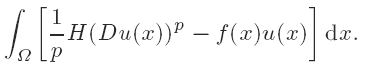 An asymptotic problem as k → ∞ for inf
An asymptotic problem as k → ∞ for inf
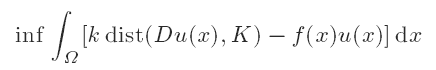 is also considered, where the infimum is taken all over
is also considered, where the infimum is taken all over 