No CrossRef data available.
Article contents
Relaxation for some dynamical problems
Published online by Cambridge University Press: 14 November 2011
Synopsis
In this article, we study the functional 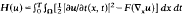 Where Ω ⊂ ĝn is a bounded open set and u: Ω ×(0, T)→ ĝm and when F: Rnm →R fails to be quasiconvex. We show that with respect to strong convergence of ∂u/∂t and weak convergence of ∇×u, the above functional behaves as
Where Ω ⊂ ĝn is a bounded open set and u: Ω ×(0, T)→ ĝm and when F: Rnm →R fails to be quasiconvex. We show that with respect to strong convergence of ∂u/∂t and weak convergence of ∇×u, the above functional behaves as 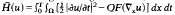 where QF is the lower quasiconvex envelope of F.
where QF is the lower quasiconvex envelope of F.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 100 , Issue 1-2 , 1985 , pp. 39 - 52
- Copyright
- Copyright © Royal Society of Edinburgh 1985
References
1Dacorogna, B.. Quasiconvexity and relaxation of non convex problems in thecalculus of variations. J. Funct. Anal. 46 (1982), 102–118.CrossRefGoogle Scholar
2Dacorogna, B.. Weak continuity and weak lower semicontinuity of nonlinear functionals. Lecture Notes in Mathematics 922 (Berlin: Springer, 1982).Google Scholar
3Perna, R. J. Di. Convergence of approximate solutions to conservation laws. Arch. Rational Mech. Anal. 82 (1983), 27–70.Google Scholar
4Ekeland, I. and Témam, R.. Analyse convexe et problèmes variationnels (Paris: Dunod, Gauthier- Villars, 1976).Google Scholar
5Morrey, C. B.. Quasiconvexity and the lower semicontinuity of multiple integrals. Pacific J. Math. 2 (1952), 25–53.CrossRefGoogle Scholar
6Morrey, C. B.. Multiple integrals in the calculus of variations (Berlin: Springer, 1966).Google Scholar
7Shearer, M.. Admissibility criteria for shock wave solutions of a system of conservations laws of mixed type. Proc. Roy. Soc. Edinburgh Sect. A 93 (1983), 233–244.CrossRefGoogle Scholar


