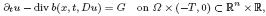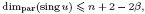Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bögelein, Verena
2014.
Global Calderón–Zygmund theory for nonlinear parabolic systems.
Calculus of Variations and Partial Differential Equations,
Vol. 51,
Issue. 3-4,
p.
555.
Scheven, Christoph
2015.
Existence of localizable solutions to nonlinear parabolic problems with irregular obstacles.
Manuscripta Mathematica,
Vol. 146,
Issue. 1-2,
p.
7.
Singer, T.
2015.
PARABOLIC EQUATIONS WITH p,q-GROWTH: THE SUBQUADRATIC CASE.
The Quarterly Journal of Mathematics,
Vol. 66,
Issue. 2,
p.
707.
Giannetti, Flavia
Passarelli di Napoli, Antonia
and
Scheven, Christoph
2016.
Higher differentiability of solutions of parabolic systems with discontinuous coefficients.
Journal of the London Mathematical Society,
Vol. 94,
Issue. 1,
p.
1.
Singer, Thomas
2016.
Existence of weak solutions of parabolic systems with p, q-growth.
manuscripta mathematica,
Vol. 151,
Issue. 1-2,
p.
87.
Baroni, Paolo
2017.
Singular parabolic equations, measures satisfying density conditions, and gradient integrability.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 153,
Issue. ,
p.
89.
Singer, Thomas
and
Vestberg, Matias
2019.
Local Hölder continuity of weak solutions to a diffusive shallow medium equation.
Nonlinear Analysis,
Vol. 185,
Issue. ,
p.
306.
Giannetti, Flavia
Passarelli di Napoli, Antonia
and
Scheven, Christoph
2020.
On higher differentiability of solutions of parabolic systems with discontinuous coefficients and (p,q)-growth.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 150,
Issue. 1,
p.
419.
Bögelein, Verena
Duzaar, Frank
Liao, Naian
and
Scheven, Christoph
2022.
Boundary regularity for parabolic systems in convex domains.
Journal of the London Mathematical Society,
Vol. 105,
Issue. 3,
p.
1702.
Bögelein, Verena
Duzaar, Frank
Liao, Naian
and
Scheven, Christoph
2022.
Gradient Hölder regularity for degenerate parabolic systems.
Nonlinear Analysis,
Vol. 225,
Issue. ,
p.
113119.
Ambrosio, Pasquale
2023.
Fractional Sobolev regularity for solutions to a strongly degenerate parabolic equation.
Forum Mathematicum,
Vol. 0,
Issue. 0,
Mons, Leon
2023.
Higher integrability for anisotropic parabolic systems of p-Laplace type.
Advances in Nonlinear Analysis,
Vol. 12,
Issue. 1,
Byun, Sun-Sig
and
Cho, Yumi
2023.
Calderón-Zygmund estimates for nonlinear parabolic equations with matrix weights on nonsmooth domains.
Journal of Differential Equations,
Vol. 371,
Issue. ,
p.
231.
Gentile, Andrea
and
Passarelli di Napoli, Antonia
2023.
Higher regularity for weak solutions to degenerate parabolic problems.
Calculus of Variations and Partial Differential Equations,
Vol. 62,
Issue. 8,
Arora, Rakesh
and
Shmarev, Sergey
2024.
Optimal global second-order regularity and improved integrability for parabolic equations with variable growth.
Advances in Nonlinear Analysis,
Vol. 13,
Issue. 1,
Ambrosio, Pasquale
and
Passarelli di Napoli, Antonia
2024.
Regularity results for a class of widely degenerate parabolic equations.
Advances in Calculus of Variations,
Vol. 17,
Issue. 3,
p.
805.
Ambrosio, Pasquale
2025.
Sharp Sobolev regularity for widely degenerate parabolic equations.
Calculus of Variations and Partial Differential Equations,
Vol. 64,
Issue. 1,