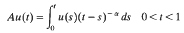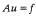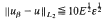Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dinh Ang, Dang
and
Gorenflo, Rudolf
1991.
Optimal Control of Partial Differential Equations.
Vol. 149,
Issue. ,
p.
26.
Ang, D. D.
Hai:, D.D.
and
Gorenflo, R.
1992.
Regularization of a generalized abel integral equation.
Applicable Analysis,
Vol. 45,
Issue. 1-4,
p.
321.
Gorenflo, R
and
Rubin, B
1994.
Locally controllable regularization of fractional derivatives.
Inverse Problems,
Vol. 10,
Issue. 4,
p.
881.
Tuan, Vu Kim
and
Gorenflo, Rudolf
1994.
On the regularization of fractional differentiation of arbitrary positive order.
Numerical Functional Analysis and Optimization,
Vol. 15,
Issue. 5-6,
p.
695.
Wang, Ping
and
Zheng, Kewang
1997.
Regularization of an Abel equation.
Integral Equations and Operator Theory,
Vol. 29,
Issue. 2,
p.
243.