Hostname: page-component-7bb8b95d7b-s9k8s Total loading time: 0 Render date: 2024-09-29T21:28:43.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Propagation of classical solutions to the perturbed wave equation in a space of odd dimension

Published online by Cambridge University Press:  14 November 2011

Gustavo Perla Menzala
Gustavo Perla Menzala
Affiliation:
Institute of Mathematics, U.F.R.J., Caixa Postal 68530, Rio de Janeiro, RJ Brasil Department of Mathematics and Division of Applied Mathematics, Brown University, Providence, RI02912, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

We prove that classical solutions of the perturbed wave equation 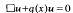in ℝn × ℝ (n = odd ≧ 3) do not satisfy Huygens' principle in the presence of symmetries. The difficulties arising from the singularities of the Riemann function (for large space dimensions) are overcome by considering a class of potentials and initial data which are radial and smooth. Our method is elementary and based on energy estimates.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 96 , Issue 3-4 , 1984 , pp. 337 - 344
Copyright
Copyright © Royal Society of Edinburgh 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bers, L., John, F. and Schechter, M.. Partial Differential Equations (New York: Interscience, 1957).Google Scholar
2Courant, R. and Hilbert, D.. Methods of Mathematical Physics, Vol. II (New York: Interscience, 1962).Google Scholar
3Glassey, R. and Strauss, W.. The scattering of certain Yang-Mills fields. Comm. Math. Phys. 89 (1983), 465–482.CrossRefGoogle Scholar
4Littman, W. and Lui, R.. Asymptotic behavior of solutions to the wave equation and other hyperbolic equations in an even number of space dimensions (to appear).Google Scholar
5Menzala, G. Perla. On the inverse problem for three-dimensional potential scattering. J. Differential Equations 20 (1) (1976), 233–247.CrossRefGoogle Scholar
6Menzala, G. Perla and Schonbek, T.. Does Huygens' principle hold for small perturbations of the wave equation? J. Differential Equations (to appear).Google Scholar
7Stellmacher, K. L.. Eine Klasse huyghenscher Differentialgleichungen und ihre Integration. Math. Ann. 130 (1955), 219–233.CrossRefGoogle Scholar