Prescribing nearly constant curvatures on balls

Luca Battaglia; Sergio Cruz-Blázquez; Angela Pistoia

doi:10.1017/prm.2023.111

Prescribing nearly constant curvatures on balls

Part of: Elliptic equations and systems Partial differential equations on manifolds; differential operators

Published online by Cambridge University Press: 27 October 2023

Luca Battaglia

Sergio Cruz-Blázquez and

Angela Pistoia

Show author details

Luca Battaglia: Affiliation:
Dipartimento di Matematica e Fisica, Università degli Studi Roma Tre, Via della Vasca Navale 84, 00146 Roma, Italy ([email protected])
Sergio Cruz-Blázquez: Affiliation:
Departamento de Análisis Matemático, Universidad de Granada, Avenida de Fuente Nueva s/n, 18071 Granada, Spain ([email protected])
Angela Pistoia: Affiliation:
Dipartimento di Scienze di Base e Applicate per l'Ingegneria, Sapienza Università di Roma, Via Antonio Scarpa 10, 00161 Roma, Italy ([email protected])

Article contents

Abstract
Introduction
Notation and preliminaries
Properties of the energy functionals
The linear theory
Existence of critical points of $\Gamma$
References

Rights & Permissions

Abstract

In this paper, we address two boundary cases of the classical Kazdan–Warner problem. More precisely, we consider the problem of prescribing the Gaussian and boundary geodesic curvature on a disk of $\mathbb {R}^2$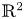, and the scalar and mean curvature on a ball in higher dimensions, via a conformal change of the metric. We deal with the case of negative interior curvature and positive boundary curvature. Using a Ljapunov–Schmidt procedure, we obtain new existence results when the prescribed functions are close to constants.

Keywords

prescribed curvature conformal metrics Ljapunov–Schmidt construction

MSC classification

Primary: 35J25: Boundary value problems for second-order elliptic equations

Secondary: 58J32: Boundary value problems on manifolds

Type: Research Article
Information: Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 36

DOI: https://doi.org/10.1017/prm.2023.111 [Opens in a new window]
Copyright: Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

1. Introduction

A classical problem arising in geometric analysis consists in prescribing certain geometric quantities on Riemannian manifolds via a conformal change of metric. It dates back to [Reference Berger9, Reference Kazdan36], where the authors proposed the following problem: given a smooth function $K$ defined on compact surface $(M^2,\,g)$, can $K$ be achieved as the Gaussian curvature of $M$ with respect to some conformal metric $\tilde g=e^ug$?

Analytically, this reduces to solve the following equation in $u$:

\begin{align*} -\Delta_g u+2k_g=2Ke^u\quad\hbox{in }M, \end{align*}

where $\Delta _g$ is the Laplace–Beltrami operator and $k_g$ denotes the Gaussian curvature of $M$ relative to $g$. Over the last few decades, this equation has received significant attention and it is not possible to give here a comprehensive list of references; a collection of results can be found in [Reference Aubin4].

If $M$ has a boundary, then boundary conditions are in order. Here we consider a non-linear boundary condition corresponding to conformally prescribing the boundary geodesic curvature $H$, for some given function $H$ defined on $\partial M$. In this case, we are led to the boundary value problem:

(1.1)\begin{equation} \left\{\begin{array}{@{}ll} -\Delta_g u+2k_g=2Ke^u & \hbox{in }M,\\ \partial_\nu u+2h_g=2He^{\frac{u}{2}} & \hbox{on }\partial M, \end{array}\right. \end{equation}

where $\nu$ is the exterior normal vector to $\partial M$ and $h_g$ its initial geodesic curvature. Equation (1.1) has been considered in particular situations; the case of constant $K$ and $H$ has been studied by Brendle in [Reference Brendle10] by means of a parabolic flow. In this situation, some classification results are available when $M$ is an annulus or the half-space, see [Reference Jiménez35, Reference Li and Zhu39, Reference Zhang47]. The case of non-constant curvatures was first addressed by Cherrier in [Reference Cherrier17], but his results are obstructed by the presence of Lagrange multipliers. Recently, the general case with $K<0$ in surfaces topologically different from the disk has been studied in [Reference López-Soriano, Malchiodi and Ruiz41], and a blow-up analysis has been performed.

Generally speaking, the case of a disk is challenging due to the non-compact nature of the conformal map group acting on it, similarly to the Nirenberg problem on ${\mathbb {S}}^2$. The problem becomes

(1.2)\begin{equation} \left\{\begin{array}{@{}ll} -\Delta u=2Ke^u & \hbox{in }{\mathbb{B}^2},\\ \partial_\nu u+2=2He^{\frac{u}{2}} & \hbox{on }{\mathbb{S}}^1, \end{array}\right. \end{equation}

Integrating (1.2) and applying the Gauss–Bonnet theorem, we obtain

\begin{align*} \int_{\mathbb{B}^2} Ke^u+\int_{{\mathbb{S}}^1}He^{\frac u2}=2\pi, \end{align*}

from which we see that $K$ or $H$ needs to be somewhere positive. Some partial results are available for the case in which one of the curvatures is zero, see [Reference Chang and Liu13, Reference Chang and Yang14, Reference Da Lio, Martinazzi and Riviére23, Reference Guo and Liu31, Reference Li and Liu38, Reference Liu and Huang40]. However, up to our knowledge, there are few results available for the case of non-constant functions $K$ and $H$. In [Reference Cruz-Blázquez and Ruiz20], the problem is posed in a new variational setting and existence of solutions in the form of global minimizers is obtained for non-negative and symmetric curvatures. Existence results for not necessarily symmetric, non-negative curvatures are found in [Reference Ruiz45] via a Leray–Schauder degree argument. In [Reference Battaglia, Medina and Pistoia6], the authors construct blowing-up solutions for (1.2) under certain non-degeneracy assumptions on $K$ and $H$ using a Ljapunov–Schmidt reduction.

Concerning the blow-up behaviour of sequences of solutions, a rather exhaustive study is given in [Reference Jevnikar, López-Soriano, Medina and Ruiz34] (see also [Reference Da Lio, Martinazzi and Riviére23, Reference Guo and Liu31]). In particular, it is shown that if $K<0$, then problem (1.2) only admits blow-ups at boundary points where the scaling-invariant function ${\mathfrak {D}}_2:{\mathbb {S}}^1\to \mathbb {R}$ defined as

(1.3)\begin{equation} {\mathfrak{D}}_2=\frac{H}{\sqrt{-K}} \end{equation}

is greater or equal than one (see [Reference Jevnikar, López-Soriano, Medina and Ruiz34, Theorem 1.1] and [Reference López-Soriano, Malchiodi and Ruiz41, Theorem 1.4]).

The natural analogue of this question in higher dimensions is the prescription of the scalar curvature of a manifold and the mean curvature of the boundary, and has received more attention.

More precisely, if $(M^n,\,g)$ is a Riemannian manifold of dimension $n\ge 3$ with boundary, and $K:\overline M\to \mathbb {R},\,H:\partial M\to \mathbb {R}$ are given smooth functions, it consists of finding positive solution for the boundary problem

(1.4)\begin{equation} \left\{\begin{array}{@{}ll}-\dfrac{4(n-1)}{n-2}\Delta_g u+k_gu=K u^{\frac{n+2}{n-2}} & \hbox{in } M,\\ \dfrac2{n-2}\partial_\nu u+h_g u=Hu^{\frac{n}{n-2}} & \hbox{on }\partial M.\end{array}\right. \end{equation}

Here $k_g$ and $h_g$ denote the scalar and boundary mean curvatures of $M$ with respect to $g$. If $u>0$ solves (1.4), then the metric $\tilde g=u^\frac 4{n-2}g$ satisfies $k_{\tilde g}=K$ and $h_{\tilde g}=H$.

In the literature, we can find many partial results for this equation. The case of prescribing a scalar flat metric with constant boundary mean curvature is known as the Escobar problem, in strong analogy with the Yamabe problem. Its study was initiated by Escobar in [Reference Escobar25, Reference Escobar26, Reference Escobar and García28], with later contributions in [Reference Almaraz2, Reference Marques42–Reference Mayer and Ndiaye44]. Different settings with constant curvatures are considered in [Reference Brendle and Chen11, Reference Chen, Ruan and Sun16, Reference Escobar27, Reference Han and Li32, Reference Han and Li33]. Some results are available for the case of non-constant functions when one of them is equal to zero. Existence results for the scalar flat problem are given in [Reference Abdelhedi, Chtioui and Ahmedou1, Reference Chang, Xu and Yang12, Reference Djadli, Malchiodi and Ahmedou24, Reference Xu and Zhang46], while the works [Reference Ben Ayed, El Mehdi and Ahmedou7, Reference Ben Ayed, El Mehdi and Ahmedou8, Reference Li37] concern the case with minimal boundaries.

On the other hand, the problem with non-constant functions $K$ and $H$ has received comparatively little study. In this regard, we highlight [Reference Ambrosetti, Li and Malchiodi3], which contains perturbative results about nearly constant positive curvature functions on the unit ball of $\mathbb {R}^n$.

The case of non-constant $K>0$ and $H$ of arbitrary sign was also considered in [Reference Djadli, Malchiodi and Ahmedou22] in the half sphere of $\mathbb {R}^3$, and a blow-up analysis was carried out. As for negative $K$, in [Reference Chen, Ho and Sun15] the authors study equation (1.4) with $K<0$ and $H<0$ by means of a geometric flow, in the spirit of [Reference Brendle10], but solutions are obtained up to Lagrange multipliers. Finally, in the recent work [Reference Cruz-Blázquez, Malchiodi and Ruiz19], the case with non-constant functions $K<0$ and $H$ of arbitrary sign is treated on manifolds of non-positive Yamabe invariant. Similarly to the two-dimensional case, it is shown that the nature of the problem changes greatly depending on whether the function ${\mathfrak {D}}_n:\partial M\to \mathbb {R}$ given by

(1.5)\begin{equation} {\mathfrak{D}}_n=\sqrt{n(n-1)}\frac{H}{\sqrt{-K}} \end{equation}

is less than one over the entire boundary or not. When ${\mathfrak {D}}_n<1$ the energy functional becomes coercive and a global minimizer can be found. However, if ${\mathfrak {D}}_n\ge 1$ somewhere on $\partial M$, a min–max argument and a careful blow-up analysis are needed to recover the existence of solutions, although only in dimension three.

In this paper, we will focus on the following perturbative version of (1.2) and (1.4):

(P ²_ε)\begin{align*} \left\{\begin{array}{@{}ll} -\Delta u={-}2(1+\varepsilon K(x))e^u & \hbox{in }{\mathbb{B}^2},\\ \partial_\nu u+2=2{\mathfrak{D}}_2(1+\varepsilon H(x))e^{\frac{u}{2}} & \hbox{on }{\mathbb{S}}^1, \end{array}\right. \end{align*}

and if $n\ge 3$

(P ⁿ_ε)\begin{align*} \left\{\begin{array}{@{}ll}-\dfrac{4(n-1)}{n-2}\Delta u={-}(1+\varepsilon K)u^{\frac{n+2}{n-2}} & \hbox{in } {\mathbb{B}^n},\\ \dfrac2{n-2}\partial_\nu u+u=\dfrac{{\mathfrak{D}}_n}{\sqrt{n(n-1)}}(1+\varepsilon H)u^{\frac{n}{n-2}} & \hbox{on } {\mathbb{S}^{n-1}}, \end{array}\right. \end{align*}

where ${\mathfrak {D}}_n>1$ is defined in (1.3) and (1.5), $K:\mathbb {B}^n\to \mathbb {R},\,H:\mathbb {S}^{n-1}\to \mathbb {R}$ are smooth with bounded derivatives and the parameter $\varepsilon \in \mathbb {R}$ small.

Our main result for problem ($P^2_\varepsilon$) reads as follows:

Theorem 1.1 Assume ${\mathfrak {D}}_2\ne \frac 2{\sqrt 3},$ let $\psi :{\mathbb {S}}^1\to \mathbb {R}$ be defined by

\begin{align*} \psi(\xi):=\frac{2\pi}{\sqrt{{\mathfrak{D}}_2^2-1}}\left(\left({\mathfrak{D}}_2-\sqrt{{\mathfrak{D}}_2^2-1}\right)K(\xi)-2{\mathfrak{D}}_2H(\xi)\right) \end{align*}

and $\Phi _1:{\mathbb {S}}^1\to \mathbb {R}$ be defined by

\begin{align*} \Phi_1(\xi):=\left({\mathfrak{D}}_2-\sqrt{{\mathfrak{D}}_2^2-1}\right)\partial_\nu K(\xi)-2{\mathfrak{D}}_2(-\Delta)^\frac12H(\xi) \end{align*}

and $\Phi _m$ be defined as in definition 2.1. If one of the following holds true:

(1) For any global maximum $\xi$ of $\psi$ there exists $m=m(\xi )\ge 1$ such that $\Phi _j(\xi )=0>\Phi _m(\xi )$ for any $j< m$;
(2) For any global minimum $\xi$ of $\psi$ there exists $m=m(\xi )\ge 1$ such that $\Phi _j(\xi )=0<\Phi _m(\xi )$ for any $j< m$;
(3) For any critical point $\xi$ of $\psi$ there exists $m=m(\xi )\ge 1$ such that $\Phi _j(\xi )=0\ne \Phi _m(\xi )$ for any $j< m$, $\psi$ is Morse and
\begin{align*} \sum_{\{\xi:\nabla\psi(\xi)=0,\,\Phi_m(\xi)<0\}}({-}1)^{\operatorname{ind}_\xi\nabla\psi}\ne1; \end{align*}

then, problem ($P^2_\varepsilon$) has a solution for $|\varepsilon |$ small enough.

Our main result for problem ($P^n_\varepsilon$) reads as follows:

Theorem 1.2 Let $\psi :{\mathbb {S}^{n-1}}\to \mathbb {R}$ be defined by

\begin{align*} \psi(\xi):=\mathtt a({\mathfrak{D}}_n)K(\xi)-\mathtt b({\mathfrak{D}}_n)H(\xi), \end{align*}

with $\mathtt a({\mathfrak {D}}_n),\,\mathtt b({\mathfrak {D}}_n)$ as in (2.3), $\Phi _1:{\mathbb {S}^{n-1}}\to \mathbb {R}$ be defined by

\begin{align*} \Phi_1(\xi):=\partial_\nu K(\xi), \end{align*}

and $\Phi _m:{\mathbb {S}^{n-1}}\to \mathbb {R}$ be defined as in definition 2.1. If one of the following holds true:

(1) For any global maximum $\xi$ of $\psi$ there exists $m=m(\xi )\ge 1$ such that $\Phi _j(\xi )=0>\Phi _m(\xi )$ for any $j< m$;
(2) For any global minimum $\xi$ of $\psi$ there exists $m=m(\xi )\ge 1$ such that $\Phi _j(\xi )=0<\Phi _m(\xi )$ for any $j< m$;
(3) For any critical point $\xi$ of $\psi$ there exists $m=m(\xi )\ge 1$ such that $\Phi _j(\xi )=0\ne \Phi _m(\xi )$ for any $j< m$, $\psi$ is Morse and
\begin{align*} \sum_{\{\xi:\nabla\psi(\xi)=0,\,\Phi_m(\xi)<0\}}({-}1)^{\operatorname{ind}_\xi\nabla\psi}\ne1; \end{align*}

then, problem ($P^2_\varepsilon$) has a solution for $|\varepsilon |$ small enough.

Problems ($P^2_\varepsilon$) and ($P^n_\varepsilon$) share many similarities, not only for their geometric importance, but also from an analytic point of view.

In fact, they both have critical terms in the interior and in the boundary non-linearities: exponential non-linearities in ($P^2_\varepsilon$) are critical in view of the Moser–Trudinger inequalities, whereas in ($P^n_\varepsilon$) we have the critical Sobolev exponent and the critical trace exponent

(1.6)\begin{equation} \frac{n+2}{n-2}={2^*}-1,\qquad\frac n{n-2}={2^\sharp}-1. \end{equation}

Moreover, since we are prescribing a negative curvature in the interior and a positive curvature in the boundary, the two non-linear terms have different signs and are therefore in competition.

Theorem 1.1 seems to be the first result of prescribing both nearly constant curvatures on a disk. Similar results were recently obtained in [Reference Battaglia, Cozzi, Fernández and Pistoia5] in the case of zero curvature in the interior and in [Reference Grossi and Prashanth30] for the sphere. Theorem 1.2 is the counterpart of the result obtained in [Reference Ambrosetti, Li and Malchiodi3], where the authors perturb the positive constant curvature on the unit ball of $\mathbb {R}^n$.

We also provide higher-order expansions of the reduced energy functional, which permits to consider also some cases of degenerate critical points. This is the case when the functionals $\Phi _m(\xi )$ play a role in theorems 1.1 and 1.2.

Such expansions require sharper estimates (see proposition 3.4 and appendix A) and both derivatives of $K,\,H$ and non-local terms appear. In particular, non-local terms are present only if the order of the expansion is high enough, depending on the dimension. At the first order, we only get the fractional Laplacian in the two-dimensional case, which is why $\Phi _1(\xi )$ is defined differently in theorems 1.1 and 1.2.

The definition of $\Phi _m$ for $m\ge 2$ is rather involved and it is therefore postponed to definition 2.1.

Finally, we point out that, in theorem 1.1, $\Phi _1$ can be seen as the normal derivative (up to a constant) of the functional $\psi$, which can be naturally extended from the circle to the closed disk. More precisely, for $\xi \in \overline {\mathbb {B}^2}$, we set

\begin{align*} \Psi(\xi):=\frac{2\pi}{\sqrt{{\mathfrak{D}}_2^2-1}}\left({\mathfrak{D}}_2-\sqrt{{\mathfrak{D}}_2^2-1}\right)K(\xi)-2{\mathfrak{D}}_2\hat H(\xi)\quad\hbox{where}\ \left\{\begin{array}{@{}ll@{}}\Delta\hat H=0 & \hbox{in }{\mathbb{B}^2}\\ \hat H=H & \hbox{in }{\mathbb{S}}^1\end{array}\right.; \end{align*}

therefore, in view of the Dirichlet-to-Neumann characterization of the fractional Laplacian, we have $\Phi _1(\xi )=\partial _\nu \Psi (\xi )$ for any $\xi \in {\mathbb {S}}^1$.

Quite interestingly, this fact has no higher-dimensional counterpart in theorem 1.2.

The assumption ${\mathfrak {D}}_2\not =\frac 2{\sqrt 3}$ (i.e. $\alpha _{\mathfrak {D}}\not =0$ in proposition 4.3) allows to apply the degree argument to the function which also depend on the extra parameter that only appears in the 2D case (see (2) of proposition 4.3). It would be interesting to understand whether this is a mere technical assumption or not and also whether it has some geometrical meaning.

The plan of the paper is as follows.

In § 2, we introduce some notation and preliminaries which we will use in the following; in § 3, we study the energy functional associated to the system and show some of its crucial properties; in § 4, we apply the Ljapunov–Schmidt finite dimensional reduction; in § 5, we study the existence of critical points to the reduced energy functional; finally, in the appendix, we prove some crucial asymptotic estimates.

2. Notation and preliminaries

We remind that ${\mathbb {B}^n}$ will denote the unit ball of $\mathbb {R}^n$, for $n\ge 2$. We consider the well-known inversion map $\mathscr {I}:\mathbb {R}^n_+\to {\mathbb {B}^n}$ defined by

(2.1)\begin{equation} \mathscr{I}(\bar x,x_n)=\left(\frac{2\bar x}{\left\vert \bar x\right\vert^2+(x_n+1)^2},\frac{1-\left\vert \bar x\right\vert^2-x_n^2}{\left\vert \bar x\right\vert^2+(x_n+1)^2}\right),\quad(\bar x,x_n)\in\mathbb{R}^{n-1}\times\mathbb{R}_+. \end{equation}

Straightforward computations show that $\mathscr {I}\circ \mathscr {I}=\hbox {Id}$, therefore $\mathscr {I}^{-1}$ has the same expression. For more details about this map, see for instance [Reference Escobar and García28], Section 2.

We point out that, up to the sign of the last coordinate, $\mathscr {I}$ extends the stereographic projection from $\partial \mathbb {R}^n_+$ to ${\mathbb {S}^{n-1}}$ and, in dimension $2$, it coincides with the Riemann map from the half-plane to the disk. In particular, $\mathscr {I}$ is a conformal map and satisfies

\begin{align*} \mathscr{I}^\star g_{{\mathbb{B}^n}}=\varrho\left\vert {\rm d}x\right\vert^2,\quad\varrho(\bar x,x_n)=\frac{4}{\left(\left\vert \bar x\right\vert^2+(x_n+1)^2\right)^2}. \end{align*}

For convenience, we define $\rho :\mathbb {R}^n_+\to \mathbb {R}_+$ by

\begin{align*} \rho=\left\{\begin{array}{@{}ll} \varrho^{\frac{n-2}{4}} & \hbox{if } n\ge3,\\ \log\varrho & \hbox{if } n=2. \end{array}\right. \end{align*}

We point out that $\rho$ satisfies (1.1) or (1.4) for some particular choices of the curvatures. More precisely, in dimension $n=2$

(2.2)\begin{equation} \left\{\begin{array}{@{}ll} -\Delta\rho=0 & \hbox{in }\mathbb{R}^2_+\\ \partial_\nu\rho=2e^{\frac{\rho}{2}} & \hbox{on }\partial\mathbb{R}^2_+, \end{array}\right. \end{equation}

while in dimensions $n\ge 3$

\begin{align*} \left\{\begin{array}{@{}ll}-\dfrac{4(n-1)}{n-2}\Delta\rho=0 & \hbox{in }\mathbb{R}^n_+,\\ \dfrac2{n-2}\partial_\nu\rho=\rho^{\frac{n}{n-2}} & \hbox{on }\partial\mathbb{R}^n_+. \end{array}\right. \end{align*}

For the reader's convenience, we collect here all the constants that appear in our computations. In the following, we agree that ${\mathfrak {D}}={\mathfrak {D}}_n$.

Definition 2.1 Let $n\ge 2$ and ${\mathfrak {D}}>1$. We define

\begin{align*} \Lambda_n& =\left\{\begin{array}{@{}ll}4 & \hbox{if}\quad n=2\\4n(n-1) & \hbox{if}\quad n\ge3\end{array}\right.,\\ \alpha_n& =\left\{\begin{array}{@{}ll}2 & \hbox{if}\quad n=2\\ \dfrac{(n-2)^2}{8n(n-1)} & \textit{if}\quad n\ge3\end{array}\right.,\\ \beta_n& =\left\{\begin{array}{@{}ll}2 & \hbox{if}\quad n=2\\2\sqrt{\dfrac n{n-1}} & \textit{if}\quad n\ge3\end{array}\right.,\\ a_{n,i,j}& =\Lambda_n^\frac n2\int_{\mathbb{R}^n_+}\frac{|\bar y|^{2i}y_n^j}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y{\rm d}y_n,\\ b_{n,j}& =\Lambda_n^\frac{n-1}2\beta_n\frac{\mathfrak{D}}{\left({\mathfrak{D}}^2-1\right)^\frac{n-2j-1}2}\int_{\partial\mathbb{R}^n_+}\frac{|\bar y|^{2j}}{\left(\left\vert \bar y\right\vert^2+1\right)^{n-1}}{\rm d}\bar y,\\ c_{n,m}& =\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}}\left({\mathfrak{D}}^2-1\right)^\frac{m-n+1}2\\ & \quad \times \int_{\partial\mathbb{R}^n_+}|\bar y|^m\left(\frac1{\left(|\bar y|^2+1\right)^{n-1}}-\sum_{j=0}^\frac{m-n}2({-}1)^j\frac{(n+j-2)!}{j!(n-2)!}\frac1{|\bar y|^{2(n+j-1)}}\right){\rm d}\bar y,\\ d_{n,j}& =\Lambda_n^\frac n2\omega_{n-2}\int_0^\pi\sin^jt{\rm d}t\\ e_n& =\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}}\omega_{n-2}\\ A_{n,i,j}& =\frac1{(j-2i)!(2i)!}\frac{(n-3)!!}{(2i)!!(n+2i-3)!!},\\ B_{n,j}& =\frac{(n-3)!!}{(2j)!(2j)!!(n+2j-3)!!},\\ C_{n,m,i}& =\frac{(m-i-1)!}{(n-1)!i!(m-n-2i)!}({\mathfrak{D}}^2-1)^i{\mathfrak{D}}^{m-n-2i}\\ D_{n,m}& =\frac{\left(\frac{n+m+1}2-2\right)!}{\left(\frac{m-n+1}2\right)!(n-2)!}\left({\mathfrak{D}}^2-1\right)^\frac{m-n+1}2 \\ \mathsf I_{n,m,i}(K)& =\Lambda_n^\frac n2\\ & \quad \times \int_{\mathbb{B}^n}\!\left(\!K(z)\,{-}\sum_{|\alpha|\le m}\frac1{|\alpha|!}\partial_{\xi_\alpha}K(\xi)(z\,{-}\,\xi)^\alpha\!\right)\frac{|z\,{+}\,\xi|^{2i}\left(1\,{-}\,|z|^2\right)^{m-n-2i}}{|z-\xi|^{2m}}{\rm d}z\\ \mathsf J_{n,m}(H)& =\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}}\\ & \quad \times \int_{{\mathbb{S}^{n-1}}}\left(H(z)-\sum_{|\alpha|\le m-1}\frac1{|\alpha|!}\partial_{\xi_\alpha}H(\xi)(z-\xi)^\alpha\right)\frac{|z+\xi|^{m-n+1}}{|z-\xi|^{n+m-1}}{\rm d}z \end{align*}

In particular, set

(2.3)\begin{equation} \begin{aligned} & \mathtt a({\mathfrak{D}}_n):=a_{n,0,0}=\Lambda_n^\frac n2\int_{\mathbb{R}^n_+}\frac{1}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}}_n)^2-1\right)^n}{\rm d}\bar y{\rm d}y_n,\\ & \mathtt b({\mathfrak{D}}_n):=b_{n,0}=\Lambda_n^\frac{n-1}2\beta_n\frac{{\mathfrak{D}}_n}{\left({\mathfrak{D}}_n^2-1\right)^\frac{n-1}2}\int_{\partial\mathbb{R}^n_+}\frac{1}{\left(\left\vert \bar y\right\vert^2+1\right)^{n-1}}{\rm d}\bar y. \end{aligned} \end{equation}

We define the functionals $\Phi _j(\xi )$ as follows.

For $j\le n-2$ we set:

\begin{align*} & \Phi_j(\xi)\\& \quad :=\left\{\begin{array}{@{}ll}(1+\xi)^j\left(-\sum_{i=0}^{\frac j2}a_{n,i,j}A_{n,i,j}\partial_\nu^{j-2i}\Delta_\tau^iK(\xi)+b_{n,j}B_{n,j}\Delta^jK(\xi)\right) & \hbox{if }j\hbox{ even}\\ (1+\xi)^j\sum_{i=0}^{\frac{j-1}2}a_{n,i,j}A_{n,i,j}\partial_\nu^{j-2i}\Delta_\tau^iK(\xi) & \hbox{if }j\hbox{ odd} \end{array}\right. \end{align*}

For $j=n-1,\,n$ we set:

\begin{align*} \Phi_{n-1}(\xi)& :=\left\{\begin{array}{@{}ll}0 & \hbox{if }n\hbox{ even}\\ (1+\xi_n)^{n-1}e_nB_{n,\frac{n-1}2}\Delta^{\frac{n-1}2}H(\xi) & \hbox{if }n\hbox{ odd}\end{array}\right.\\ \Phi_n(\xi)& :=(1+\xi_n)^{n-1}\\ & \quad \times \left(({-}1)^n\sum_{i=0}^{\lfloor\frac{n-1}2\rfloor}a_{n,i,n-1}A_{n,i,n-1}\partial_\nu^{n-1-2i}\Delta_\tau^iK(\xi)+\mathsf J_{n,n-1}(H)\right). \end{align*}

For $m\ge n$ we set:

\begin{align*} & \Phi_{2m-n+1}(\xi)\\ & \quad:=(1+\xi_n)^m\left(\sum_{i=0}^{\lfloor\frac{m-n}2\rfloor}\sum_{j=0}^{\lfloor\frac m2\rfloor}({-}1)^{m-n-i-1}A_{n,j,m}C_{n,m,i}d_{2m-n-2i-2j}\partial_\nu^{m-2j}\Delta_\tau^jK(\xi)\right.\\ & \qquad+\left.\left\{\begin{array}{@{}ll}0 & \hbox{if }n\hbox{ even or }m\hbox{ odd}\\ ({-}1)^{\frac{m-n+1}2}e_nB_{n,\dfrac m2}D_{n,m}\Delta^{\frac m2}H(\xi) & \hbox{if }n\hbox{ odd and }m\hbox{ even}\\ \end{array}\right.\right) \\ & \Phi_{2m-n+2}(\xi)\\& \quad :=(1+\xi_n)^m\left(\sum_{i=0}^{\lfloor\frac{m-n}2\rfloor}({-}1)^{m-n-i-1}C_{n,m,i}\mathsf I_{n,m,i}(K)\right.\\ & \qquad+\left.\left\{\begin{array}{@{}ll}c_{n,m}B_{n,\dfrac m2}\Delta^{\frac m2}H(\xi) & \hbox{if }n\hbox{ and }m\hbox{ even}\\ 0 & \hbox{if }n\hbox{ and }m\hbox{ odd}\\ ({-}1)^{\frac{m-n+1}2}D_{n,m}\mathsf{J}_{n,m}(H) & \hbox{otherwise}\end{array}\right.\right) \end{align*}

The symbol $a\lesssim b$ will be used to mean $a\le cb$ with $c$ independent on the quantities.

We denote as $\partial _\nu$ the (outer) normal derivative of a function at a point on ${\mathbb {S}^{n-1}}$ and as $\Delta _\tau$ the tangential Laplacian.

For a multi-index $\alpha =(\alpha _1,\,\dots,\,\alpha _n)\in \mathbb {N}^n$ we denote:

\begin{align*} |\alpha|:=\alpha_1+\dots+\alpha_n;\qquad\qquad x^\alpha:=x_1^{\alpha_1}\cdot\dots\cdot x_n^{\alpha_n};\qquad\qquad\partial_{x_\alpha}:=\partial_{x_1}^{\alpha_1}\dots\partial_{x_n}^{\alpha_n}. \end{align*}

2.1. Conformal metrics

Throughout this article, we will use the existing conforming equivalence between $\mathbb {R}^n_+$ and ${\mathbb {B}^n}$ via the inversion map (2.1), often without explicitly specifying it. Therefore, it is important to remember the conformal properties of the conformal Laplacian and conformal boundary operator.

If $n\ge 3$ and $\tilde g=\rho ^\frac 4{n-2}g$ is a conformal metric, then the conformal Laplacian and conformal boundary operators, defined by

\begin{align*} L_g={-}\frac{4(n-1)}{n-2}\Delta_g+k_g,\quad B_g=\frac2{n-2}\partial_\nu+h_g, \end{align*}

are conformally invariant in the following sense:

(2.4)\begin{equation} L_g\varphi=\rho^\frac{n+2}{n-2}L_{\tilde g}\left(\frac\varphi\rho\right),\quad B_g\varphi=\rho^\frac n{n-2}B_{\tilde g}\left(\frac\varphi\rho\right). \end{equation}

If $n=2$, then the Laplace–Beltrami operator and the normal derivative satisfy the following conformal property: if $\tilde g=e^\rho g$ is a conformal metric, then

\begin{align*} \Delta_{e^\rho g}=e^{-\rho}\Delta_g,\quad\nabla_{e^\rho g}\cdot\eta_{e^\rho g}=e^{-\frac\rho2}\nabla\cdot\eta_g. \end{align*}

The following result establishes the conformal invariance of a certain geometric quantity that will be very much related to our energy functionals.

Lemma 2.2 Let $(M^n,\,g)$ be a compact Riemannian manifold of dimension $n\ge 3$ and $\tilde g=\varphi ^{\frac {4}{n-2}}g$ a conformal metric with $\varphi$ smooth and positive. If we set $\hat f=f\varphi ^{-1},$ then

(2.5)\begin{align} & \frac{4(n-1)}{n-2}\int_M\left(\nabla_{\tilde g}\hat u\cdot\nabla_{\tilde g}\hat v\right){\rm d}V_{\tilde g}+\int_M k_{\tilde g}\hat u\hat v\:{\rm d}V_{\tilde g}+2(n-1)\int_{\partial M}h_{\tilde g}\hat u\hat v\:{\rm d}\sigma_{\tilde g}\nonumber\\ & \quad=\frac{4(n-1)}{n-2}\int_M\left(\nabla_gu\cdot\nabla_gv\right){\rm d}V_g+\int_Mk_guv\:{\rm d}V_g+2(n-1)\int_{\partial M}h_g uv\:{\rm d}\sigma_g. \end{align}

Proof. We will use the following basic identities:

\begin{align*} {\rm d}V_{\tilde g}=\varphi^{2^*} {\rm d}V_g, {\rm d}\sigma_{\tilde g}=\varphi^{2^\sharp} {\rm d}\sigma_g,\nabla_{\tilde g}=\varphi^{-\frac{4}{n-2}}\nabla_g, \end{align*}

where ${2^*},\,{2^\sharp }$ are as in (1.6) and the relation between $k_{\tilde g}$, $k_g$, $h_{\tilde g}$ and $h_g$ given by (1.4). The first term in the left-hand side of (2.5) can be decomposed using the previous identities:

(2.6)\begin{align} & \int_M\left(\nabla_{\tilde g}\hat u\cdot\nabla_{\tilde g}\hat v\right){\rm d}V_{\tilde g}=\int_M\varphi^2\left(\nabla_g\hat u\cdot\nabla_g\hat v\right){\rm d}V_g\nonumber\\ & \quad=\int_M\left(\nabla_gu\cdot\nabla_gv\right){\rm d}V_g-\int_M\left(\hat v\nabla_g\varphi\cdot\nabla_gu+\hat u\nabla_g\varphi\cdot\nabla_gv-\hat u\hat v\left\vert \nabla_g\varphi\right\vert^2\right){\rm d}V_g. \end{align}

On the other hand, integrating by parts on $M$ and using (1.4):

(2.7)\begin{align} & \int_Mk_{\tilde g}\hat u\hat v\:{\rm d}V_{\tilde g}=\int_M\hat u\hat v\left(k_g\varphi^2-\frac{4(n-1)}{n-2}(\Delta_g\varphi)\varphi\right){\rm d}V_g\nonumber\\ & \quad=\int_Mk_guv\:{\rm d}V_g-2(n-1)\int_{\partial M}h_{\tilde g}\hat u\hat v\varphi^{2^\sharp} {\rm d}\sigma_g+2(n-1)\int_{\partial M}h_g uv\:{\rm d}\sigma_g\nonumber\\ & \qquad+\frac{4(n-1)}{n-2}\int_M\left(\hat v\nabla_g\varphi\cdot\nabla_gu+\hat u\nabla_g\varphi\cdot\nabla_gv-\hat u\hat v\left\vert \nabla_g\varphi\right\vert^2\right){\rm d}V_g. \end{align}

Finally, (2.5) can be obtained combining (2.6) and (2.7).

2.2. Solutions of the unperturbed problems

By means of the inversion map and the classification results available for $\mathbb {R}^n_+$, we can give an $n$-dimensional family of solutions for the problems ($P^2_\varepsilon$) and ($P^n_\varepsilon$) with $\varepsilon =0$.

First, we consider the problem in ${\mathbb {B}^2}$:

(P ²₀)\begin{align*} \left\{\begin{array}{@{}ll} -\Delta u={-}2e^u & \hbox{in }{\mathbb{B}^2}\\ \partial_\nu u+2=2{\mathfrak{D}} e^{\frac{u}{2}} & \hbox{on }{\mathbb{S}}^1. \end{array}\right. \end{align*}

By [Reference Zhang47], a family of solutions of the problem in the half space

(2.8)\begin{equation} \left\{\begin{array}{@{}ll} -\Delta u={-}2e^u & \hbox{in }\mathbb{R}^2_+\\ \partial_\nu u=2{\mathfrak{D}} e^{\frac{u}{2}} & \hbox{on }\partial\mathbb{R}^2_+ \end{array}\right. \end{equation}

is given by

\begin{align*} U_{x_0,\lambda}(x,y)=2\log\frac{2\lambda}{(x-x_0)^2+(y+{\mathfrak{D}}\lambda)^2-\lambda^2}, \end{align*}

for $\lambda >0$ and $x_0\in \mathbb {R}$. Other classification results for solutions to (2.8) are given in [Reference Gálvez and Mira29, Reference Li and Zhu39].

Let us call $\hat U_{x_0,\lambda }=\left (U_{x_0,\lambda }-\rho \right )\circ \mathscr {I}^{-1}$. Taking into account equation (2.2) and the conformal properties of the Laplacian and normal derivative in $\mathbb {R}^2$, it is clear that

\begin{align*} \left\{\begin{array}{@{}ll} -\Delta\hat U={-}2e^{\hat U} & \hbox{in }{\mathbb{B}^2}\\ \partial_\nu\hat U+2=2{\mathfrak{D}} e^{\frac{\hat U}2} & \hbox{on }{\mathbb{S}}^1. \end{array}\right. \end{align*}

Therefore, a family of solutions for ($P^2_0$) is given by

(2.9)\begin{equation} \hat U_{x_0,\lambda}(s,t)=2\log\frac{\lambda\left(x^2+(y+1)^2\right)}{(x-x_0)^2+(y+{\mathfrak{D}}\lambda)^2-\lambda^2}, \end{equation}

with

\begin{align*} x=x(s,t)=\frac{2s}{s^2+(t+1)^2},\quad y=y(s,t)=\frac{1-s^2-t^2}{s^2+(t+1)^2}, \end{align*}

$\lambda >0$ and $x_0\in \mathbb {R}.$

Now, we address the unperturbed problem in ${\mathbb {B}^n}$ for $n\ge 3$:

(P ⁿ₀ʹ)\begin{align*} \left\{\begin{array}{@{}ll}-\dfrac{4(n-1)}{n-2}\Delta u={-}u^{\frac{n+2}{n-2}} & \hbox{in }{\mathbb{B}^n},\\ \dfrac2{n-2}\partial_\nu u+u=\frac{{\mathfrak{D}}}{\sqrt{n(n-1)}}u^{\frac{n}{n-2}} & \hbox{on }{\mathbb{S}^{n-1}}. \end{array}\right. \end{align*}

Consider $\mathbb {R}^n_+$ with its usual metric, and the problem

(2.10)\begin{equation} \left\{\begin{array}{@{}ll}\dfrac{-4(n-1)}{n-2}\Delta u={-}u^{\frac{n+2}{n-2}} & \hbox{in }\mathbb{R}^n_+,\\ - \dfrac2{n-2}\partial_{x_n}u=\frac{{\mathfrak{D}}}{\sqrt{n(n-1)}}u^{\frac{n}{n-2}} & \hbox{on }\partial\mathbb{R}^n_+. \end{array}\right. \end{equation}

The results in [Reference Chipot, Fila and Shafrir18] imply that all solutions of (2.10) have the form

\begin{align*} U_{x_0,\lambda}(\bar x,x_n)=\frac{(4n(n-1))^\frac{n-2}4\lambda^\frac{n-2}2}{(\left\vert \bar x-x_0\right\vert^2+(x_n+\lambda{\mathfrak{D}})^2-\lambda^2)^\frac{n-2}2}, \end{align*}

for any $x_0\in \partial \mathbb {R}^n_+$ and $\lambda >0$.

Then, by (2.4), we can write (2.10) as:

\begin{align*} \left\{\begin{array}{@{}ll} \rho^{\frac{n+2}{n-2}}\dfrac{-4(n-1)}{n-2}\Delta\left(\dfrac u\rho\right)={-}u^{\frac{n+2}{n-2}} & \hbox{in }\mathbb{R}^n_+,\\ \rho^{\frac{n}{n-2}}\left(\dfrac2{n-2}\partial_\nu\left(\dfrac u\rho\right)+\left(\dfrac u\rho\right)\right)=\frac{{\mathfrak{D}}}{\sqrt{n(n-1)}}u^{\frac{n}{n-2}} & \hbox{on }\partial\mathbb{R}^n_+. \end{array}\right. \end{align*}

If we call $\hat u=\left (\frac u\rho \right )\circ \mathscr {I}^{-1}$, it is clear that

\begin{align*} \left\{\begin{array}{@{}ll} \dfrac{-4(n-1)}{n-2}\Delta\hat u={-}{\hat u}^{\frac{n+2}{n-2}} & \hbox{in }{\mathbb{B}^n},\\ \dfrac2{n-2}\partial_\nu\hat u+\hat u=\frac{{\mathfrak{D}}}{\sqrt{n(n-1)}}{\hat u}^{\frac{n}{n-2}} & \hbox{on }{\mathbb{S}^{n-1}}, \end{array}\right. \end{align*}

which is exactly ($P^{n\,'}_0$). Hence, a family of solutions of ($P^{n\,'}_0$) is given by

(2.11)\begin{equation} \hat U_{x_0,\lambda}(\bar x,x_n)=\lambda^\frac{n-2}2(n(n-1))^\frac{n-2}4\left(\frac{\left\vert \bar z\right\vert^2+(z_n+1)^2}{\left\vert \bar z-x_0\right\vert^2+(z_n+\lambda{\mathfrak{D}})^2-\lambda^2}\right)^\frac{n-2}2, \end{equation}

with

\begin{align*} \bar z=\bar z(\bar x,x_n)=\frac{2\bar x}{\left\vert \bar x\right\vert^2+(x_n+1)^2},\quad z_n=z_n(\bar x,x_n)=\frac{1-\left\vert \bar x\right\vert^2-x_n^2}{\left\vert \bar x\right\vert^2+(x_n+1)^2}. \end{align*}

In view of formulae (2.9) and (2.11) we set:

\begin{align*} P_{x_0,\lambda}(\bar x, x_n)=\frac{\Lambda_n\lambda^2\left(\left\vert \bar z\right\vert^2+(z_n+1)^2\right)^2}{\left(\left\vert \bar z-x_0\right\vert^2+(z_n+\lambda{\mathfrak{D}})^2-\lambda^2\right)^2}, \end{align*}

with $\bar z,\,z_n$ as before, $x_0\in \mathbb {R}^{n-1}$, $\lambda >0$, and define

(2.12)\begin{equation} V_{x_0,\lambda}=\left\{\begin{array}{@{}ll} {P_{x_0,\lambda}}^{\frac{n-2}{4}} & \hbox{if}\quad n\ge3,\\ \log P_{x_0,\lambda} & \hbox{if}\quad n=2. \end{array}\right. \end{equation}

3. Properties of the energy functionals

We define the functionals $J^n_\varepsilon :H^1\left ({\mathbb {B}^n}\right )\to \mathbb {R}$ by

(3.1)\begin{align} J^2_\varepsilon(u)& =\frac12\int_{\mathbb{B}^2}\left\vert \nabla u\right\vert^2+2\int_{{\mathbb{S}}^1}u+2\int_{\mathbb{B}^2}(1+\varepsilon K)e^u-4{\mathfrak{D}}\int_{{\mathbb{S}}^1}(1+\varepsilon H)e^{\frac u2},\nonumber\\ J^n_\varepsilon(u)& =\frac12\int_{\mathbb{B}^n}\left\vert \nabla u\right\vert^2+\frac12\int_{{\mathbb{S}^{n-1}}}u^2+\frac{(n-2)^2}{8n(n-1)}\int_{\mathbb{B}^n}(1+\varepsilon K)\left\vert u\right\vert^{2^*} \end{align}

(3.2)\begin{align} & \quad-\frac{(n-2)^2}{4\sqrt{n(n-1)^3}}{\mathfrak{D}}\int_{{\mathbb{S}^{n-1}}}(1+\varepsilon H)\left\vert u\right\vert^{2^\sharp},\quad\hbox{if}\quad n\ge3. \end{align}

Observe that we can write

\begin{align*} J^n_\varepsilon(u)=J^n_0(u)+\varepsilon\alpha_n\gamma^n(u), \end{align*}

with

\begin{align*} \gamma^n(u)=\left\{\begin{array}{@{}ll}\displaystyle\int_{\mathbb{B}^2} Ke^u-\beta_2{\mathfrak{D}}\int_{{\mathbb{S}}^1}He^{\frac{u}{2}} & \hbox{if }n=2\\ \displaystyle\int_{\mathbb{B}^n} K\left\vert u\right\vert^{2^*}-\beta_n{\mathfrak{D}}\int_{{\mathbb{S}^{n-1}}}H\left\vert u\right\vert^{2^\sharp} & \hbox{if }n\ge3\end{array}\right. \end{align*}

with $\alpha _n,\,\beta _n$ as in definition 2.1.

Let $V_{x_0,\lambda }$ be given by (2.12). We set

\begin{align*} \Gamma(x_0,\lambda)=\gamma^n\left(V_{x_0,\lambda}\right)=\int_{\mathbb{B}^n} K{P_{x_0,\lambda}}^\frac n2-\beta_n{\mathfrak{D}}\int_{\mathbb{S}^{n-1}} H{P_{x_0,\lambda}}^\frac{n-1}2. \end{align*}

The first term of the energy is constant along our family of solutions:

Proposition 3.1 There exist constants $\mathtt E_{n,{\mathfrak {D}}}$, independent on $\lambda$ and $x_0$, such that

\begin{align*} J_0^n(V_{x_0,\lambda})=\mathtt E_{n,{\mathfrak{D}}},\quad\forall n\ge2. \end{align*}

Proof. Let us study the cases $n=2$ and $n\ge 3$ separately.

When $n=2$, integrating by parts and using ($P^2_0$) and (2.2), we can see that:

\begin{align*} & \frac12\int_{\mathbb{B}^2}\left\vert \nabla V_{x_0,\lambda}\right\vert^2+2\int_{{\mathbb{S}}^1}V_{x_0,\lambda}=\frac12\int_{\mathbb{R}^2_+}\left\vert \nabla\left(U_{x_0,\lambda}-\rho\right)\right\vert^2+2\int_\mathbb{R}(U_{x_0,\lambda}-\rho)e^\frac\rho2\\ & \quad={-}\frac12\int_{\mathbb{R}^2_+}\Delta U_{x_0,\lambda}(U_{x_0,\lambda}-\rho)+\frac12\int_\mathbb{R}\partial_\nu U_{x_0,\lambda}(U_{x_0,\lambda}-\rho)+2\int_\mathbb{R}(U_{x_0,\lambda}-\rho)e^\frac\rho2\\ & \quad=\frac12\int_{\mathbb{R}^2_+}\left\vert \nabla U_{x_0,\lambda}\right\vert^2+\frac12\int_{\mathbb{R}^2_+}\Delta U_{x_0,\lambda}\,\rho-\frac12\int_\mathbb{R}\partial_\nu U_{x_0,\lambda}\rho+2\int_\mathbb{R}(U_{x_0,\lambda}-\rho)e^\frac\rho2\\ & \quad=\frac12\int_{\mathbb{R}^2_+}\left\vert \nabla U_{0,1}\right\vert^2-\frac12\int_{\mathbb{R}^2_+}\left\vert \nabla\rho\right\vert^2. \end{align*}

Now,

\begin{align*} 2\int_{\mathbb{B}^2} e^{V_{x_0,\lambda}}-4{\mathfrak{D}}\int_{{\mathbb{S}}^1}e^\frac{V_{x_0,\lambda}}2=2\int_{\mathbb{R}^2_+}e^{U_{0,1}}-4{\mathfrak{D}}\int_\mathbb{R} e^\frac{U_{0,1}}2. \end{align*}

Finally,

(3.3)\begin{equation} J^2_0(V_{x_0,\lambda})=\frac12\int_{\mathbb{R}^2_+}\left(\left\vert \nabla U_{0,1}\right\vert^2-\left\vert \nabla\rho\right\vert^2\right)+2\int_{\mathbb{R}^2_+}e^{U_{0,1}}-4{\mathfrak{D}}\int_\mathbb{R} e^\frac{U_{0,1}}2. \end{equation}

As for the case $n\ge 3$, from lemma 2.2 it follows

\begin{align*} \frac12\int_{\mathbb{B}^n}\left\vert \nabla V_{x_0,\lambda}\right\vert^2+\frac12\int_{{\mathbb{S}^{n-1}}}{V_{x_0,\lambda}}^2=\frac12\int_{\mathbb{R}^n_+}\left\vert \nabla U_{x_0,\lambda}\right\vert^2=\frac12\int_{\mathbb{R}^n_+}\left\vert \nabla U_{0,1}\right\vert^2. \end{align*}

Moreover, by a direct change of variables, we obtain

\begin{align*} \int_{\mathbb{B}^n}{V_{x_0,\lambda}}^{2^*}-\beta_n{\mathfrak{D}}\int_{{\mathbb{S}^{n-1}}}{V_{x_0,\lambda}}^{2^\sharp}=\int_{\mathbb{R}^n_+}{U_{0,1}}^{2^*}-\beta_n{\mathfrak{D}}\int_{\partial\mathbb{R}^n_+}{U_{0,1}}^{2^\sharp}. \end{align*}

Therefore,

(3.4)\begin{equation} J^n_0(V_{x_0,\lambda})=\frac12\int_{\mathbb{R}^n_+}\left\vert \nabla U_{0,1}\right\vert^2+\alpha_n\left(\int_{\mathbb{R}^n_+}{U_{0,1}}^{2^*}-\beta_n{\mathfrak{D}}\int_{\partial\mathbb{R}^n_+}{U_{0,1}}^{2^\sharp}\right). \end{equation}

By a change of variables and using the relations in § 2, we can move to $\mathbb {R}^n_+$ and write our function $\Gamma$ in a more suitable way.

Proposition 3.2 It holds

(3.5)\begin{align} \Gamma(x_0,\lambda)& =\int_{\mathbb{R}^n_+}\frac{\Lambda_n^\frac n2\tilde K(\bar x,x_n)\lambda^n{\rm d}\bar x{\rm d}x_n}{\left(\left\vert \bar x-x_0\right\vert^2+(x_n+\lambda{\mathfrak{D}})^2-\lambda^2\right)^n}\nonumber\\& \quad -\int_{\partial\mathbb{R}^n_+}\frac{\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}}\tilde H(\bar x)\lambda^{n-1}{\rm d}\bar x}{\left(\left\vert \bar x-x_0\right\vert^2+\lambda^2({\mathfrak{D}}^2-1)\right)^{n-1}}\nonumber\\ & =\int_{\mathbb{R}^n_+}\frac{\Lambda_n^\frac n2\tilde K(\lambda\bar y+x_0,\lambda y_n)}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y{\rm d}y_n\nonumber\\& \quad -\int_{\partial\mathbb{R}^n_+}\frac{\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}}\tilde H(\lambda\bar y+x_0)}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y, \end{align}

where $\tilde K=K\circ \mathscr {I},\,\tilde H=H\circ \mathscr {I}$.

We are interested in the behaviour of $\Gamma$ at infinity and when $\lambda \to 0$.

Proposition 3.3 $\lim _{\left \vert x_0\right \vert +\lambda \to +\infty }\Gamma (x_0,\,\lambda )=\psi ((0,\,-1))$

Proof. First, notice that

\begin{align*} & \lim_{\lambda+\left\vert x_0\right\vert\to+\infty}\mathscr{I}(\lambda\bar x+x_0,\lambda x_n)\nonumber\\& \quad =\lim_{\lambda+\left\vert x_0\right\vert\to+\infty}\left(\frac{2(\lambda\bar x+x_0)}{\left\vert \lambda\bar x+x_0\right\vert^2+(\lambda x_n+1)^2},\frac{1-|\lambda\bar x+x_0|^2-(\lambda x_n)^2}{\left\vert \lambda\bar x+x_0\right\vert^2+(\lambda x_n+1)^2}\right)\\ & \quad =\left\{\begin{array}{@{}ll} (0,-1) & \hbox{locally uniformly on}\quad(\bar x,x_n)\neq(0,0),\\ \mathscr{I}(x_0,0) & \hbox{if}\quad(\bar x,x_n)=(0,0). \end{array}\right. \end{align*}

With that in mind, we fix $\varepsilon >0$ small enough and write

\begin{align*} \Gamma(x_0,\lambda)& =\int_{|y|>\epsilon}\frac{\Lambda_n^\frac n2\tilde K(\lambda\bar y+x_0,\lambda y_n)}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y{\rm d}y_n\\& \quad -\int_{|\bar y|>\epsilon}\frac{\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}}\tilde H(\lambda\bar y+x_0,0)}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y\\ & \quad+ \int_{|y|\le\epsilon}\frac{\Lambda_n^\frac n2\tilde K(\lambda\bar y+x_0,\lambda y_n)}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y{\rm d}y_n\\& \quad -\int_{|\bar y|\le\epsilon}\frac{\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}}\tilde H(\lambda\bar y+x_0,0)}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y. \end{align*}

Then, taking limits when $\lambda +\left \vert x_0\right \vert \to +\infty$,

\begin{align*} \Gamma(x_0,\lambda)& = K(0,-1)\int_{|y|>\epsilon}\frac{\Lambda_n^\frac n2{\rm d}\bar y{\rm d}y_n}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}\\ & \quad-H(0,-1)\int_{|\bar y|\le\epsilon}\frac{\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}} {\rm d}\bar y}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}+O\left(\epsilon^{n-1}\right)\\ & \quad+ K(\mathscr{I}(x_0,0))O\left(\epsilon^n\right)-H(\mathscr{I}(x_0,0))O\left(\epsilon^{n-1}\right). \end{align*}

The claim follows from taking limits when $\epsilon \to 0$.

The following result describes the behaviour of $\Gamma$ around $\lambda =0$. Its proof will be postponed to appendix A.

Proposition 3.4 Define $\psi :{\mathbb {S}^{n-1}}\to \mathbb {R}$ by $\psi (\xi ):=\mathtt a({\mathfrak {D}}_n)K(\xi )-\mathtt b({\mathfrak {D}}_n)H(\xi )$, and let us write $\xi =\mathscr {I}(x_0)\in {\mathbb {S}^{n-1}}$. The following expansions hold, for any $m\in \mathbb {N}$, when $\lambda \ll 1$:

If $n=2$,

\begin{align*} \Gamma(x_0,\lambda)& =\psi(\xi)-\left(\vphantom{\frac1\lambda}2\pi(1+\xi_n)\lambda\left(\left({\mathfrak{D}}-\sqrt{{\mathfrak{D}}^2-1}\right)\,\partial_\nu K(\xi)-2{\mathfrak{D}}(-\Delta)^\frac12H(\xi)\right)\right.\\ & \quad+\left.\lambda^2\log\frac1\lambda\Phi_3(\xi)+\lambda^2\Phi_4(\xi)\dots+\lambda^m\log\frac1\lambda\Phi_{2m-1}(\xi)+\lambda^m\Phi_{2m}(\xi)\right)\\ & \quad \times (1+o(1)); \end{align*}

If $n\ge 3$,

\begin{align*} \Gamma(x_0,\lambda)& =\psi(\xi)-\left(\vphantom{\frac1\lambda}a_{n,0,1}(1+\xi_n)\lambda\partial_\nu K(\xi)+\lambda^2\Phi_2(\xi)+\dots+\lambda^{n-2}\Phi_{n-2}(\xi)\right.\\ & \quad+\left.\lambda^{n-1}\log\frac1\lambda\Phi_{n-1}(\xi)+\lambda^{n-1}\Phi_n(\xi)\dots\right.\\ & \quad+\left.\lambda^m\log\frac1\lambda\Phi_{2m-n+1}(\xi)+\lambda^m\Phi_{2m-n+2}(\xi)\right)(1+o(1)). \end{align*}

Here $\mathtt a({\mathfrak {D}}_n),\,\mathtt b({\mathfrak {D}}_n),\,a_{n,0,1},\,\Phi _j(\xi )$ are given in definition 2.1.

4. The linear theory

In this section, we develop the technicalities of the Ljapunov–Schmidt finite dimensional reduction. Most of the results hereby presented are well-known in the literature of this argument, therefore details of the proofs will be skipped.

4.1. The $2$-dimensional case

It is known (see [Reference Jevnikar, López-Soriano, Medina and Ruiz34]) that the solutions of the linear problem

\begin{align*} \left\{\begin{array}{@{}ll} -\Delta\psi+2e^{U_{x_0,\lambda}}\psi=0 & \hbox{in }{\mathbb{B}^2}\\ \partial_\nu\psi-{\mathfrak{D}} e^{\frac{U_{x_0,\lambda}}2}\psi=0 & \hbox{on }{\mathbb{S}}^1\\ \end{array}\right. \end{align*}

are a linear combination of

\begin{align*} \mathcal{Z}^1_{x_0,\lambda}(z):=\partial_{x_0}U_{x_0,\lambda}\quad\hbox{and}\quad\mathcal{Z}^2_{x_0,\lambda}(z):=\partial_\lambda U_{x_0,\lambda}\quad\hbox{and} \end{align*}

given $\kappa >0$, set

(4.1)\begin{equation} \mathtt C_\kappa:=\left\{(t,x_0,\lambda)\in\mathbb{R}\times(0,\infty)\times\mathbb{R}^{n-1}\ : \frac1\kappa\le|t|+\lambda\le\kappa,\ |x_0|\le\kappa\right\}. \end{equation}

Arguing as in theorem 3.3 of [Reference Battaglia, Medina and Pistoia6] we can prove that

Proposition 4.1 Fix $p>1$ and $\kappa >0$. For any $(x_0,\,\lambda )\in \mathtt C_\kappa$ (see (4.1)) and $\mathfrak f\in L^p\left ({\mathbb {B}^2}\right )$ and $\mathfrak g\in L^p\left ({\mathbb {S}}^1\right )$ such that

\begin{align*} \int_{\mathbb{B}^2}\mathfrak f+\int_{{\mathbb{S}}^1}\mathfrak g=\int_{\mathbb{B}^2}\mathfrak f\mathcal{Z}_{x_0,\lambda}^i+\int_{{\mathbb{S}}^1}\mathfrak g\mathcal{Z}_{x_0,\lambda}^i=0,\quad i=1,2, \end{align*}

there exists a unique $\phi \in H^1\left ({\mathbb {B}^2}\right )$ such that

(4.2)\begin{align} & -2\int_{\mathbb{B}^2} e^{U_{x_0,\lambda}}\phi+{\mathfrak{D}}\int_{{\mathbb{S}}^1}e^\frac{U_{x_0,\lambda}}2\phi\nonumber\\ & \quad ={-}2\int_{\mathbb{B}^2} e^{U_{x_0,\lambda}}\phi\mathcal{Z}_{x_0,\lambda}^i+{\mathfrak{D}}\int_{{\mathbb{S}}^1}e^\frac{U_{x_0,\lambda}}2\phi\mathcal{Z}_{x_0,\lambda}^i=0,\quad i=1,2, \end{align}

which solves the problem

\begin{align*} \begin{cases}-\Delta\phi+2e^{U_{x_0,\lambda}}\phi=\mathfrak f & \hbox{in }{\mathbb{B}^2}\\ \partial_\nu\phi-{\mathfrak{D}} e^\frac{U_{x_0,\lambda}}2\phi=\mathfrak g & \hbox{on }{\mathbb{S}}^1\\ \end{cases} \end{align*}

Furthermore

\begin{align*} \|\phi\|\lesssim\left(\|\mathfrak f\|_{L^p\left({\mathbb{B}^2}\right)}+\|\mathfrak g\|_{L^p\left({\mathbb{S}}^1\right)}\right). \end{align*}

4.1.1. Rewriting the problem

We look for a solution of ($P^2_\varepsilon$) in the form

\begin{align*} u=U_{ x_0,\lambda}+\tau+\phi,\ \hbox{with}\ \lambda>0,\ x_0\in\mathbb{R}\quad\hbox{and}\quad\tau=t\sqrt\varepsilon,\ t\in\mathbb{R} \end{align*}

where $\phi$ satisfies the orthogonality condition (4.2). We shall rewrite problem ($P^2_\varepsilon$) as a system

(4.3)\begin{equation} \left\{\begin{array}{@{}ll}-\Delta\phi+2e^{U_{x_0,\lambda}}\phi=\mathscr E_{in}+\mathscr N_{in}(\phi)+c_0+\sum\limits_{i=1,2}c_i\mathcal{Z}_{x_0,\lambda}^i & \hbox{in }{\mathbb{B}^2}\\ \partial_\nu\phi-{\mathfrak{D}} e^{\frac{U_{x_0,\lambda}}2}\phi=\mathscr E_{bd}+\mathscr N_{bd}(\phi)+c_0+\sum\limits_{i=1,2}c_i\mathcal{Z}_{x_0,\lambda}^i & \hbox{on }{\mathbb{S}}^1\end{array}\right. \end{equation}

where $c_i$'s are real numbers.

The error that we are paying by using this approximating solution equals to

\begin{align*} \mathscr E_{in}:={-}\varepsilon\mathcal{F}\left(U_{x_0,\lambda}+\tau\right)\quad\hbox{and}\quad\mathscr E_{bd}:=\varepsilon\mathcal{G}\left(U_{x_0,\lambda}+\tau\right) \end{align*}

and the non-linear part is

(4.4)\begin{align} \mathscr N_{in}(\phi)& :={-}\left[\mathcal{F}\left(U_{x_0,\lambda}+\tau+\phi\right)- \mathcal{F}\left(U_{x_0,\lambda}+\tau\right)-\mathcal{F}'\left(U_{x_0,\lambda}\right)\phi\right]\nonumber\\ & \quad - \left[\left(\mathcal{F}'\left(U_{x_0,\lambda}+\tau\right)-\mathcal{F}'\left(U_{x_0,\lambda}\right)\right)\phi\right]\nonumber\\ & \quad-\varepsilon K\left[\mathcal{F}\left(U_{x_0,\lambda}+\tau+\phi\right)- \mathcal{F}\left(U_{x_0,\lambda}+\tau\right)\right];\nonumber\\ \mathscr N_{bd}(\phi)& :={-}\left[\mathcal{G}\left(U_{x_0,\lambda}+\tau+\phi\right)- \mathcal{G}\left(U_{x_0,\lambda}\right)-\mathcal{G}'\left(U_{x_0,\lambda}\right)\phi\right]\nonumber\\ & \quad -\left[\left(\mathcal{G}'\left(U_{x_0,\lambda}+\tau\right)- \mathcal{G}'\left(U_{x_0,\lambda}\right)\right)\phi\right]\nonumber\\ & \quad-\varepsilon H\left[\mathcal{G}\left(U_{x_0,\lambda}+\phi\right)- \mathcal{G}\left(U_{x_0,\lambda}\right)\right]). \end{align}

Here we set

\begin{align*} \mathcal{F}(u):=2e^u\quad\hbox{and}\quad\mathcal{G}(u)=2{\mathfrak{D}} e^\frac u2. \end{align*}

We have the following result

Proposition 4.2 Fix $\kappa >0$. There exists $\varepsilon _\kappa >0$ such that or any $(x_0,\,\lambda )\in \mathtt C_\kappa$ (see (4.1)) there exists a unique $\phi =\phi (\varepsilon,\,x_0,\,\lambda )\in H^1\left ({\mathbb {B}^2}\right )$ and $c_i\in \mathbb {R}$ which solve (4.3). Moreover, $(x_0,\,\lambda )\to \phi (\varepsilon,\,x_0,\,\lambda )$ is a $C^1-$function and $\|\phi \|\lesssim \varepsilon.$

Proof. The proof is standard and relies on a contraction mapping argument combined with the linear theory developed in proposition 4.1 and the estimates for $p>1$

\begin{align*} \|\mathscr E_{in}\|_{L^p\left({\mathbb{B}^2}\right)}\lesssim\varepsilon\quad\hbox{and}\quad\|\mathscr E_{bd}\|_{L^p\left({\mathbb{S}}^1\right)}\lesssim\varepsilon. \end{align*}

4.1.2. The reduced energy

Let us consider the energy functional $J_\varepsilon ^2$ defined in (3.1), whose critical points produce solutions of ($P^2_\varepsilon$). We define the reduced energy

\begin{align*} \widetilde J^2_\varepsilon(t,x_0,\lambda):=J^2_\varepsilon\left(U_{x_0,\lambda}+t+\phi\right), \end{align*}

where $\phi$ is given in proposition 4.2.

Proposition 4.3 The following are true:

(1) If $(x_0,\,\lambda )$ is a critical point of $\widetilde J_\varepsilon$, then $U_{x_0,\lambda }+\phi$ is a solution to ($P^2_\varepsilon$).
(2) The following expansion holds
\begin{align*} \widetilde J_\varepsilon(t,x_0,\lambda)=\mathtt E_{2,{\mathfrak{D}}}-\varepsilon\left(\alpha_{\mathfrak{D}} t^2+\Gamma(x_0,\lambda)\right)+o(\varepsilon) \end{align*}
$C^1$-uniformly in compact sets of $\mathbb {R}\times (0,\,+\infty )\times \mathbb {R}$.
Here $\mathtt E_{2,{\mathfrak {D}}}$ is a constant independent on $x_0$, $t$ and $\lambda$ whose expression is given by (3.3), $\Gamma$ is defined in (3.5) and
\begin{align*} \alpha_{\mathfrak{D}}=\pi\left(\frac{\mathfrak{D}}{\sqrt{{\mathfrak{D}}^2-1}}-2\right). \end{align*}

Proof. We use the choice $\tau =t\sqrt \varepsilon$ and the fact that

\begin{align*} {\mathfrak{D}}\int_{{\mathbb{S}}^1}e^\frac{U_{x_0,\lambda}}2{\rm d}\sigma-\int_{\mathbb{B}^2} e^{U_{x_0,\lambda}}{\rm d}x=2\pi\quad\hbox{and}\quad \int_{{\mathbb{S}}^1}e^\frac{U_{x_0,\lambda}}2{\rm d}\sigma=2\pi. \end{align*}

4.2. The $n$-dimensional case

Recently, in [Reference Cruz-Blázquez, Pistoia and Vaira21], it has been proved that all the solutions to the linearized problem

\begin{align*} \left\{\begin{array}{@{}ll} -\dfrac{4(n-1)}{n-2}\Delta Z={-}\dfrac{n+2}{n-2}{U_{x_0,\lambda}}^{\frac4{n-2}}Z & \hbox{in }\mathbb{B}^n,\\ \dfrac2{n-2}\partial_\nu Z+Z=\dfrac n{(n-2)\sqrt{n(n-1)}}{\mathfrak{D}}{ U_{x_0,\lambda}}^{\frac2{n-2}}Z & \hbox{on }{\mathbb{S}^{n-1}}\end{array}\right. \end{align*}

are a linear combination of the $n$ functions

\begin{align*} Z^i_{x_0,\lambda}=\partial_{x_{0,i}}U_{x_0,\lambda},\ i=1,\dots,n-1\quad\hbox{and}\quad Z^n_{x_0,\lambda}=\partial_\lambda U_{x_0,\lambda}. \end{align*}

Given $\kappa >0$ set

(4.5)\begin{equation} \mathtt C_\kappa:=\left\{( x_0,\lambda)\in(0,\infty)\times\mathbb{R}^{n-1}\ :\ \frac1\kappa\le\lambda\le\kappa,\ |x_0|\le\kappa\right\}. \end{equation}

Arguing as in [Reference Cruz-Blázquez, Pistoia and Vaira21] we can prove that

Proposition 4.4 Fix $\kappa >0$. For any $(x_0,\,\lambda )\in \mathtt C_\kappa$ (see (4.5)) and $\mathfrak f\in L^\frac {2n}{n+2}\left (\mathbb {B}^n\right )$ and $\mathfrak g\in L^\frac {2(n-1)}n\left ({\mathbb {S}^{n-1}}\right )$ such that

\begin{align*} \int_{\mathbb{B}^n}\mathfrak f\mathcal{Z}_{x_0,\lambda}^i+\int_{{\mathbb{S}^{n-1}}}\mathfrak g\mathcal{Z}_{x_0,\lambda}^i=0,\quad i=1,\ldots,n, \end{align*}

there exists a unique $\phi \in H^1\left (\mathbb {B}^n\right )$ such that

(4.6)\begin{align} & -\frac{n+2}{n-2}\int_{\mathbb{B}^n}{U_{x_0,\lambda}}^\frac4{n-2}\phi\mathcal{Z}_{x_0,\lambda}^i\nonumber\\& \quad +\frac n{(n-2)\sqrt{n(n-1)}}{\mathfrak{D}}\int_{{\mathbb{S}^{n-1}}}{U_{x_0,\lambda}}^\frac2{n-2}\phi\mathcal{Z}_{x_0,\lambda}^i=0,\quad i=1,\dots,n, \end{align}

which solves the problem

\begin{align*} \begin{cases} \displaystyle-\Delta\phi+\frac{n+2}{4(n-1)}{U_{x_0,\lambda}}^\frac4{n-2}\phi=\mathfrak f & \hbox{in }\;\mathbb{B}^n\\ \displaystyle\partial_\nu\phi+\frac{n-2}2\phi-\frac n{2\sqrt{n(n-1)}}{\mathfrak{D}}{U_{x_0,\lambda}}^\frac2{n-2}\phi=\mathfrak g & \hbox{on }\;{\mathbb{S}^{n-1}}\\ \end{cases} \end{align*}

Furthermore

\begin{align*} \|\phi\|\lesssim\left(\|\mathfrak f\|_{L^\frac{2n}{n+2}\left(\mathbb{B}^n\right)}+\|\mathfrak g\|_{L^\frac{2(n-1)}n\left({\mathbb{S}^{n-1}}\right)}\right). \end{align*}

4.2.1. Rewriting the problem

We look for a positive solution of ($P^n_\varepsilon$) as

\begin{align*} u=U_{ x_0,\lambda}+\phi\ \hbox{with}\ \lambda>0,\ x_0\in\mathbb{R} \end{align*}

where $\phi$ satisfies (4.6). We rewrite problem ($P^n_\varepsilon$) as a system

(4.7)\begin{equation} \left\{\begin{array}{@{}ll} -\Delta\phi+\dfrac{n+2}{4(n-1)}{U_{x_0,\lambda}}^{\frac4{n-2}}\phi=\mathscr E_{in}+\mathscr N_{in}(\phi)+\sum\limits_{i=1}^nc_i\mathcal{Z}_{x_0,\lambda}^i & \hbox{in } Bd\\ \partial_\nu\phi\,{+}\,\dfrac{n-2}2\phi-\dfrac n{2\sqrt{n(n-1)}}{\mathfrak{D}}{U_{x_0,\lambda}}^{\frac2{n-2}}\phi=\mathscr E_{bd}\,{+}\,\mathscr N_{bd}(\phi)\,{+}\,\sum\limits_{i=1}^nc_i\mathcal{Z}_{x_0,\lambda}^i & \hbox{in } Sph^1\\ \end{array}\right. \end{equation}

where the $c_i$ are real numbers. Moreover, the error is given by

\begin{align*} \mathscr E_{in}:={-}\varepsilon\mathcal{F}\left(U_{x_0,\lambda}\right)\quad\hbox{and}\quad\mathscr E_{bd}:=\varepsilon\mathcal{G}\left(U_{x_0,\lambda}\right) \end{align*}

and the non-linear part is

(4.8)\begin{align} \mathscr N_{in}(\phi)& :={-}\left[\mathcal{F}\left(U_{x_0,\lambda}+\phi\right)- \mathcal{F}\left(U_{x_0,\lambda}\right)-\mathcal{F}'\left(U_{x_0,\lambda}\right)\phi\right]\nonumber\\& \quad -\varepsilon K\left[\mathcal{F}\left(U_{x_0,\lambda}+\phi\right)- \mathcal{F}\left(U_{x_0,\lambda}\right)\right]\nonumber\\ \mathscr N_{bd}(\phi)& :={-}\left[\mathcal{G}\left(U_{x_0,\lambda}+\phi\right)- \mathcal{G}\left(U_{x_0,\lambda}\right)-\mathcal{G}'\left(U_{x_0,\lambda}\right)\phi\right]\nonumber\\& \quad -\varepsilon H\left[\mathcal{G}\left(U_{x_0,\lambda}+\phi\right)- \mathcal{G}\left(U_{x_0,\lambda}\right)\right]) \end{align}

Here we set

\begin{align*} \mathcal{F}(u):={-}\frac{n-2}{4(n-1)}(u^+)^{\frac{n+2}{n-2}}\quad\hbox{and}\quad\mathcal{G}(u)=\frac{n-2}{2\sqrt{n(n-1)}}{\mathfrak{D}}(u^+)^{\frac n{n-2}}. \end{align*}

We have the following result:

Proposition 4.5 Fix $\kappa >0$. There exists $\varepsilon _\kappa >0$ such that or any $(x_0,\,\lambda )\in \mathtt C_\kappa$ (see (4.5)) there exists a unique $\phi =\phi (\varepsilon,\,x_0,\,\lambda )\in H^1\left ({\mathbb {B}^2}\right )$ and $c_i\in \mathbb {R}$ which solve (4.7). Moreover, $(x_0,\,\lambda )\to \phi (\varepsilon,\,x_0,\,\lambda )$ is a $C^1-$function and $\|\phi \|\lesssim \varepsilon.$

Proof. The proof is standard and relies on a contraction mapping argument combined with the linear theory developed in proposition 4.4 and the estimates

\begin{align*} \|\mathscr E_{in}\|_{L^\frac{2n}{n+2}\left({\mathbb{B}^2}\right)}\lesssim\varepsilon\quad\hbox{and}\quad\|\mathscr E_{bd}\|_{L^\frac{2(n-1)}n\left({\mathbb{S}}^1\right)}\lesssim\varepsilon. \end{align*}

4.2.2. The reduced energy

We consider the functional $J^n_\varepsilon$ defined on (3.2). It is easy to see that its critical points are positive solutions to equation ($P^n_\varepsilon$). Now, we introduce the reduced energy

\begin{align*} \widetilde J^n_\varepsilon(x_0,\lambda):=J^n_\varepsilon\left(U_{x_0,\lambda}+\phi\right), \end{align*}

where $\phi$ is given in proposition 4.5. It is quite standard to prove the following result

Proposition 4.6 The following assertions hold true

(1) If $(x_0,\,\lambda )$ is a critical point of $\widetilde J_\varepsilon$, then $U_{x_0,\lambda }+\phi$ is a solution to ($P^n_\varepsilon$).
(2) Moreover, we have the following expansion
\begin{align*} \widetilde J^n_\varepsilon(x_0,\lambda)=\mathtt E_{n,{\mathfrak{D}}}-\varepsilon\Gamma(x_0,\lambda)+o(\varepsilon) \end{align*}
$C^1$-uniformly with respect to $(x_0,\,\lambda )$ in compact sets of $(0,\,+\infty )\times \mathbb {R}^{n-1}.$
Here $\mathtt E_{n,{\mathfrak {D}}}$ is a constant independent on $x_0$ and $\lambda$, given by (3.4), and $\Gamma$ is the function defined on (3.5)

5. Existence of critical points of $\Gamma$

In this section, we are finally able to get critical points of the map $(x_0,\,\lambda )\mapsto \Gamma (x_0,\,\lambda )$, hence solutions to problems ($P^2_\varepsilon$), ($P^n_\varepsilon$).

We start with the following abstract result about critical points of maps defined on balls in dependence of the boundary behaviour.

Proposition 5.1 Let $f:{\mathbb {B}^n}\to \mathbb {R}$ be a $C^1$ map satisfying, as $\xi$ goes to ${\mathbb {S}^{n-1}}$,

\begin{align*} f(\xi)=f_0\left(\frac\xi{|\xi|}\right)+g_{\frac\xi{|\xi|}}(1-|\xi|)f_1\left(\frac\xi{|\xi|}\right)+o\left(g_{\frac\xi{|\xi|}}(1-|\xi|)\right), \end{align*}

for some $f_i:{\mathbb {S}^{n-1}}\to \mathbb {R}$ with $f_0$ of class $C^1$ and some increasing $g_{\frac \xi {|\xi |}}:(0,\,1)\to (0,\,+\infty )$ such that $g_{\frac \xi {|\xi |}}(t)\underset {t\to 0}\to 0$.

If one of the following holds true:

(1) $f_1(\xi )>0$ at any global maximum $\xi$ of $f_0$;
(2) $f_1(\xi )<0$ at any global minimum $\xi$ of $f_0$;
(3) $f_1(\xi )\ne 0$ at any critical point $\xi$ of $f_0$, $f_0$ is Morse and
\begin{align*} \sum_{\{\xi:\nabla f_0(\xi)=0,\,f_1(\xi)>0\}}({-}1)^{\operatorname{ind}_\xi\nabla f_0}\ne1; \end{align*}

then, $f$ has at least a stable critical point.

Theorems 1.1 and 1.2 will follow without much difficulty from this proposition and proposition 3.4.

Proof of theorems 1.1 and 1.2 We only consider the case of theorem 1.1, since the same arguments also work for theorem 1.2.

Thanks to proposition 4.3, we get a solutions to the problem ($P^2_\varepsilon$) whenever $\frac {\mathfrak {D}}{\sqrt {{\mathfrak {D}}^2-1}}-2\ne 0$, that is ${\mathfrak {D}}\ne \frac 2{\sqrt 3}$, and $(x_0,\,\lambda )$ is a stable critical point of $\Gamma$. After composing with $\mathscr {I}$, this is equivalent to getting a critical point of the map $f(\xi )=\Gamma \left (\mathscr {I}^{-1}(\xi )\right )$, which is well-defined and smooth in the whole $\overline {\mathbb {B}^n}$ thanks to proposition 3.3.

In view of proposition 3.4, $f$ satisfies the assumptions of proposition 5.1 with

\begin{align*} f_0& =\psi,\quad g_\xi(t)=\left\{\begin{array}{@{}ll}t & \hbox{if }\nabla\psi(\xi)\ne0\\ t^{\lfloor\frac{m+1}2\rfloor}\log^{\frac{1-({-}1)^m}2}\dfrac1\lambda & \mbox{if }\nabla\psi(\xi)=0\end{array}\right.,\\ f_1& =\left\{\begin{array}{@{}ll}-2\pi\Phi_1 & \hbox{if }\nabla\psi(\xi)\ne0\\-\Phi_m & \mbox{if }\nabla\psi(\xi)=0\end{array}\right., \end{align*}

with $m=m(\xi )$ as in theorem 1.1 (if $m(\xi )$ is not well-defined, as for minima of $\psi$ in case (1) or maxima of $\psi$ in case (2), one can just set $g_\xi (t)=t,\,f_1=-2\pi \Phi _1$).

Here, we used that $\lambda =\frac {1-|\xi |}{1+\xi _n}+o(1-|\xi |)$ and that

\begin{align*} a_{2,0,0}& =4\int_{\mathbb{R}^2_+}\frac1{\left(\bar y^2+(y_2+{\mathfrak{D}})^2-1\right)^2}{\rm d}\bar y{\rm d}y_2=\frac{2\pi}{\sqrt{{\mathfrak{D}}^2-1}}\left({\mathfrak{D}}-\sqrt{{\mathfrak{D}}^2-1}\right)\\ b_{2,0}& =4\frac{\mathfrak{D}}{\sqrt{{\mathfrak{D}}^2-1}}\int_{\partial\mathbb{R}^2_+}\frac1{\bar y^2+1}{\rm d}\bar y=\frac{4\pi{\mathfrak{D}}}{\sqrt{{\mathfrak{D}}^2-1}} \end{align*}

hence the two definitions of $\psi$ given in theorem 1.1 and proposition 3.4 actually coincide.

Since $-2\pi <0$, then the assumptions on $K,\,H$ in theorem 4.3 are equivalent to the ones in proposition 5.1, hence they ensure existence of solutions.

To prove proposition 5.1, we will compute the Leray–Schauder degree of the map $f$.

Proof of proposition 5.1 First of all, $f$ can be extended up to ${\mathbb {S}^{n-1}}$ as $f_0$. Since $g$ vanishes at $0$, this extension is continuous.

Assume $(1)$ holds and take an absolute maximum point $\xi _0$ for $f$ on $\overline {\mathbb {B}^n}$. To get a critical point for $f$ on ${\mathbb {B}^n}$ we suffice to show that $\xi _0\not \in {\mathbb {S}^{n-1}}$.

If $\xi _0\in {\mathbb {S}^{n-1}}$, we would have $f_1(\xi _0)>0$, therefore, for $0< t\ll 1$ we would have

\begin{align*} f((1-t)\xi_0)=f_0(\xi_0)+g_{\xi_0}(t)f_1(\xi_0)+o(g_{\xi_0}(t))>f_0(\xi_0), \end{align*}

contradicting the fact that $\xi _0$ is a maximum point.

If $(2)$ holds, then the same argument shows that the minimum of $f$ on $\overline {\mathbb {B}^n}$ lies in the interior of ${\mathbb {B}^n}$, therefore it is a critical point of $f$.

Assume now that $(3)$ holds. We consider the double of $\overline {\mathbb {B}^n}$, namely the manifold obtained by gluing two copies of ${\mathbb {B}^n}$ along the boundary: $\frac {\overline {\mathbb {B}^n}\times \{0,\,1\}}\sim$, where $(\xi,\,0)\sim (\xi,\,1)$ for $\xi \in {\mathbb {S}^{n-1}}$. This manifold is clearly diffeomorphic to $\mathbb {S}^n$, hence we will identify it as $\mathbb {S}^n$.

$f$ can be naturally extended to $\tilde f:\mathbb {S}^n\to \mathbb {R}$ as $\tilde f(\xi,\,i)=f(\xi )$ for $i=0,\,1$. The extension is continuous and, after a suitable rescalement of $g$ close to $0$, of class $C^1$ (with vanishing normal derivative on the equator). Such a rescalement does not affect the presence of critical points to $\tilde f$, $f$ and $f|_{{\mathbb {S}^{n-1}}}=f_0$, which we will now investigate.

We use the Euler–Poincaré formula to compute the Leray–Schauder degree of $\tilde f$, which is a Morse function by assumption:

\begin{align*} 1+({-}1)^n=\chi\left(\mathbb{S}^n\right)& =\sum_{\{\xi\in{\mathbb{S}^{n-1}}:\nabla\tilde f(\xi)=0\}}({-}1)^{\operatorname{ind}_\xi\nabla\tilde f}+\sum_{\{\xi\not\in{\mathbb{S}^{n-1}}:\nabla\tilde f(\xi)=0\}}({-}1)^{\operatorname{ind}_\xi\nabla\tilde f}\\ & =\sum_{\{\xi\in{\mathbb{S}^{n-1}}:\nabla\tilde f(\xi)=0\}}({-}1)^{\operatorname{ind}_\xi\nabla\tilde f}+2\sum_{\{\xi\in{\mathbb{B}^n}:\nabla f(\xi)=0\}}({-}1)^{\operatorname{ind}_\xi\nabla f}. \end{align*}

To deal with the critical points on ${\mathbb {S}^{n-1}}$, we notice that they are exactly the same critical points of $f_0$, but their index may change, since each can be either a minimum or a maximum in the orthogonal direction; precisely:

\begin{align*} f_1(\xi)>0& \Rightarrow\operatorname{ind}_\xi\nabla\tilde f=\operatorname{ind}_\xi\nabla f_0;\\ f_1(\xi)<0& \Rightarrow\operatorname{ind}_\xi\nabla\tilde f=\operatorname{ind}_\xi\nabla f_0+1 \end{align*}

and so

\begin{align*} & \sum_{\{\xi\in{\mathbb{S}^{n-1}}:\nabla\tilde f(\xi)=0\}}({-}1)^{\operatorname{ind}_\xi\nabla\tilde f}\\& \quad =\sum_{\{\xi:\nabla f_0(\xi)=0,\,f_1(\xi)>0\}}({-}1)^{\operatorname{ind}_\xi\nabla f_0}-\sum_{\{\xi:\nabla f_0(\xi)=0,\,f_1(\xi)<0\}}({-}1)^{\operatorname{ind}_\xi\nabla f_0}. \end{align*}

Therefore, applying again the Euler–Poincaré formula, this time to $f_0$ on ${\mathbb {S}^{n-1}}$, we get:

\begin{align*} 1-({-}1)^n& =\chi\left({\mathbb{S}^{n-1}}\right)\\ & =\sum_{\{\xi\in{\mathbb{S}^{n-1}}:\nabla f_0(\xi)=0\}}({-}1)^{\operatorname{ind}_\xi\nabla f_0}\\ & =\sum_{\{\xi:\nabla f_0(\xi)=0,\,f_1(\xi)>0\}}({-}1)^{\operatorname{ind}_\xi\nabla f_0}+\sum_{\{\xi:\nabla f_0(\xi)=0,\,f_1(\xi)<0\}}({-}1)^{\operatorname{ind}_\xi\nabla f_0}. \end{align*}

By summing the previous equalities we get:

\begin{align*} \sum_{\{\xi\in{\mathbb{B}^n}:\nabla f(\xi)=0\}}({-}1)^{\operatorname{ind}_\xi\nabla f}=1-\sum_{\{\xi\in{\mathbb{S}^{n-1}}:\nabla f_0(\xi)=0,\,f_1(\xi)>0\}}({-}1)^{\operatorname{ind}_\xi\nabla f_0}. \end{align*}

The latter quantity is non-zero by assumptions, therefore the set of critical points of $f$ on ${\mathbb {B}^n}$, on which we are taking the first sum, cannot be empty.

Acknowledgements

S. C. acknowledges financial support from the Spanish Ministry of Universities and Next Generation EU funds, through a Margarita Salas grant from the University of Granada, by the FEDER-MINECO Grant PID2021-122122NB-I00 and by J. Andalucia (FQM-116). This work was carried out during his long visit to the University ‘Sapienza Universitá di Roma’, to which he is grateful. The three authors are partially supported by the group GNAMPA of the Istituto Nazionale di Alta Matematica (INdAM). In particular, the first and second authors are funded by the project ‘Fenomeni di blow-up per equazioni nonlineari’, project code CUP_E55F22000270001.

Appendix A. Proof of proposition 3.4

By introducing a rotation in ${\mathbb {B}^n}$ and moving to $\mathbb {R}^n_+$ via $\mathscr {I}$ we can give an expression for $\Gamma$ which is more convenient for our computation.

Lemma A.1 Let $A:{\mathbb {B}^n}\to {\mathbb {B}^n}$ be the rotation corresponding, via the $\mathscr {I}$, to the translation of $T:x\to x+x_0$ on the half-place, namely $A=\mathscr {I}\circ T\circ \mathscr {I}^{-1}$. There holds:

\begin{align*} \Gamma(x_0,\lambda)& =\Lambda_n^\frac n2\int_{\mathbb{R}^n_+}\frac{\tilde K_A(\lambda y)}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y {\rm d}y_n\nonumber\\& \quad -\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}}\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\lambda\bar y)}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y, \end{align*}

where $\tilde K_A=K\circ A\circ \mathscr {I},\,\tilde H_A=H\circ A\circ \mathscr {I}$.

Proof. By doing a change of variables, we observe that

\begin{align*} \Gamma(x_0,\lambda)& =\int_{\mathbb{B}^n} K_A(z)P_{x_0,\lambda}(Az)^\frac n2-\beta_n{\mathfrak{D}}\int_{\mathbb{S}^{n-1}} H_A(z)P_{x_0,\lambda}(Az)^\frac{n-1}2\\ & =\int_{\mathbb{B}^n} K_A(z)P_{0,\lambda}(z)^\frac n2-\beta_n{\mathfrak{D}}\int_{\mathbb{S}^{n-1}} H_A(z)P_{0,\lambda}(z)^\frac{n-1}2. \end{align*}

Here we are using that $A$ is a rotation and its very definition, and we set $K_A\!=\!K\circ A, H_A=H\circ A$. Finally, changing variables twice and using the definitions in § 2:

\begin{align*} \Gamma(x_0,\lambda)& =\Lambda_n^\frac n2\int_{\mathbb{R}^n_+}\frac{\tilde K_A(x)\lambda^n}{\left(\left\vert \bar x\right\vert^2+(x_n+\lambda{\mathfrak{D}})^2-\lambda^2\right)^n}{\rm d}\bar x{\rm d}x_n\\& \quad +\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}}\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\bar x)\lambda^{n-1}}{\left(\left\vert \bar x\right\vert^2+\lambda^2\left({\mathfrak{D}}^2-1\right)\right)^{n-1}}{\rm d}\bar x\\ & =\Lambda_n^\frac n2\int_{\mathbb{R}^n_+}\frac{\tilde K_A(\lambda y)}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y {\rm d}y_n\\& \quad +\Lambda_n^\frac{n-1}2\beta_n{\mathfrak{D}}\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\lambda\bar y)}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y \end{align*}

Proof of proposition 3.4 We start by estimating the boundary term, where some cancellations occur due to symmetry. We expand $\tilde H_A(\lambda y)$ in $\lambda$ up to order $n-2$:

\begin{align*} & \int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\lambda\bar y)}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y\\ & \quad=\tilde H_A(0)\int_{\partial\mathbb{R}^n_+}\frac{{\rm d}\bar y}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}\\ & \qquad+\sum_{1\le|\alpha|\le n-2}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\int_{\partial\mathbb{R}^n_+}\frac{\bar y^\alpha}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y\\ & \qquad+\underbrace{\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\lambda\bar y)-\sum_{|\alpha|\le n-2}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar y^\alpha}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y}_{=:I}\\ & \quad=H(\xi)\int_{\partial\mathbb{R}^n_+}\frac{{\rm d}\bar y}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}\\ & \qquad+\lambda^2\frac1{4(n-1)}\Delta\tilde H_A(0)\int_{\partial\mathbb{R}^n_+}\frac{|\bar y|^2}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y+\dots \\ & \qquad+\lambda^{2\lfloor\frac{n-2}2\rfloor}\frac{(n-3)!!}{\left(2\lfloor\frac{n-2}2\rfloor\right)!\left(2\lfloor\frac{n-2}2\rfloor\right)!!\left(n-3+2\lfloor\frac{n-2}2\rfloor\right)!!}\Delta^{\lfloor\frac{n-2}2\rfloor}\tilde H_A(0)\\ & \qquad\times\int_{\partial\mathbb{R}^n_+}\frac{|\bar y|^{2\lfloor\frac{n-2}2\rfloor}}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y+I\\ & \quad=\frac{H(\xi)}{\left({\mathfrak{D}}^2-1\right)^\frac{n-1}2}\int_{\partial\mathbb{R}^n_+}\frac{{\rm d}\bar y}{\left(\left\vert \bar y\right\vert^2+1\right)^{n-1}}\\ & \qquad+\lambda^2\frac1{\left({\mathfrak{D}}^2-1\right)^\frac{n-3}2}\frac1{4(n-1)}\Delta\tilde H_A(0)\int_{\partial\mathbb{R}^n_+}\frac{|\bar y|^2}{\left(\left\vert \bar y\right\vert^2+1\right)^{n-1}}{\rm d}\bar y+\dots\\ & \qquad+\lambda^{2\lfloor\frac{n-2}2\rfloor}\frac1{\left({\mathfrak{D}}^2-1\right)^\frac{n-2\lfloor\frac{n-2}2\rfloor}2-1}\frac{(n-3)!!}{\left(2\lfloor\frac{n-2}2\rfloor\right)!\left(2\lfloor\frac{n-2}2\rfloor\right)!!\left(n-3+2\lfloor\frac{n-2}2\rfloor\right)!!}\\ & \qquad\times\Delta^{\lfloor\frac{n-2}2\rfloor}\tilde H_A(0)\int_{\partial\mathbb{R}^n_+}\frac{|\bar y|^{2\lfloor\frac{n-2}2\rfloor}}{\left(\left\vert \bar y\right\vert^2+1\right)^{n-1}}{\rm d}\bar y\\ & \qquad+ I, \end{align*}

where we used the formula

(A.1)\begin{equation} \Delta^j|y|^{2j}=\frac{(2j)!!(n-3+2j)!!}{(n-3)!!} \end{equation}

and the vanishing, due to symmetry, of integrals of homogeneous polynomials of odd degree or of degree $2j$ which are $j$-harmonic.

Moreover, in view of the conformal properties of the Laplacian, one has

(A.2)\begin{equation} \Delta^j\tilde H_A(0)=(1+\xi_n)^{2j}\Delta^jH(\xi), \end{equation}

hence the $j^\mathrm {th}$ term in the expansion equals

\begin{align*} \lambda^{2j}\frac1{\left({\mathfrak{D}}^2\,{-}\,1\right)^\frac{n-2j-1}2}\frac{(n-3)!!}{(2j)!(2j)!!(n\,{+}\,2j\,{-}\,3)!!}(1\,{+}\,\xi_n)^{2j}\Delta^jH(\xi)\int_{\partial\mathbb{R}^n_+}\frac{|\bar y|^{2j}}{\left(\left\vert \bar y\right\vert^2\,{+}\,1\right)^{n-1}}{\rm d}\bar y. \end{align*}

In the $j^\mathrm {th}$ order expansion, the remainder is actually $o\left (\lambda ^j\right )$ because we get

\begin{align*} & \int_{|\bar y|\le\frac1\lambda}\frac{\tilde H_A(\lambda\bar y)-\sum_{|\alpha|\le j}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar y^\alpha}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y\\& \qquad +\int_{|\bar y|>\frac1\lambda}\frac{\tilde H_A(\lambda\bar y)-\sum_{|\alpha|\le j}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar y^\alpha}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y \\ & \quad=\int_{|\bar y|\le\frac1\lambda}\frac{O\left(|\lambda\bar y|^{j+1}\right)}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y+\int_{|\bar y|>\frac1\lambda}\frac{O\left(|\lambda\bar y|^j\right)}{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}{\rm d}\bar y\\ & \quad=O\left(\lambda^{j+1}\log\frac1\lambda\right)+O\left(\lambda^{n-1}\right). \end{align*}

In order to deal with higher order terms, we need another argument, since this would get non-converging integrals.

We split the cases $n$ even and $n$ odd.

If $n$ is even, the main order term in the denominator of $I$ is of odd order, hence its integral vanishes. Therefore,

\begin{align*} I& =\lambda^{n-1}\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\bar x)-\sum_{|\alpha|\le n-2}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha}{\left(\left\vert \bar x\right\vert^2+\lambda^2\left({\mathfrak{D}}^2-1\right)\right)^{n-1}}{\rm d}\bar x\\ & =\lambda^{n-1}\int_{\partial\mathbb{R}^n_+}\frac{\begin{array}{l}\tilde H_A(\bar x)-\sum_{|\alpha|\le n-2}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha\\ \quad -\frac1{(n-1)!}\sum_{|\alpha|=n-1}\partial_{\bar x^\alpha}\tilde H_A(0)\bar x^\alpha\chi_{|x|\le1}\end{array}}{\left(\left\vert \bar x\right\vert^2+\lambda^2\left({\mathfrak{D}}^2-1\right)\right)^{n-1}}{\rm d}\bar x\\ & =\lambda^{n-1}\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\bar x)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha\chi_{|x|\le1}}{\left\vert \bar x\right\vert^{2(n-1)}}{\rm d}\bar x\\ & \quad+\int_{\partial\mathbb{R}^n_+}\left(\tilde H_A(\bar x)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha\right)\\& \quad \times \left(\frac{\lambda^{n-1}}{\left(\left\vert \bar x\right\vert^2+\lambda^2\left({\mathfrak{D}}^2-1\right)\right)^{n-1}}-\frac{\lambda^{n-1}}{|\bar x|^{2(n-1)}}\right){\rm d}\bar x\\ & \quad+O\left(\sum_{j=0}^\frac{n-2}2\Delta^j\tilde H_A(0)\lambda^{n-1}\right)\\ & =\lambda^{n-1}\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\bar x)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha\chi_{|x|\le1}}{\left\vert \bar x\right\vert^{2(n-1)}}{\rm d}\bar x\\ & \quad+\frac{\lambda^n}{n!}\sum_{|\alpha|=n}\partial_{\bar x^\alpha}\tilde H_A(0)\int_{\partial\mathbb{R}^n_+}\bar y^\alpha\left(\frac1{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}-\frac1{|\bar y|^{2(n-1)}}\right) \\ & \quad+\underbrace{\begin{array}{l}\displaystyle\int_{\partial\mathbb{R}^n_+}\left(\tilde H_A(\lambda\bar y)-\sum_{|\alpha|\le n}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar y^\alpha\right)\\\quad \displaystyle\times \left(\frac1{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}-\frac1{|\bar y|^{2(n-1)}}\right){\rm d}\bar y\end{array}}_{=:I'}\\ & \quad+o\left(\sum_{j=0}^\frac{n-2}2\Delta^j\tilde H_A(0)\lambda^{2j}\right)\\ & =\lambda^{n-1}\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\bar x)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha\chi_{|x|\le1}}{\left\vert \bar x\right\vert^{2(n-1)}}{\rm d}\bar x\\ & \quad+\lambda^n\left({\mathfrak{D}}^2-1\right)^\frac12\frac{(n-3)!!}{n!n!!(2n-3)!!}(\Delta)^\frac n2\tilde H_A(0)\\ & \quad\times \int_{\partial\mathbb{R}^n_+}|\bar y|^n\left(\frac1{\left(|\bar y|^2+1\right)^{n-1}}-\frac1{|\bar y|^{2(n-1)}}\right){\rm d}\bar y\\ & \quad+I'+o\left(\sum_{j=0}^\frac{n-2}2\Delta^j\tilde H_A(0)\lambda^{2j}\right), \end{align*}

where we used again (A.1); one easily verifies that, due to the behaviours at $0$ at infinity, all the integrals are converging, hence everything is well defined.

After changing variables, the main terms are now

\begin{align*} & \lambda^{n-1}(1+\xi_n)^{n-1}\int_{{\mathbb{S}^{n-1}}}\frac{H(z)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{\xi_\alpha}H(\xi)(z-\xi)^\alpha}{|z-\xi|^{2(n-1)}}{\rm d}z\\ & \quad+\lambda^n\left({\mathfrak{D}}^2-1\right)^\frac12\frac{(n-3)!!}{n!n!!(2n-3)!!}(1+\xi_n)^n(\Delta)^\frac n2H(\xi)\\ & \quad\times \int_{\partial\mathbb{R}^n_+}|\bar y|^n\left(\frac1{\left(|\bar y|^2+1\right)^{n-1}}-\frac1{|\bar y|^{2(n-1)}}\right){\rm d}\bar y\\ & \quad+I'+o\left(\sum_{j=0}^\frac{n-2}2\Delta^jH(\xi)\lambda^{2j}\right), \end{align*}

where we used the fact that $\frac 1{|\bar x|^2}=\frac {|z+\xi |^2}{|z-\xi |^2}$ and again (A.2). The small $o$ term contains some new quantities arising when the terms of order $\lambda ^{n-1}$ are transformed into each other.

The smallness of the remainder can be shown similarly as before, here and in the following.

Due to the asymptotic behaviour of both factors, $I'$ can be dealt with similarly as $I$ and one can iterate the argument. In particular, using the series expansion

\begin{align*} \frac1{\left(|\bar y|^2+{\mathfrak{D}}^2-1\right)^{n-1}}=\sum_{j=0}^\infty({-}1)^j\frac{(n+j-2)!}{j!(n-2)!}\frac{\left({\mathfrak{D}}^2-1\right)^j}{|\bar y|^{2(n+j-1)}}, \end{align*}

we get, for any even $m>n$, the following $m^\mathrm {th}$ order term:

\begin{align*} & \lambda^{m-1}({-}1)^\frac{m-n}2(1+\xi_n)^{m-1}\frac{\left(\frac{n+m}2-2\right)!}{\left(\frac{m-n}2\right)!(n-2)!}\left({\mathfrak{D}}^2-1\right)^\frac{m-n}2\\ & \quad\times \int_{{\mathbb{S}^{n-1}}}\left(H(z)-\sum_{|\alpha|\le m-1}\frac1{|\alpha|!}\partial_{\xi_\alpha}H(\xi)(z-\xi)^\alpha\right)\frac{|z+\xi|^{m-n}}{|z-\xi|^{n+m-2}}{\rm d}z\\ & \quad+\lambda^m\left({\mathfrak{D}}^2-1\right)^\frac{m-n+1}2\frac{(n-3)!!}{m!m!!(n+m-3)!!}(1+\xi_n)^m(\Delta)^\frac m2H(\xi)\\ & \quad\times \int_{\partial\mathbb{R}^n_+}|\bar y|^m\left(\frac1{\left(|\bar y|^2+1\right)^{n-1}}-\sum_{j=0}^\frac{m-n}2({-}1)^j\frac{(n+j-2)!}{j!(n-2)!}\frac1{|\bar y|^{2(n+j-1)}}\right){\rm d}\bar y\\ & \quad+\int_{\partial\mathbb{R}^n_+}\left(\tilde H_A(\lambda\bar y)-\sum_{|\alpha|\le m}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar y^\alpha\right)\\ & \quad\times \left(\frac1{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}-\sum_{j=0}^\frac{m-n}2({-}1)^j\frac{(n+j-2)!}{j!(n-2)!}\frac{\left({\mathfrak{D}}^2-1\right)^j}{|\bar y|^{2(n+j-1)}}\right){\rm d}\bar y\\ & \quad+o\left(\sum_{j=0}^\frac{m-2}2\Delta^jH(\xi)\lambda^{2j}\right). \end{align*}

In particular, we point out that if $n=2$ this is the main order term in the boundary estimates, and it equals

(A.3)\begin{equation} -\lambda\pi(1+\xi_n)(-\Delta)^\frac12H(\xi). \end{equation}

Let us now consider the case $n$ odd. Here, the first term does not vanish and it gives rise to a logarithmic term. In fact,

\begin{align*} I& =\lambda^{n-1}\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\bar x)-\sum_{|\alpha|\le n-2}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha}{\left(\left\vert \bar x\right\vert^2+\lambda^2\left({\mathfrak{D}}^2-1\right)\right)^{n-1}}{\rm d}\bar x \\ & =\frac{\lambda^{n-1}}{(n-1)!}\sum_{|\alpha|=n-1}\partial_{\bar x^\alpha}\tilde H_A(0)\int_{|\bar x|\le1}\frac{\bar x^\alpha}{\left(\left\vert \bar x\right\vert^2+\lambda^2\left({\mathfrak{D}}^2-1\right)\right)^{n-1}}{\rm d}\bar x\\ & \quad+\lambda^{n-1}\int_{\partial\mathbb{R}^n_+}\frac{\begin{array}{l}\tilde H_A(\bar x)-\sum_{|\alpha|\le n-2}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha\\\quad -\frac1{(n-1)!}\sum_{|\alpha|=n-1}\partial_{\bar x^\alpha}\tilde H_A(0)\bar x^\alpha\chi_{|x|\le1}\end{array}}{\left(\left\vert \bar x\right\vert^2+\lambda^2\left({\mathfrak{D}}^2-1\right)\right)^{n-1}}{\rm d}\bar x\\ & =\lambda^{n-1}\left(\log\frac1\lambda+O(1)\right)\frac{(n-3)!!}{(n-1)!(n-1)!!(2n-4)!!}\Delta^\frac{n-1}2\tilde H_A(0)\omega_{n-2}\\ & \quad+\lambda^{n-1}\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\bar x)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha\chi_{|x|\le1}}{\left(\left\vert \bar x\right\vert^2+\lambda^2\left({\mathfrak{D}}^2-1\right)\right)^{n-1}}{\rm d}\bar x\\ & \quad+O\left(\lambda^{n-1}\sum_{j=0}^\frac{n-3}2\Delta^j\tilde H_A(0)\right)\\ & =\lambda^{n-1}\log\frac1\lambda\frac{(n-3)!!}{(n-1)!(n-1)!!(2n-4)!!}\Delta^\frac{n-1}2\tilde H_A(0)\omega_{n-2}(1+o(1))\\ & \quad+\lambda^{n-1}\int_{\partial\mathbb{R}^n_+}\frac{\tilde H_A(\bar x)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha\chi_{|x|\le1}}{\left\vert \bar x\right\vert^{2(n-1)}}{\rm d}\bar x\\ & \quad-\int_{\partial\mathbb{R}^n_+}\left(\tilde H_A(\bar x)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar x^\alpha\right)\\ & \quad\times \left(\frac{\lambda^{n-1}}{|\bar x|^{2(n-1)}}-\frac{\lambda^{n-1}}{\left(\left\vert \bar x\right\vert^2+\lambda^2\left({\mathfrak{D}}^2-1\right)\right)^{n-1}}\right){\rm d}\bar x\\ & \quad+o\left(\sum_{j=0}^\frac{n-3}2\Delta^j\tilde H_A(0)\lambda^{2j}\right)\\ & =\lambda^{n-1}\log\frac1\lambda\frac{(n-3)!!}{(n-1)!(n-1)!!(2n-4)!!}(1+\xi_n)^{n-1}\Delta^\frac{n-1}2H(\xi)\omega_{n-2}(1+o(1))\\ & \quad+\lambda^{n-1}(1+\xi_n)^{n-1}\int_{{\mathbb{S}^{n-1}}}\frac{H(z)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{\xi_\alpha}H(\xi)(z-\xi)^\alpha}{|z-\xi|^{2(n-1)}}{\rm d}z\\ & \quad-\int_{\partial\mathbb{R}^n_+}\left(\tilde H_A(\lambda\bar y)-\sum_{|\alpha|\le n}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar y^\alpha\right) \\ & \quad\times \left(\frac1{|\bar y|^{2(n-1)}}-\frac1{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}\right){\rm d}\bar y\\ & \quad+o\left(\sum_{j=0}^\frac{n-3}2\Delta^j H_\xi(0)\lambda^{2j}\right); \end{align*}

iterating, for any odd $m>n$ we get

\begin{align*} & \lambda^{m-1}\log\frac1\lambda({-}1)^\frac{m-n}2\frac{(n-3)!!}{(m-1)!(m-1)!!(n+m-4)!!}\frac{\left(\frac{n+m}2-2\right)!}{\left(\frac{m-n}2\right)!(n-2)!}\left({\mathfrak{D}}^2-1\right)^\frac{m-n}2\\ & \quad\times(1+\xi_n)^{m-1}\Delta^\frac{m-1}2H(\xi)\omega_{n-2}(1+o(1))\\ & \quad+\lambda^{m-1}({-}1)^\frac{m-n}2(1+\xi_n)^{m-1}\frac{\left(\frac{n+m}2-2\right)!}{\left(\frac{m-n}2\right)!(n-2)!}\left({\mathfrak{D}}^2-1\right)^\frac{m-n}2\\ & \quad\times\int_{{\mathbb{S}^{n-1}}}\left(H(z)-\sum_{|\alpha|\le m-1}\frac1{|\alpha|!}\partial_{\xi_\alpha}H(\xi)(z-\xi)^\alpha\right)\frac{|z+\xi|^{m-n}}{|z-\xi|^{n+m-2}}{\rm d}z\\ & \quad+\int_{\partial\mathbb{R}^n_+}\left(\tilde H_A(\lambda\bar y)-\sum_{|\alpha|\le m}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{\bar x_\alpha}\tilde H_A(0)\bar y^\alpha\right)\\ & \quad\times\left(\frac1{\left(\left\vert \bar y\right\vert^2+{\mathfrak{D}}^2-1\right)^{n-1}}-\sum_{j=0}^\frac{m-n}2({-}1)^j\frac{(n+j-2)!}{j!(n-2)!}\frac{\left({\mathfrak{D}}^2-1\right)^j}{|\bar y|^{2(n+j-1)}}\right){\rm d}\bar y\\ & \quad+o\left(\sum_{j=0}^\frac{m-2}2\Delta^jH(\xi)\lambda^{2j}\right). \end{align*}

The argument to estimate the interior terms is similar. We expand $\tilde K(\lambda y)$ up to order $n-1$, which is the highest power that can be integrated against $P_{x_0,\lambda }^\frac n2$.

\begin{align*} & \int_{\mathbb{R}^n_+}\frac{\tilde K_A(\lambda y)}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y {\rm d}y_n\\ & \quad=\tilde K_A(0)\int_{\mathbb{R}^n_+}\frac{{\rm d}\bar y{\rm d}y_n}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}\\ & \qquad+ \sum_{1\le|\alpha|\le n-1}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{x_\alpha}\tilde K_A(0)\int_{\partial\mathbb{R}^n_+}\frac{y^\alpha}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y{\rm d}y_n \\ & \qquad+\underbrace{\int_{\mathbb{R}^n_+}\frac{\tilde K_A(\lambda y)-\sum_{|\alpha|\le n-1}\frac{\lambda^n}{|\alpha|}\partial_{x_\alpha}\tilde K_A(0)y^\alpha}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y {\rm d}y_n}_{=:I''}\\ & \quad=K(\xi)\int_{\mathbb{R}^n_+}\frac{{\rm d}\bar y{\rm d}y_n}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}\\ & \qquad+\lambda\partial_{x_n}\tilde K_A(\xi)\int_{\mathbb{R}^n_+}\frac{y_n}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y{\rm d}y_n\\ & \qquad+\sum_{j=2}^{n-1}\lambda^j\sum_{i=0}^{\lfloor\frac j2\rfloor}\frac1{(j-2i)!(2i)!}\frac{(n-3)!!}{(2i)!!(n+2i-3)!!}\partial_{x_n}^{j-2i}\Delta_{\bar x}^i\tilde K_A(0)\\ & \qquad\times \int_{\mathbb{R}^n_+}\frac{|\bar y|^{2i}y_n^{j-2i}}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y{\rm d}y_n +I''\\ & \quad=K(\xi)\int_{\mathbb{R}^n_+}\frac{{\rm d}\bar y{\rm d}y_n}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}\\ & \qquad-\lambda(1+\xi_n)\partial_\nu K(\xi)\int_{\mathbb{R}^n_+}\frac{y_n}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y{\rm d}y_n\\ & \qquad+\sum_{j=2}^{n-1}\lambda^j\sum_{i=0}^{\lfloor\frac j2\rfloor}\frac1{(j-2i)!(2i)!}\frac{(n-3)!!}{(2i)!!(n+2i-3)!!}({-}1)^j(1+\xi_n)^j\partial_\nu^{j-2i}\Delta_\tau^iK(\xi)\\ & \qquad\times \int_{\mathbb{R}^n_+}\frac{|\bar y|^{2i}y_n^{j-2i}}{\left(\left\vert \bar y\right\vert^2+(y_n+{\mathfrak{D}})^2-1\right)^n}{\rm d}\bar y{\rm d}y_n\\ & \qquad+I'', \end{align*}

where we wrote the derivation in $\bar x$ and $x_n$ as

\begin{align*} \sum_{|\alpha|=j}\partial_{x_\alpha}=\sum_{i=0}^j\frac{j!}{(j-i)!i!}\sum_{|\beta|=i}\partial_{x_n}^{j-i}\partial_{\bar x_\beta} \end{align*}

and used again cancellation by symmetry and (A.1). In the last step, we used (A.2) (in $\bar x$) and that

\begin{align*} \partial_{x_n}^j=({-}1)^j(1+\xi_n)^j\partial_\nu. \end{align*}

In the case $n=2$, since $\int _{\mathbb {R}^2_+}\frac {y_2}{\left (\bar y^2+(y_n+{\mathfrak {D}})^2-1\right )^n}{\rm d}\bar y{\rm d}y_2=\frac \pi 2\left (\sqrt {{\mathfrak {D}}^2-1}-{\mathfrak {D}}\right )$, putting together with (A.3) we get the first-order expansion

\begin{align*} \Gamma(x_0,\lambda)& =\psi(\xi)-2\pi(1+\xi_n)\lambda\left(\left({\mathfrak{D}}-\sqrt{{\mathfrak{D}}^2-1}\right)\,\partial_\nu K(\xi)-2{\mathfrak{D}}(-\Delta)^\frac12H(\xi)\right)\\& \quad +o(\lambda), \end{align*}

whereas when $n\ge 3$ the first-order expansion contains only the interior term:

\begin{align*} \Gamma(x_0,\lambda)=\psi(\xi)-a_{n,0,1}(1+\xi_n)\lambda\partial_\nu K(\xi). \end{align*}

As for $I''$, we get local terms involving derivatives of $\tilde K_A$ and non-local terms similarly as before:

\begin{align*} I''& =\lambda^n\int_{\mathbb{R}^n_+}\frac{\tilde K_A(x)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{x_\alpha}\tilde K_A(0)x^\alpha}{\left(\left\vert \bar x\right\vert^2+(x_n+\lambda{\mathfrak{D}})^2-\lambda^2\right)^n}{\rm d}\bar x{\rm d}x_n\\ & \quad=\frac{\lambda^n}{n!}\sum_{|\alpha|=n}\partial_{x_\alpha}\tilde K_A(0)\int_{|x|\le1}\frac{x^\alpha}{\left(\left\vert \bar x\right\vert^2+(x_n+\lambda{\mathfrak{D}})^2-\lambda^2\right)^n}{\rm d}\bar x{\rm d}x_n\\ & \qquad+\lambda^n\int_{\mathbb{R}^n_+}\frac{\begin{array}{l}\tilde K_A(x)-\sum_{|\alpha|\le n-1}\frac1{|\alpha|!}\partial_{x_\alpha}\tilde K_A(0)x^\alpha\\ \quad -\frac1{n!}\sum_{|\alpha|=n}\partial_{x_\alpha}\tilde K_A(0)x^\alpha\chi_{|x|\le1}\end{array}}{\left(\left\vert \bar x\right\vert^2+(x_n+\lambda{\mathfrak{D}})^2-\lambda^2\right)^n}{\rm d}\bar x{\rm d}x_n\\ & \quad=\lambda^n\left(\log\frac1\lambda+O(1)\right)\\ & \qquad\times \sum_{i=0}^{\lfloor\frac n2\rfloor}\frac{(n-3)!!}{(n-2i)!(2i)!(2i)!!(n+2i-3)!!}\partial_{x_n}^{n-2i}\Delta_{\bar x}^i\tilde K_A(0)\omega_{n-2}\int_0^\pi\sin^{n-2i}t{\rm d}t\\ & \qquad+\lambda^n\int_{\mathbb{R}^n_+}\frac{\tilde K_A(x)-\sum_{|\alpha|\le n}\frac1{|\alpha|!}\partial_{x_\alpha}\tilde K_A(0)x^\alpha\chi_{|x|\le1}}{\left(\left\vert \bar x\right\vert^2+(x_n+\lambda{\mathfrak{D}})^2-\lambda^2\right)^n}{\rm d}\bar x{\rm d}x_n\\ & \qquad+O\left(\lambda^n\sum_{j=0}^{n-1}\sum_{i=0}^{\lfloor\frac j2\rfloor}\partial_{x_n}^{j-2i}\Delta_{\bar x}^i\tilde K_A(0)\right)\\ & \quad=\lambda^n\log\frac1\lambda\sum_{i=0}^{\lfloor\frac n2\rfloor}\frac{(n-3)!!}{(n-2i)!(2i)!(2i)!!(n+2i-3)!!}\partial_{x_n}^{n-2i}\Delta_{\bar x}^i\tilde K_A(0)\omega_{n-2}\\ & \qquad\times \int_0^\pi\sin^{n-2i}t{\rm d}t(1+o(1))\\ & \qquad+\lambda^n\int_{\mathbb{R}^n_+}\frac{\tilde K_A(x)-\sum_{|\alpha|\le n}\frac1{|\alpha|!}\partial_{x_\alpha}\tilde K_A(0)x^\alpha\chi_{|x|\le1}}{\left\vert \bar x\right\vert^{2n}}{\rm d}\bar x{\rm d}x_n\\ & \qquad+\underbrace{\begin{array}{l}\displaystyle\int_{\mathbb{R}^n_+}\left(\tilde K_A(\lambda y)-\sum_{|\alpha|\le n}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{x_\alpha}\tilde K_A(0)y^\alpha\right)\\ \quad \times \displaystyle\left(\frac1{\left(|\bar y|^2+\left(y_n+{\mathfrak{D}}\right)^2-1\right)^n}-\frac1{|y|^{2n}}\right){\rm d}\bar y{\rm d}y_n\end{array}}_{=:I'''} \\ & \qquad+o\left(\sum_{j=0}^{n-1}\lambda^j\sum_{i=0}^{\lfloor\frac j2\rfloor}\partial_{x_n}^{j-2i}\Delta_{\bar x}^i\tilde K_A(0)\right)\\ & \quad=\lambda^n\log\frac1\lambda\\& \qquad \times \sum_{i=0}^{\lfloor\frac n2\rfloor}\frac{(n-3)!!}{(n-2i)!(2i)!(2i)!!(n+2i-3)!!}({-}1)^n(1+\xi_n)^n\partial_\nu^{n-2i}\Delta_\tau^i K(\xi)\omega_{n-2}\\ & \qquad\times \int_0^\pi\sin^{n-2i}t{\rm d}t(1+o(1))\\ & \qquad+\lambda^n(1+\xi_n)^n\int_{\mathbb{B}^n}\frac{K(z)-\sum_{|\alpha|\le n}\frac1{|\alpha|!}\partial_{\xi_\alpha}K(\xi)(z-\xi)^\alpha}{|z-\xi|^{2n}}{\rm d}z\\ & \qquad+ I''+o\left(\sum_{j=0}^{n-1}\lambda^j\sum_{i=0}^{\lfloor\frac j2\rfloor}\partial_\nu^{j-2i}\Delta_\tau x^iK(\xi)\right). \end{align*}

In order to iterate and find the next order terms, we again need a series expansion: we get

\begin{align*} & \frac1{\left(|\bar y|^2+\left(y_n+{\mathfrak{D}}\right)^2-1\right)^n}\\& \quad =\sum_{j=0}^\infty\frac1{|y|^{2(n+j)}}\sum_{i=0}^{\lfloor\frac j2\rfloor}({-}1)^{j-i}\frac{(n+j-i-1)!}{(n-1)!i!(j-2i)!}\left({\mathfrak{D}}^2-1\right)^i\left(2{\mathfrak{D}}\right)^{j-2i}|y|^{2i}y_n^{j-2i}, \end{align*}

which in turn comes from

\begin{align*} \frac1{at^2+bt+1}=\sum_{j=0}^\infty t^j\sum_{i=0}^{\lfloor\frac j2\rfloor}({-}1)^{j-i}\frac{(n+j-i-1)!}{(n-1)!i!(j-2i)!}a^ib^{j-2i}. \end{align*}

Therefore, for $m>n$ we get:

\begin{align*} & \lambda^m\log\frac1\lambda\sum_{i=0}^{\lfloor\frac{m-n}2\rfloor}({-}1)^{m-n-i}\frac{(m-i-1)!}{(n-1)!i!(m-n-2i)!}\left({\mathfrak{D}}^2-1\right)^i\left(2{\mathfrak{D}}\right)^{m-n-2i}\\ & \quad\times\sum_{j=0}^{\lfloor\frac m2\rfloor}\frac{(n-3)!!}{(m-2j)!(2j)!(2j)!!(n+2j-3)!!}({-}1)^m(1+\xi_n)^m\partial_\nu^{m-2j}\Delta_\tau^j K(\xi)\omega_{n-2}\\ & \quad\times\int_0^\pi\sin^{2m-n-2i-2j}t{\rm d}t(1+o(1))\\ & \quad+\lambda^m(1+\xi_n)^m\sum_{i=0}^{\lfloor\frac{m-n}2\rfloor}({-}1)^{m-n-i}\frac{(m-i-1)!}{(n-1)!i!(m-n-2i)!}\left({\mathfrak{D}}^2-1\right)^i\left(2{\mathfrak{D}}\right)^{m-n-2i} \\ & \quad\times\int_{\mathbb{B}^n}\left(K(z)-\sum_{|\alpha|\le m}\frac1{|\alpha|!}\partial_{\xi_\alpha}K(\xi)(z-\xi)^\alpha\right)\frac{|z+\xi|^{2i}\left(1-|z|^2\right)^{m-n-2i}}{|z-\xi|^{2m}}{\rm d}z\\ & \quad+\int_{\mathbb{R}^n_+}\left(\tilde K_A(\lambda y)-\sum_{|\alpha|\le m}\frac{\lambda^{|\alpha|}}{|\alpha|!}\partial_{x_\alpha}\tilde K_A(0)y^\alpha\right)\left(\frac1{\left(|\bar y|^2+\left(y_n+{\mathfrak{D}}\right)^2-1\right)^n}\right.\\ & \quad\left.-\sum_{j=0}^{m-n}\frac1{|y|^{2(n+j)}}\sum_{i=0}^{\lfloor\frac j2\rfloor}({-}1)^{j-i}\right.\\ & \quad\left.\times\frac{(n+j-i-1)!}{(n-1)!i!(j-2i)!}\left({\mathfrak{D}}^2-1\right)^i\left(2{\mathfrak{D}}\right)^{j-2i}|y|^{2i}y_n^{j-2i}\vphantom{\frac1{\left(|\bar y|^2+\left(y_n+{\mathfrak{D}}\right)^2-1\right)^n}}\right){\rm d}\bar y{\rm d}y_n\\ & \quad+o\left(\sum_{j=0}^{m-1}\lambda^j\sum_{i=0}^{\lfloor\frac j2\rfloor}\partial_\nu^{j-2i}\Delta_\tau K(\xi)\right). \end{align*}

The proof is now complete, since all the quantities are the same as in definition 2.1.

References

Abdelhedi, W., Chtioui, H. and Ahmedou, M. O.. A Morse theoretical approach for the boundary mean curvature problem on $B^4$

. J. Funct. Anal. 254 (2008), 1307–1341.CrossRef Google Scholar

Almaraz, S. M.. An existence theorem of conformal scalar flat metrics on manifolds with boundary. Pacific J. Math. 248 (2010), 1–22.CrossRef Google Scholar

Ambrosetti, A., Li, Y. Y. and Malchiodi, A.. On the Yamabe problem and the scalar curvature problems under boundary conditions. Math. Ann. 322 (2002), 667–699.CrossRef Google Scholar

Aubin, T.. Some nonlinear problems in Riemannian geometry, Springer Monographs in Mathematics (Springer-Verlag, Berlin, 1998).CrossRef Google Scholar

Battaglia, L., Cozzi, M., Fernández, A. J. and Pistoia, A.. Non-uniqueness for the nonlocal Liouville equation in $\mathbb {R}$

and applications. SIAM J. Math. Anal. 55 (2023), 4816–4842.CrossRef Google Scholar

Battaglia, L., Medina, M. and Pistoia, A.. Large conformal metrics with prescribed Gaussian and geodesic curvatures. Calc. Var. Partial Differ. Equ. 60 (2021), 39.CrossRef Google Scholar

Ben Ayed, M., El Mehdi, K. and Ahmedou, M. O.. Prescribing the scalar curvature under minimal boundary conditions on the half sphere. Adv. Nonlinear Stud. 2 (2002), 93–116.CrossRef Google Scholar

Ben Ayed, M., El Mehdi, K. and Ahmedou, M. O.. The scalar curvature problem on the four dimensional half sphere. Calc. Var. Part. Differ. Equ. 22 (2005), 465–482.CrossRef Google Scholar

Berger, M.. On Riemannian structures of prescribed Gaussian curvature for compact 2-manifolds. J. Diff. Geom. 5 (1971), 325–332.Google Scholar

Brendle, S.. A family of curvature flows on surfaces with boundary. Simon Math. Z. 241 (2002), 829–869.CrossRef Google Scholar

Brendle, S. and Chen, S. Y. S.. An existence theorem for the Yamabe problem on manifolds with boundary. J. Eur. Math. Soc. 16 (2014), 991–1016.CrossRef Google Scholar

Chang, A., Xu, X. and Yang, P.. A perturbation result for prescribing mean curvature. Math. Ann. 310 (1998), 473–496.Google Scholar

Chang, K. C. and Liu, J. Q.. A prescribing geodesic curvature problem. Math. Z. 223 (1996), 343–365.CrossRef Google Scholar

Chang, S. Y. A. and Yang, P. C.. Conformal deformation of metrics on ${\mathbb {S}}^2$

. J. Diff. Geom. 27 (1988), 259–296.Google Scholar

Chen, X., Ho, P. T. and Sun, L.. Liming prescribed scalar curvature plus mean curvature flows in compact manifolds with boundary of negative conformal invariant. Ann. Global Anal. Geom. 53 (2018), 121–150.CrossRef Google Scholar

Chen, X., Ruan, Y. and Sun, L.. The Han-Li conjecture in constant scalar curvature and constant boundary mean curvature problem on compact manifolds. Adv. Math. 358 (2019), 56.CrossRef Google Scholar

Cherrier, P.. Problemes de Neumann non lineaires sur les varietés riemanniennes. J. Funct. Anal. 57 (1984), 154–206.CrossRef Google Scholar

Chipot, M., Fila, M. and Shafrir, I.. On the solutions to some elliptic equations with nonlinear Neumann boundary conditions. Adv. Diff. Eqs. 1 (1996), 91–110.Google Scholar

Cruz-Blázquez, S., Malchiodi, A. and Ruiz, D.. Conformal metrics with prescribed scalar and mean curvature. Reine Angew. Math. 789 (2022), 211–251.CrossRef Google Scholar

Cruz-Blázquez, S. and Ruiz, D.. Prescribing Gaussian and geodesic curvatures on disks. Adv. Nonlinear Stud. 18 (2018), 453–468.CrossRef Google Scholar

Cruz-Blázquez, S., Pistoia, A. and Vaira, G., Clustering phenomena in low dimensions for a boundary Yamabe problem, https://arxiv.org/abs/2211.08219.Google Scholar

Djadli, Z., Malchiodi, A. and Ahmedou, M. O.. Prescribing Scalar and Boundary Mean Curvature on the Three Dimensional Half Sphere. J. Geom. Anal. 13 (2003), 255–289.CrossRef Google Scholar

Da Lio, F., Martinazzi, L. and Riviére, T.. Blow-Up Analysis of a Nonlocal Liouville-Type Equation. Analysis PDE 8 (2015), 1757–1805.CrossRef Google Scholar

Djadli, Z., Malchiodi, A. and Ahmedou, M. O.. The prescribed boundary mean curvature problem on $B^4$

. J. Diff. Eqs 206 (2004), 373–398.CrossRef Google Scholar

Escobar, J.. Conformal deformation of a Riemannian metric to a scalar flat metric with constant mean curvature on the boundary. Ann. Math. 136 (1992), 1–50.CrossRef Google Scholar

Escobar, J.. Conformal metrics with prescribed mean curvature on the boundary. Calc. Var. 4 (1996), 559–592.CrossRef Google Scholar

Escobar, J.. The Yamabe problem on manifolds with boundary. J. Differ. Geom. 35 (1992), 21–84.CrossRef Google Scholar

Escobar, J. and García, G.. Conformal metrics on the ball with zero scalar curvature and prescribed mean curvature on the boundary. J. Funct. Anal. 211 (2004), 71–152.CrossRef Google Scholar

Gálvez, J. A. and Mira, P.. The Liouville equation in the half-plane. J. Differ. Equ. 246 (2009), 4173–4187.CrossRef Google Scholar

Grossi, M. and Prashanth, S.. Local solutions for elliptic problems with exponential nonlinearities via finite dimensional reduction. Indiana Univ. Math. J. 54 (2005), 383–415.CrossRef Google Scholar

Guo, Y. X. and Liu, J.. Blow-up analysis for solutions of the Laplacian equation with exponential Neumann boundary condition in dimension two. Commun. Contemp. Math. 8 (2006), 737–761.CrossRef Google Scholar

Han, Z. C. and Li, Y. Y.. The existence of conformal metrics with constant scalar curvature and constant boundary mean curvature. Comm. Anal. Geom. 8 (2000), 809–869.CrossRef Google Scholar

Han, Z. C. and Li, Y. Y.. The Yamabe problem on manifolds with boundaries: existence and compactness results. Duke Math. J. 99 (1999), 489–542.CrossRef Google Scholar

Jevnikar, A., López-Soriano, R., Medina, M. and Ruiz, D.. Blow-up analysis of conformal metrics of the disk with prescribed Gaussian and geodesic curvatures. Anal. PDE 15 (2022), 1897–1931.CrossRef Google Scholar

Jiménez, A.. The Liouville equation in an annulus. Nonlinear Anal. 75 (2012), 2090–2097.CrossRef Google Scholar

Kazdan, F.W.Warner J. L.. Curvature functions for compact 2-manifolds. Ann. Math. 99 (1974), 14–47.CrossRef Google Scholar

Li, Y. Y.. Prescribing scalar curvature on $S^n$

and related problems. II. Existence and compactness. Comm. Pure Appl. Math. 49 (1996), 541–597.3.0.CO;2-A>CrossRef Google Scholar

Li, Y. and Liu, P.. A Moser-Trudinger inequality on the boundary of a compact Riemann surface. Math. Z. 250 (2005), 363–386.CrossRef Google Scholar

Li, Y. Y. and Zhu, M.. Uniqueness theorems through the method of moving spheres. Duke Math. J. 80 (1995), 383–417.CrossRef Google Scholar

Liu, P. and Huang, W.. On prescribing geodesic curvature on D2. Nonlinear Analysis 60 (2005), 465–473.Google Scholar

López-Soriano, R., Malchiodi, A. and Ruiz, D.. Conformal metrics with prescribed Gaussian and geodesic curvatures. Ann. Sci. Éc. Norm. Supér. (4) 55 (2022), 1289–1328.CrossRef Google Scholar

Marques, F. C.. Conformal deformations to scalar-flat metrics with constant mean curvature on the boundary. Comm. Anal. Geom. 15 (2007), 381–405.CrossRef Google Scholar

Marques, F. C.. Existence results for the Yamabe problem on manifolds with boundary. Indiana Univ. Math. J. (), –.Google Scholar

Mayer, M. and Ndiaye, C. B.. Barycenter technique and the Riemann mapping problem of Cherrier-Escobar. J. Differ. Geom. 107 (2017), 519–560.CrossRef Google Scholar

Ruiz, D..Conformal metrics of the disk with prescribed Gaussian and geodesic curvatures, https://arxiv.org/abs/2108.12815.Google Scholar

Xu, X. and Zhang, H.. Conformal metrics on the unit ball with prescribed mean curvature. Math. Ann. 365 (2016), 497–557.CrossRef Google Scholar

Zhang, L.. Classification of conformal metrics on $\mathbb {R}^2_+$

with constant Gauss curvature and geodesic curvature on the boundary under various integral finiteness assumptions. Calc. Var. Partial Differ. Equ. 16 (2003), 405–430.CrossRef Google Scholar

Article contents

Prescribing nearly constant curvatures on balls

Abstract

Keywords

MSC classification

1. Introduction

2. Notation and preliminaries

2.1. Conformal metrics

2.2. Solutions of the unperturbed problems

3. Properties of the energy functionals

4. The linear theory

4.1. The $2$-dimensional case

4.1.1. Rewriting the problem

4.1.2. The reduced energy

4.2. The $n$-dimensional case

4.2.1. Rewriting the problem

4.2.2. The reduced energy

5. Existence of critical points of $\Gamma$

Acknowledgements

Appendix A. Proof of proposition 3.4

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests