Published online by Cambridge University Press: 18 March 2019
Given a sequence of polynomials 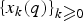 $\{x_k(q)\}_{k \ges 0}$, define the transformation
$\{x_k(q)\}_{k \ges 0}$, define the transformation
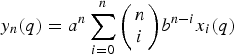 $$y_n(q) = a^n\sum\limits_{i = 0}^n {\left( \matrix{n \cr i} \right)} b^{n-i}x_i(q)$$
$$y_n(q) = a^n\sum\limits_{i = 0}^n {\left( \matrix{n \cr i} \right)} b^{n-i}x_i(q)$$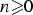 $n\ges 0$. In this paper, we obtain the relation between the Jacobi continued fraction of the ordinary generating function of yn(q) and that of xn(q). We also prove that the transformation preserves q-TPr+1 (q-TP) property of the Hankel matrix
$n\ges 0$. In this paper, we obtain the relation between the Jacobi continued fraction of the ordinary generating function of yn(q) and that of xn(q). We also prove that the transformation preserves q-TPr+1 (q-TP) property of the Hankel matrix 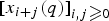 $[x_{i+j}(q)]_{i,j \ges 0}$, in particular for r = 2,3, implying the r-q-log-convexity of the sequence
$[x_{i+j}(q)]_{i,j \ges 0}$, in particular for r = 2,3, implying the r-q-log-convexity of the sequence 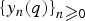 $\{y_n(q)\}_{n\ges 0}$. As applications, we can give the continued fraction expressions of Eulerian polynomials of types A and B, derangement polynomials types A and B, general Eulerian polynomials, Dowling polynomials and Tanny-geometric polynomials. In addition, we also prove the strong q-log-convexity of derangement polynomials type B, Dowling polynomials and Tanny-geometric polynomials and 3-q-log-convexity of general Eulerian polynomials, Dowling polynomials and Tanny-geometric polynomials. We also present a new proof of the result of Pólya and Szegö about the binomial convolution preserving the Stieltjes moment property and a new proof of the result of Zhu and Sun on the binomial transformation preserving strong q-log-convexity.
$\{y_n(q)\}_{n\ges 0}$. As applications, we can give the continued fraction expressions of Eulerian polynomials of types A and B, derangement polynomials types A and B, general Eulerian polynomials, Dowling polynomials and Tanny-geometric polynomials. In addition, we also prove the strong q-log-convexity of derangement polynomials type B, Dowling polynomials and Tanny-geometric polynomials and 3-q-log-convexity of general Eulerian polynomials, Dowling polynomials and Tanny-geometric polynomials. We also present a new proof of the result of Pólya and Szegö about the binomial convolution preserving the Stieltjes moment property and a new proof of the result of Zhu and Sun on the binomial transformation preserving strong q-log-convexity.