Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-18T00:16:50.884Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive solutions of certain elliptic systems with density-dependent diffusions

Published online by Cambridge University Press:  14 November 2011

Inkyung Ahn  and
Lige Li
Inkyung Ahn
Affiliation:
Department of Mathematics, Kansas State University, Manhattan, KS 66506, U.S.A
Lige Li
Affiliation:
Department of Mathematics, Kansas State University, Manhattan, KS 66506, U.S.A
Get access Rights & Permissions [Opens in a new window]

Extract

Results are obtained on the existence of positive solutions to the following elliptic system:

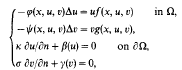
in a bounded region Ω in Rn with a smooth boundary, where the diffusion terms φ ψ are non-negative functions and the system could be degenerate, β γ are strictly increasing functions, k,σ ≧ 0 are constants. We assume also that the growth rates f, g satisfy certain monotonicities. Applications to biological interactions with density-dependent diffusions are given.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 125 , Issue 5 , 1995 , pp. 1031 - 1050
Copyright
Copyright © Royal Society of Edinburgh 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Agmon, S., A. Doughs and L. Nirenberg. Estimate near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions. I. Comm. Pure Appl. Math. 12 (1959), 623–727.CrossRefGoogle Scholar
2Amann, H.. Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces. SIAM Rev. 18 (1976), 620–709.CrossRefGoogle Scholar
3Blat, J. and Brown, K. J.. Bifurcation of steady-state solutions in predator-prey and competition systems. Proc. Roy. Soc. Edinburgh 97 (1984), 21–34.CrossRefGoogle Scholar
4Brézis, H.. Monotonicity methods in Hilbert spaces and some applications to nonlinear differential equations. In Contributions to Nonlinear Functional Analysis, 101–56 (New York: Academic Press, 1971).CrossRefGoogle Scholar
5Cañada, A. and Gámez, J. L.. Some remarks about the existence of positive solutions for elliptic systems. Proc. First World Conf. on Nonlin. Ana., Tampa, USA (to appear).Google Scholar
6Cantrell, R. S., Cosner, C. and Hutson, V.. Permanence in some diffusive Lotka-Volterra models for three interacting species. Dynam. Systems Appl. 2 (1993), 505–30.Google Scholar
7Dancer, E. N.. On the existence and uniqueness of positive solutions for competing species models with diffusion. Trans. Amer. Math. Soc. 326 (1991), 829–59.CrossRefGoogle Scholar
8Deuring, P.. An initial-boundary-value problem for a certain density-dependent diffusion system. Math.Z. 194(1987), 375–96.CrossRefGoogle Scholar
9Dorroh, J. R. and Rieder, Gisèle R.. Existence and regularity of solutions of singular quasilinear diffusion equations. In Semi. Notes in Funl. Anal, and Part. Diff. Equas. Louisiana State University (1991), 60–76.Google Scholar
10Dorroh, J. R. and Rieder, Gisele R.. A singular quasilinear parabolic problem in one space dimension. J. Differential Equations 91 (1991), 1–23.CrossRefGoogle Scholar
11Edmunds, D. E. and Evans, W. P.. Spectral Theory and Differential Operators (Oxford: Oxford Science Publications, 1987).Google Scholar
12Eilbeck, J. C., Furter, J. E. and López-Gómez, J.. Coexistence in the competition model with diffusion. J. Differential Equations (to appear).Google Scholar
13Figurado, D. G. De. Positive solution of semilinear elliptic problems. Lecture Notes in Mathematics 957(1982), 34–87.Google Scholar
14Gilbarg, D. and Trudinger, N.. Elliptic Partial Differential Equations of Second Order (Berlin: Springer, 1983).Google Scholar
15Goldstein, J. A. and Lin, C.-Y.. Singular parabolic boundary value problems in one space dimension. J. Differential Equations 68 (1987), 429–43.CrossRefGoogle Scholar
16Leung, A. and Fan, G.. Existence of positive solutions for elliptic system-degenerate and nondegenerate ecological models. J. Math. Anal. Appl. 151 (1990), 512–31.CrossRefGoogle Scholar
17Li, L. and Ghoreishi, A.. On positive solutions of general nonlinear elliptic symbiotic interacting systems. J. Appl. Anal. 14 (1991), 281–95.CrossRefGoogle Scholar
18Li, L. and Liu, Y.. Spectral and nonlinear effects in certain elliptic systems of three variables. SIAM J. Math. Anal. 24 (1993), 480–98.CrossRefGoogle Scholar
19Lin, C. Y.. Degenerate nonlinear parabolic boundary value problems. Nonlinear Anal. 13 (1989), 1303–15.CrossRefGoogle Scholar
20Lui, R.. Positive solutions of an elliptic system arising from a model in evolutionary ecology. J. Math. Biol. 29(1991), 239–50.CrossRefGoogle Scholar
21Murray, J. D.. Mathematical Biology (Berlin: Springer, 1989).CrossRefGoogle Scholar
22Pao, C. V.. Nonlinear Parabolic and Elliptic Equations (New York: Plenum Press, 1992).Google Scholar
23Ramm, A. G. and Li, L.. Estimates for Green's functions. Proc. Amer. Math. Soc. 103 (1988), 875–81.Google Scholar
24Roitt, Ivan et al. Immunology, 2nd edn (New York: Gower Medical, 1989).Google Scholar
25Ruan, W. and Feng, W.. On the fixed point index and multiple steady-state solutions of reactiondiffusion systems. J. Differential Integral Equations (to appear).Google Scholar
26Wloka, J.. Partial Differential Equations (Edinburgh: Cambridge University Press, 1987).CrossRefGoogle Scholar