Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T01:48:40.016Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive perturbations of self-adjoint Schrödinger operators

Published online by Cambridge University Press:  14 November 2011

Th. Kappeler
Th. Kappeler
Affiliation:
Department of Mathematics, University of California, Berkeley, Calif., U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper, we prove that a positive perturbation T = T0 + q (q ≧ 0 and in 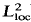) of an essentially self-adjoint Schrödinger operator T0 = −Δ + q0 on 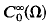is again essentially self-adjoint if T is relatively bounded with respect to T0. An application of the method of the proof to positive approximations of elements u ≧ 0 in D(T) by a positive sequence in 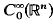is given.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 99 , Issue 3-4 , 1985 , pp. 241 - 248
Copyright
Copyright © Royal Society of Edinburgh 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Brézis, H.. “Localized” self-adjointness of Schrödinger operators. J. Operator Theory 1 (1979), 287–290.Google Scholar
2Cycon, H. L.. On the stability of self-adjointness of Schrödinger operators under positive perturbations. Proc. Roy. Soc. Edinburgh Sect. A 86 (1980), 165–175.CrossRefGoogle Scholar
3Cycon, H. L.. A theorem on “localized” self-adjointness of Schrödinger operators with potentials. Internal J. Math. 5 (1982), 545–552.Google Scholar
4Cycon, H. L.. On the form sum and the Friederichs extension of Schrödinger operators with singular potentials. J. Operator Theory 6 (1981), 75–86.Google Scholar
5Goelden, H. W.. On non-degeneracy of the ground state of Schrödinger operators. Math. Z. 155 (1977), 239–247.CrossRefGoogle Scholar
6Kato, T.. Pertubation theory for linear operators (Berlin: Springer, 1966).Google Scholar
7Kato, T.. Nonselfadjoint Schrödinger operators with singular first-order coefficients. Proc. Roy. Soc. Edinburgh Sect. A. 96, 323–329.CrossRefGoogle Scholar
8Simader, C. G.. Essential self-adjointness of Schrödinger operators bounded from below. Math. Z. 159 (1978), 47–50.CrossRefGoogle Scholar
9Wust, R.. Generalizations of Rellich's theorem on perturbation of (essentially) selfadjoint operators. Math. Z. 119 (1971), 276–280.CrossRefGoogle Scholar
10Reed, M. and Simon, B.. Modern Methods of Mathematical Physics, vol II (New York: Academic Press, 1975).Google Scholar