Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T01:48:39.465Z Has data issue: false hasContentIssue false
  • English
  • Français

Phragmén–Lindelöf theorems in slabs for some systems of non-hyperbolic second-order quasi-linear equations

Published online by Cambridge University Press:  12 July 2007

Kirk Lancaster
Kirk Lancaster
Affiliation:
Department of Mathematics and Statistics, Wichita State University, Wichita, KS 67260-0033, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose f = (f1, …, fm) is a solution of a non-hyperbolic quasi-linear system of the form with fk = φk on ∂Ω, where each fi is a bounded function in C2(Ω) ∩ C0(Ω̄). For a system of equations that can have a slightly more general form than above, when Ω is an unbounded open subset of a slab SM and 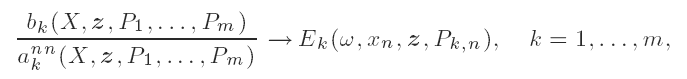as |X| → ∞ in a specified manner and when certain other conditions are satisfied, a Phragmèn–Lindelöf theorem that yields the limits at infinity of the functions fk(X), k = 1, …, m, is proven.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 133 , Issue 5 , October 2003 , pp. 1155 - 1173
Copyright
Copyright © Royal Society of Edinburgh 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)