Let Ω ⊂ RN be a smooth bounded domain. Let 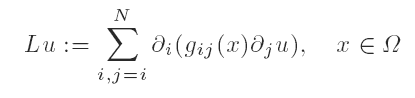be a second-order strongly elliptic differential operator with smooth symmetric coefficients. Let B denote the Dirichlet or the Neumann boundary operator. We prove the existence of a smooth potential a : Ω → R such that all sufficiently small vector fields on RN + 1 can be realized on the centre manifold of the semilinear parabolic equation 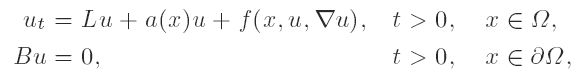by an appropriate nonlinearity f : ( x, s, w ) ∈ Ω x R x RN ↦ f ( x, s, w ) ∈ R.

For N = 2, n, k ∈ N, we prove the existence of a smooth potential a : Ω → R such that all sufficiently small k-jets of vector fields on Rn can be realized on the centre manifold of the semilinear parabolic equation 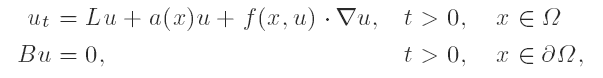by an appropriate nonlinearity f : ( x, s ) ∈ Ω x R ↦ f (x, s ) ∈ R2 ( here, ‘·’ denotes the scalar product in R2).