Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-17T23:19:50.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic solutions to second order Hamiltonian systems in an unbounded potential well*

Published online by Cambridge University Press:  14 November 2011

C. Greco
C. Greco
Affiliation:
Dipartimento di Matematica, Università Degli Studi di Bari, Bari, Italy
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper we give some results on the existence of periodic solutions to the second order Hamiltonian system:

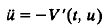
where 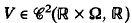and Ω is an open set of ℝn with non-empty bounded complement ℝn\Ω; we suppose V(t, x) is periodic in t, V(t, x)→ + ∞ as x → ∂Ω and V is super (or sub)-quadratic as |x| → + ∞.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 105 , Issue 1 , 1987 , pp. 1 - 15
Copyright
Copyright © Royal Society of Edinburgh 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bartolo, P., Benci, V. and Fortunate, D.Abstract critical point theorems and applications to some nonlinear problems with “strong” resonance at infinity, Nonlinear Anal. 7 (1983), 981–1012.CrossRefGoogle Scholar
2Benci, V.. Some critical point theorems and applications. Comm. Pure Appl. Math. 33 (1980), 147–172.CrossRefGoogle Scholar
3Benci, V.. A geometrical index for the group S1 and some applications to the study of periodic solutions of ordinary differential equations. Comm. Pure Appl. Math. 33 (1980), 147–172.CrossRefGoogle Scholar
4Benci, V.. Normal modes of a Lagrangian system constrained in a potential well. Ann. Inst. H. Poincaré Sect. B (N.S.) 1 (5) (1984), 379–400.Google Scholar
5Benci, V., Capozzi, A. and Fortunate, D.Periodic solutions ofHamiltonian systemsof prescribed period. MCR Tech. Summ. Rep. 2508, April 1983.Google Scholar
6Benci, V. and Rabinowitz, P. H.. Critical point theorems for indefinite functionals. Invent. Math. 52 (1979), 241–273.CrossRefGoogle Scholar
7Berestycki, H.. Solutions périodiques de systèmes Hamiltoniens. Sém. Bourbaki, 35e année, 1982–1983, 603.Google Scholar
8Cerami, G.. Un criterio di esistenza per i punti critici su varietà illimitate. Re. 1st. lomb. Sci. Lett. 112 (1978), 332–336.Google Scholar
9Gilbarg, D. and Trudinger, N. S.. Elliptic partial differential equations of second order (Berlin: Springer, 1977).Google Scholar
10Rabinowitz, P. H.. Periodic solutions of Hamiltonian systems. Comm. Pure Appl. Math. 31 (1978), 157–184.Google Scholar
11Rabinowitz, P. H.. Periodic solutions of Hamiltonian systems: a survey. SIAM J. Math. Anal. 13 (1982), 343–352.CrossRefGoogle Scholar
12Salvatore, A.. Periodic solutions of Hamiltonian systems with a subquadratic potential. Boll. Un. Mat. Ital. C 1 (1984), 393–406.Google Scholar