Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-17T00:29:41.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic solutions for one-dimensional nonlinear nonlocal problem with drift including singular nonlinearities

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  23 December 2021

Lisbeth Carrero Open the ORCID record for Lisbeth Carrero [Opens in a new window]  and
Alexander Quaas
Lisbeth Carrero
Affiliation:
Universidad Técnica Federico Santa María, Casilla V-110, Avenida España, 1680 Valparaíso, Chile ([email protected])
Alexander Quaas
Affiliation:
Departamento de Matemática, Universidad Técnica Federico Santa María, Casilla V-110, Avenida España, 1680 Valparaíso, Chile ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove existence results of a one-dimensional periodic solution to equations with the fractional Laplacian of order $s\in (1/2,1)$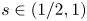, singular nonlinearity and gradient term under various situations, including nonlocal contra-part of classical Lienard vector equations, as well other nonlocal versions of classical results know only in the context of second-order ODE. Our proofs are based on degree theory and Perron's method, so before that we need to establish a variety of priori estimates under different assumptions on the nonlinearities appearing in the equations. Besides, we obtain also multiplicity results in a regime where a priori bounds are lost and bifurcation from infinity occurs.

Keywords

Periodic solutionfractional Laplaciansingular nonlinearitydegree theoryPerron's methodbifurcation from infinity

MSC classification

Primary: 35B10: Periodic solutions
Secondary: 35B09: Positive solutions 35B32: Bifurcation 35B45: A priori estimates 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 1 , February 2023 , pp. 229 - 261
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosio, V.. Regularity results for nonlocal equations by approximation. Arch. Ration. Mech. Anal. 200 (2009), 59–88.Google Scholar
Ambrosio, V.. Infinitely many periodic solutions for a fractional problem under perturbation. J. Elliptic Parabolic Equ. 2 (2016), 115–117.Google Scholar
Ambrosio, V.. Periodic solutions for a superlinear fractional problem without the Ambrosetti-Rabinowitz condition. Discrete Contin. Dyn. Syst. 37 (2017), 2265–2284.CrossRefGoogle Scholar
Ambrosio, V.. Periodic solutions for critical fractional problems. Calc. Var. Partial Differ. Equ. 57 (2018), 45.CrossRefGoogle Scholar
Ambrosio, V.. Infinitely many periodic solutions for a class of fractional Kirchhoff problems. Monatsh. Math. 190 (2019), 615–639.CrossRefGoogle Scholar
Ambrosio, V. and Bisci, G.. Periodic solutions for nonlocal fractional equations. Commun. Pure Appl. Anal. 16 (2017), 331–344.CrossRefGoogle Scholar
Bucur, C. and Valdinoci, E.. Nonlocal diffusion and applications, Lecture Notes of the Unione Matematica Italiana, Vol. 20, pp. 1–14 (Cham: Springer, 2010).Google Scholar
Buldyrev, S. V., Murphy, E. J., Prince, P. A., Viswanathan, G. M., Afanasyev, V. and Eugene Stanley, H.. Levy flight search patterns of wandering albatrosses. Nature 381 (1996), 413–415.Google Scholar
Dávila, G. and Chang-Lara, H. A.. Hölder estimates for non-local parabolic equations with critical drift. J. Differ. Equ. 260 (2014), 1–44.Google Scholar
del Mar González, M., DelaTorre, A., del Pino, M. and Wei, J.. Delaunay-type singular solutions for the fractional Yamabe problem. Math. Ann. 369 (2017), 1–23.Google Scholar
Du, Z. and Gui, C.. Further study on periodic solutions of elliptic equations with a fractional Laplacian. Nonlinear Anal. 193 (2017), 1–19.Google Scholar
Dyer, J., Humphries, N. and Queiroz, N. et al. Environmental context explains Lévy and Brownian movement patterns of marine predators. Nature 465 (2010), 1066–1069.Google Scholar
García-Melián, J., Quaas, A., Barrios, B. and Del Pezzo, L.. Symmetry results in the half space for a semi-linear fractional Laplace equation. 2017.Google Scholar
Garcia-Melian, J., Barrios, B. and Quaas, A.. Periodic solutions for the one-dimensional fractional Laplacian. J. Differ. Equ. 267 (2018), 5258–5289.Google Scholar
Huaux, A. and Forbat, F.. Détermination approchée et stabilité locale de la solution périodique d'une équation différentielle non linéaire. Mem. Publ. Soc. Sci. Arts Lett. Hainaut 76 (1962), 3–13.Google Scholar
Klafter, J. and Metzler, R.. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339 (2000), 1–77.Google Scholar
Krylov, N. V.. Lectures on elliptic and parabolic equations in Holder spaces (Providence, RI: American Mathematical Society, 1996).CrossRefGoogle Scholar
Lazer, A. C. and Solimini, S.. On periodic solutions of nonlinear differential equations with singularities. Proc. Am. Math. Soc. 99 (1987), 109–114.CrossRefGoogle Scholar
Li, B. and Zhang, G.. Anomalous vibrational energy diffusion in carbon nanotubes. J. Chem. Phys. 123 (2005), 014705.Google Scholar
Liénard, A.. Etude des oscillations entretenues. Rev. Gén. Electri. 23 (1928), 901–912, 946–954.Google Scholar
María, M., Barrios, B., De Bonis, I. and Peral, I.. Semilinear problems for the fractional Laplacian with a singular nonlinearity. Open Math. 13 (2015), 390–407.Google Scholar
Mawhin, J. and Gains, R. E.. Coincidence degree and nonlinear differential equations. Lecture Notes in Mathematics, vol. 568 (New York: Springer, 1977).Google Scholar
Mawhin, J., Nussbaum, R., Fitzpatrick, P. and Martelli, M.. Lecture on topological methods for ordinary differential equations, p. 128 (Berlin, Heidelberg: Springer, 1993).Google Scholar
Mawhin, J. and Schmitt, K.. Etude des oscillations entretenues. Res. Math. 14 (1988), 138–146.CrossRefGoogle Scholar
Mawhin, J.. Periodic solutions, workshop on nonlinear boundary value problems for ordinary differential equations an applications. Trieste, ICTP SMR/42/1, 1977.Google Scholar
Navarro, J.. Periodic solutions to pdes with fractional diffusion. Bachelor's degree thesis (University Politécnica the Cataluña, 2016).Google Scholar
Quaas, A., Chen, H. and Felmer, P.. Large solutions to elliptic equations involving fractional Laplacian. Ann. Inst. Henri Poincarć C 32 (2015), 1199–1228.Google Scholar
Viswanathan, G. M., da Luz, M. G. E., Raposo, E. P. and Stanley, E. H.. The physics of foraging: an introduction to random searches and biological encounters (Cambridge: Cambridge University Press, 2011).CrossRefGoogle Scholar
Sciunzi, B., Squassina, M., Canino, A. and Montoro, L.. Nonlocal problems with singular nonlinearity. Bull. Sci. Math. 141 (2017), 223–250.Google Scholar
Silvestre, L.. Regularity of the obstacle problem for a fractional power of the laplace operator. Commun. Pure Appl. Math. 60 (2007), 67–112.CrossRefGoogle Scholar
Silvestre, L. and Caffarelli, L. A.. The Evans-Krylov theorem for non local fully non linear equations. Ann. Math. 174 (2009), 1163–1187.Google Scholar
Tan, J., Felmer, P. and Quaas, A.. Positive solutions of the nonlinear Schrödinger equation with fractional Laplacian. Proc. R. Soc. Edinburgh: Sect. A Math. 142 (2012), 1237–1262.Google Scholar
Topp, E., Dávila, G. and Quaas, A.. Harnack inequality and its application to nonlocal eigenvalue problems in unbounded domains. ArXiv:1909.02624, 2019.Google Scholar
Zhang, J., Gui, C. and Du, Z.. Periodic solutions of a semilinear elliptic equation with a fractional Laplacian. J. Fixed Point Theory Appl. 19 (2017), 363–373.Google Scholar