Perforation conditions and almost algebraic order in Cuntz semigroups
Published online by Cambridge University Press: 18 April 2018
Abstract
For a C*-algebra A, determining the Cuntz semigroup Cu(A ⊗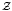 ) in terms of Cu(A) is an important problem, which we approach from the point of view of semigroup tensor products in the category of abstract Cuntz semigroups by analysing the passage of significant properties from Cu(A) to Cu(A)⊗Cu Cu(
) in terms of Cu(A) is an important problem, which we approach from the point of view of semigroup tensor products in the category of abstract Cuntz semigroups by analysing the passage of significant properties from Cu(A) to Cu(A)⊗Cu Cu(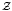 ). We describe the effect of the natural map Cu(A) → Cu(A)⊗Cu Cu(
). We describe the effect of the natural map Cu(A) → Cu(A)⊗Cu Cu(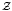 ) in the order of Cu(A), and show that if A has real rank 0 and no elementary subquotients, Cu(A)⊗Cu Cu(
) in the order of Cu(A), and show that if A has real rank 0 and no elementary subquotients, Cu(A)⊗Cu Cu(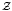 ) enjoys the corresponding property of having a dense set of (equivalence classes of) projections. In the simple, non-elementary, real rank 0 and stable rank 1 situation, our investigations lead us to identify almost unperforation for projections with the fact that tensoring with
) enjoys the corresponding property of having a dense set of (equivalence classes of) projections. In the simple, non-elementary, real rank 0 and stable rank 1 situation, our investigations lead us to identify almost unperforation for projections with the fact that tensoring with 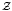 is inert at the level of the Cuntz semigroup.
is inert at the level of the Cuntz semigroup.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 148 , Issue 4 , August 2018 , pp. 669 - 702
- Copyright
- Copyright © Royal Society of Edinburgh 2018
- 1
- Cited by


