No CrossRef data available.
Article contents
Partitions with parts separated by parity: conjugation, congruences and the mock theta functions
Published online by Cambridge University Press: 30 November 2023
Abstract
Noting a curious link between Andrews’ even-odd crank and the Stanley rank, we adopt a combinatorial approach building on the map of conjugation and continue the study of integer partitions with parts separated by parity. Our motivation is twofold. Firstly, we derive results for certain restricted partitions with even parts below odd parts. These include a Franklin-type involution proving a parametrized identity that generalizes Andrews’ bivariate generating function, and two families of Andrews–Beck type congruences. Secondly, we introduce several new subsets of partitions that are stable (i.e. invariant under conjugation) and explore their connections with three third-order mock theta functions $\omega (q)$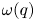 , $\nu (q)$
, $\nu (q)$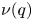 , and $\psi ^{(3)}(q)$
, and $\psi ^{(3)}(q)$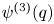 , introduced by Ramanujan and Watson.
, introduced by Ramanujan and Watson.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



