Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T01:27:25.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Pairs of positive periodic solutions of nonlinear ODEs with indefinite weight: a topological degree approach for the super–sublinear case

Part of: Nonlinear operators and their properties Qualitative theory Boundary value problems

Published online by Cambridge University Press:  16 May 2016

Alberto Boscaggin ,
Guglielmo Feltrin  and
Fabio Zanolin
Alberto Boscaggin
Affiliation:
Dipartimento di Matematica ‘Giuseppe Peano’, Università di Torino, via Carlo Alberto 10, 10123 Torino, Italy ([email protected])
Guglielmo Feltrin
Affiliation:
SISSA – International School for Advanced Studies, via Carlo Alberto 10, via Bonomea 265, 34136 Trieste, Italy ([email protected])
Fabio Zanolin
Affiliation:
Dipartimento di Matematica, Informatica e Fisica, Università di Udine, via delle Scienze 206, 33100 Udine, Italy([email protected])
Get access Rights & Permissions [Opens in a new window]

Extract

We study the periodic and Neumann boundary-value problems associated with the second-order nonlinear differential equation

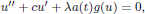
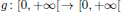where is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when

and λ > 0 is sufficiently large. Our approach is based on Mawhin's coincidence degree theory and index computations.

Keywords

boundary-value problemspositive solutionsindefinite weightmultiplicity resultscoincidence degree

MSC classification

Secondary: 34B18: Positive solutions of nonlinear boundary value problems 34C25: Periodic solutions 34B15: Nonlinear boundary value problems 47H11: Degree theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 146 , Issue 3 , June 2016 , pp. 449 - 474
Copyright
Copyright © Royal Society of Edinburgh 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)