Let f be transcendental and meromorphic in the plane and let the non-homogeneous linear differential polynomials F and G be defined by 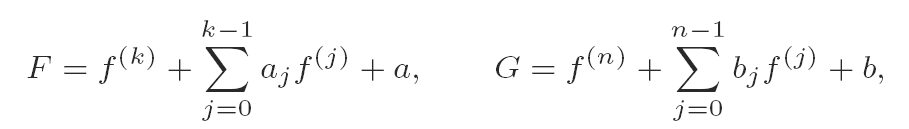where k,n ∈ N and a, b and the aj, bj are rational functions. Under the assumption that F and G have few zeros, it is shown that either F and G reduce to homogeneous linear differential polynomials in f + c, where c is a rational function that may be computed explicitly, or f has a representation as a rational function in solutions of certain associated linear differential equations, which again may be determined explicitly from the aj, bj and a and b.