Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-20T09:39:31.387Z Has data issue: false hasContentIssue false
  • English
  • Français

On the spectral analysis of self adjoint operators generated by second order difference equations

Published online by Cambridge University Press:  14 November 2011

Dale T. Smith
Dale T. Smith
Affiliation:
Department of Mathematics, University of North Texas, Denton, TX 76203, U.S.A
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper, I shall consider operators generated by difference equations of the form

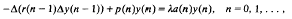
where Δ is the forward difference operator, and a, p, and r are sequences of real numbers. The connection between the oscillation constant of this equation and the bottom of the essential spectrum of self-adjoint extensions of the operator generated by the equation is given, as well as various other information about the spectrum of such extensions. In particular, I derive conditions for the spectrum to have only countably many eigenvalues below zero, and a simple criterion for the invariance of the essential spectrum.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 118 , Issue 1-2 , 1991 , pp. 139 - 151
Copyright
Copyright © Royal Society of Edinburgh 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Agmon, S.. Lectures on exponential decay of solutions of second-order elliptic equations bounds on eigenfunctions of N-body Schrödinger operators, Mathematical Notes 29 (Princeton, NJ: Princeton University Press, 1982).Google Scholar
2Atkinson, F. V.. Discrete and continuous boundary value problems, Mathematics in Science and Engineering, vol. 8 (New York: Academic Press, 1964).Google Scholar
3Blumenthal, O.. Über die entwicklung einer willkürlichen Funktion nach den Nennern des Kettenbruches für ∫∞−∞ ф(x)/(z – x) dx (Dissertation, Gottingen, 1989).Google Scholar
4Case, K. M. and Geronimo, J. S.. Scattering theory and polynomials orthogonal on the real line. Trans. Amer. Math. Soc. 258 (1980), 467–493.Google Scholar
5Chen, H.-Y.. Comparison and nonoscillation results for Volterra-Stieltjes integral equations. J. Math. Anal. Appl. 130 (1988), 257–270.CrossRefGoogle Scholar
6Chen, H.-Y.. A Levin type comparison and oscillation results for Volterra-Stieltjes integral equations. J. Math. Anal. Appl. 141 (1989), 451–462.CrossRefGoogle Scholar
7Cheng, S. S., Li, H. J. and Patula, W. T.. Bounded and zero convergent solutions of second-order difference equations. J. Math. Anal. Appl. 141 (1989), 463–483.Google Scholar
8Chihara, T. S.. An introduction to orthogonal polynomials (New York: Gordon and Breach, 1978).Google Scholar
9Chihara, T. S.. Spectral properties of orthogonal polynomials on unbounded sets. Trans. Amer. Math. Soc. 270 (1982), 623–639.Google Scholar
10Chihara, T. S.. Orthogonal polynomials with discrete spectra on the real line. J. Approx. Theory 42 (1984), 97–105.CrossRefGoogle Scholar
11Chihara, T. S.. On the spectra of certain birth and death processes. SIAM J. Appl. Math. 47 (1987), 662–669.CrossRefGoogle Scholar
12Chihara, T. S. and Nevai, P.. Orthogonal polynomials and measures with finitely many point masses. J. Approx. Theory 35 (1982), 370–380.CrossRefGoogle Scholar
13Dombrowski, J.. Orthogonal polynomials and functional analysis. In Orthogonal Polynomials: Theory and practice, ed. Nevai, P., p. 147–161 (Norwell, MA: Kluwer Academic Publishers, 1990).CrossRefGoogle Scholar
14Dombrowski, J. and Nevai, P.. Orthogonal polynomials, measures, and recurrence relations. SIAM J. Math. Anal. 17 (1986), 752–759.CrossRefGoogle Scholar
15Edmunds, E. and Evans, W. D.. Spectral Theory and Differential Operators (Oxford: Clarendon Press, 1987).Google Scholar
16Geronimo, J. S. and Nevai, P.. Necessary and sufficient conditions relating the coefficients in the recurrence formula to the spectral function for orthogonal polynomials. SIAM I. Math. Anal. 14 (1983), 622–637.CrossRefGoogle Scholar
17Glazman, I. M.. Direct Methods of Qualitative Spectral Analysis (Jerusalem: Israel Program for Scientific Translations, 1965).Google Scholar
18Hartman, P. and Putnam, C. R.. The least cluster point of the spectrum of boundary value problems. Amer. J. Math. 70 (1948), 849–855.CrossRefGoogle Scholar
19Hinton, D. B. and Lewis, R. T.. Spectral analysis of second order linear difference equations. J. Math. Anal. Appl. 63 (1978), 421–438.CrossRefGoogle Scholar
20Hooker, J. W., Kwong, M. K. and Patula, W. T.. Oscillatory second order linear difference equations and Ricatti equations. SIAM J. Math. Anal. 18 (1987), 54–63.CrossRefGoogle Scholar
21Mingarelli, A. B.. Volterra-Stieltjes Integral Equations and Generalized Ordinary Differential Expressions, Lecture Notes in Mathematics 989 (Berlin: Springer, 1983).CrossRefGoogle Scholar
22Patula, W. T.. Growth and oscillation properties of second order linear difference equations. SIAMJ. Math. Anal. 10 (1979), 55–61.CrossRefGoogle Scholar
23Patula, W. T.. Growth, oscillation, and comparison theorems for second order linear difference equations. SIAM J. Math. Anal. 10 (1979), 1272–1279.CrossRefGoogle Scholar
24Piepenbrink, J.. Nonoscillatory elliptic equations. J. Differential Equations 15 (1974), 541–550.CrossRefGoogle Scholar
25Reed, M. and Simon, B.. Methods of Modem Mathematical Physics IV: Analysis of Operators (New York: Academic Press, 1978).Google Scholar
26Reid, W. T.. Sturmian Theory for Ordinary Differential Equations, Applied Mathematical Sciences 31 (New York: Springer, 1980).CrossRefGoogle Scholar
27Simon, B.. Schrödinger Semigroups. Bull. Amer. Math. Sac. 7 (1982), 447–526.CrossRefGoogle Scholar
28Smith, D. T.. Exponential decay of resolvents of banded infinite matrices and asymptotics of linear difference equations (Dissertation, Georgia Institute of Technology, March, 1990).Google Scholar
29Stone, M. H.. Linear Transformations in Hilbert Space, American Mathematical Society Colloquium Publications 15 (New York: American Mathematical Society, 1932).Google Scholar
30van Doorn, E. A.. On oscillation properties and the interval of orthogonality of orthogonal polynomials. SIAM J. Math. Anal. 15 (1984), 1031–1042.CrossRefGoogle Scholar
31Weidmann, J.. Linear Operators in Hilbert Spaces, Graduate Texts in Mathematics 68 (New York: Springer, 1980).CrossRefGoogle Scholar