Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T01:46:20.725Z Has data issue: false hasContentIssue false
  • English
  • Français

On the spectra of non-self-adjoint realisations of second-order elliptic operators

Published online by Cambridge University Press:  14 November 2011

W. D. Evans
W. D. Evans
Affiliation:
Pure Mathematics Department, University College, Cardiff
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let τ denote the second-order elliptic expression

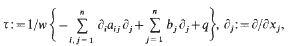
where the coefficients bj and q are complex-valued, and let Ω be a spherical shell Ω = {x:x ∈ ℝn, l <|x|<m} with l≧0, m≦∞. Under the conditions assumed on the coefficients of τ and with either Dirichlet or Neumann conditions on the boundary of Ω, τ generates a quasi-m-sectorial operator T in the weighted space L2(Ω;w). The main objective is to locate the spectrum and essential spectrum of T. Best possible results are obtained.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 90 , Issue 1-2 , 1981 , pp. 71 - 105
Copyright
Copyright © Royal Society of Edinburgh 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adams, R. A.. Sobolev spaces (New York: Academic Press, 1975).Google Scholar
2Agmon, S.. Lectures on elliptic boundary-value problems (New York: Van Nostrand, 1965).Google Scholar
3Brezis, H. and Kato, T.. Remarks on the Schrödinger operator with singular complex potentials. J. Math. Pures Appl. 58 (1979), 137–151.Google Scholar
4Dolph, C. L.. Recent developments in some non-self-adjoint problems of mathematical physics. Bull. Amer. Math. Soc. 67 (1961), 1–69.Google Scholar
5Evans, W. D.. On the essential self-adjointness of powers of Schrödinger-type operators. Proc. Roy. Soc. Edinburgh Sect. A 79 (1977), 61–77.CrossRefGoogle Scholar
6Evans, W. D.. On the J-self-adjointness of Schrödinger operators with a singular complex potential. J. London Math. Soc. 20 (1979), 495–508.CrossRefGoogle Scholar
7Evans, W. D.. On the spectra of Schrödinger operators with a complex potential. Math. Ann. 255 (1981), 57–76.Google Scholar
8Evans, W. D.. On the spectra of Schrödinger operators with a complex potential II. Proceedings of the Conference on Differential Equations, Dundee 1980. Lecture Notes in Mathematics 846 (Berlin: Springer, 1981).Google Scholar
9Evans, W. D., Kwong, M. and Zettl, T.. On the spectra of 2nth-order differential operators. Preprint.Google Scholar
10Faris, W. G.. Self-adjoint operators. Lectures Notes in Mathematics 433 (Berlin: Springer, 1975).Google Scholar
11Fortunato, D.. On the spectrum of the non-self-adjoint Schrodinger operator. Preprint.Google Scholar
12Glazman, I. M.. Direct method of qualitative spectral analysis of singular differential operators (Jerusalem: Israel Program of Scientific Translations, 1965).Google Scholar
13Hinton, D. B. and Lewis, R. T.. Discrete spectra criteria for singular differential operators with middle terms. Math. Proc. Cambridge Philos. Soc. 77 (1975), 337–347.CrossRefGoogle Scholar
14Hinton, D. B. and Lewis, R. T.. Singular differential operators with spectra discrete and bounded below. Proc. Roy. Soc. Edinburgh Sect. A 84 (1979), 117–134.Google Scholar
15Kalf, H.. On the characterization of the Friedrichs extension of ordinary or elliptic differential operators with a strongly singular potential. J. Functional Analysis 10, (1972), 230–250.Google Scholar
16Kalf, H. and Walter, J.. Strongly singular potentials and essential self-adjointness of singular elliptic operators in C(ℝn/{0}) J. Functional Analysis 10 (1972), 114–130.CrossRefGoogle Scholar
17Kato, T.. Perturbation theory for linear operators (Berlin: Springer, 1966).Google Scholar
18Kato, T.. On some Schrödinger operators with a singular complex potential. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 5 (1978), 105–114.Google Scholar
19Knowles, I.. Dissipative Sturm-Liouville operators. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 329–344.Google Scholar
20Knowles, I. and Faierman, M.. On a mixed problem for a hyperbolic equation with a discontinuity in the principal coefficients. Preprint.Google Scholar
21Knowles, I. and Race, D.. On the point spectra of complex Sturm-Liouville operators. Proc. Roy. Soc. Edinburgh Sect. A 85 (1979), 263–289.Google Scholar
22Naimark, M. A.. Linear differential operators, Pt II (New York: Ungar, 1968).Google Scholar
23Race, D.. The spectral theory of complex Sturm-Liouville operators (Ph.D. thesis, Univ. of the Witwatersrand, Johannesburg, 1979).Google Scholar
24Reed, M. and Simon, B.. Methods of modern mathematical physics IV: Analysis of Operators (New York: Academic Press, 1978).Google Scholar
25Schechter, M.. Spectra of partial differential operators (Amsterdam: North-Holland, 1971).Google Scholar