Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-28T23:07:58.256Z Has data issue: false hasContentIssue false
  • English
  • Français

On the separation property of symmetric ordinary fourth-order differential expressions

Published online by Cambridge University Press:  14 November 2011

Jyoti Das  and
Jayasri Sett
Jyoti Das
Affiliation:
Department of Pure Mathematics, Calcutta University, Calcutta 19, India
Jayasri Sett
Affiliation:
Department of Mathematics, Jogamaya Devi College, Calcutta, India
Get access Rights & Permissions [Opens in a new window]

Synopsis

Conditions are given on the coefficients p, q and r of the fourth-order, symmetric differentia expression

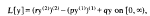
where y ∈ L2(0, ∞) and L[y] ∈ L2(0, ∞), such that some or all of the individual terms in L[y] are also in L2(0, ∞).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 86 , Issue 3-4 , 1980 , pp. 255 - 259
Copyright
Copyright © Royal Society of Edinburgh 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Everitt, W. N.. On the limit-point classification of fourth-order differential equations. J. Lond. Math. Soc. 44 (1969), 273–231.CrossRefGoogle Scholar
2Everitt, W. N. and Giertz, M.. Some properties of the domains of certain differential operators. Proc. Lond. Math. Soc. (3) 23 (1971), 301–24.CrossRefGoogle Scholar
3Everitt, W. N. and Giertz, M.. On some properties of the powers of a formally self-adjoint differential expression. Proc. Lond. Math. Soc. (3) 24 (1972), 149–170.CrossRefGoogle Scholar
4Krishna Kumar, V.. The strong limit-2 case of fourth-order differential equations. Proc. Roy. Soc. Edinburgh Sect. A 71 (1974), 297–304.Google Scholar
5Das, Jyoti and Dey, Jayasri. On the separation property of symmetric ordinary second-order differential expressions. Quaestiones Math. 1 (1976), 145–154.CrossRefGoogle Scholar