Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yang, Xiuliang
2005.
EXTENSIONS OF CLIFFORD SUBSEMIGROUPS OF THE FINITE SYMMETRIC INVERSE SEMIGROUP.
Communications in Algebra,
Vol. 33,
Issue. 2,
p.
381.
André, Jorge
Araújo, João
and
Konieczny, Janusz
2011.
Regular centralizers of idempotent transformations.
Semigroup Forum,
Vol. 82,
Issue. 2,
p.
307.
Al-Kharousi, F.
Kehinde, R.
and
Umar, A.
2016.
On the Semigroup of Partial Isometries of a Finite Chain.
Communications in Algebra,
Vol. 44,
Issue. 2,
p.
639.
Garba, G. U.
and
Imam, A. T.
2016.
Products of quasi-idempotents in finite symmetric inverse semigroups.
Semigroup Forum,
Vol. 92,
Issue. 3,
p.
645.
Dimitrova, Ilinka
and
Koppitz, Jörg
2017.
On the semigroup of all partial fence-preserving injections on a finite set.
Journal of Algebra and Its Applications,
Vol. 16,
Issue. 12,
p.
1750223.
Umar, A.
and
Zubairu, M. M.
2021.
On certain semigroups of contraction mappings of a finite chain.
Algebra and Discrete Mathematics,
Vol. 32,
Issue. 2,
p.
299.
Koppitz, J.
and
Musunthia, T.
2021.
The rank of the inverse semigroup of partial automorphisms on a finite fence.
Semigroup Forum,
Vol. 102,
Issue. 2,
p.
437.
Li, De Biao
Zhang, Wen Ting
and
Luo, Yan Feng
2022.
The monoid of orientation-preserving k-extensive transformations.
Semigroup Forum,
Vol. 104,
Issue. 2,
p.
376.
Li, De Biao
Zhang, Wen Ting
and
Luo, Yan Feng
2022.
On the monoid of all injective orientation-preserving and extensive partial transformations.
Communications in Algebra,
Vol. 50,
Issue. 1,
p.
275.
Laradji, Abdallah
and
Umar, Abdullahi
2022.
Further combinatorial results for the symmetric inverse monoid.
Algebra and Discrete Mathematics,
Vol. 33,
Issue. 2,
p.
78.
Imam, A. T.
Ibrahim, S.
Garba, G. U.
Usman, L.
and
Idris, A.
2023.
Quasi-idempotents in finite semigroup of full order-preserving transformations.
Algebra and Discrete Mathematics,
Vol. 35,
Issue. 1,
p.
62.
Dimitrova, Ilinka
and
Koppitz, Jörg
2023.
The rank of the inverse semigroup of all partial automorphisms on a finite crown.
Monatshefte für Mathematik,
Vol. 202,
Issue. 1,
p.
119.
Li, De Biao
Zhang, Wen Ting
and
Luo, Yan Feng
2023.
On certain semigroups of transformations with restricted range.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 07,
Al-Kharousi, F.
Garba, G. U.
Ibrahim, M. J.
Imam, A. T.
and
Umar, A.
2025.
On the semigroup of finite order-preserving partial injective contraction mappings.
Afrika Matematika,
Vol. 36,
Issue. 1,


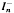 = { α ∊ SI
= { α ∊ SI