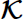Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T19:36:01.335Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of topological orbits of complex germs in classes (xy, xa + yb )

Part of: Singularities Theory of singularities and catastrophe theory

Published online by Cambridge University Press:  27 October 2016

Aldicio José Miranda ,
Liane Mendes Feitosa Soares  and
Marcelo José Saia
Aldicio José Miranda
Affiliation:
Faculdade de Matemática, Universidade Federal de Uberlândia, Campus Santa Mônica – Bloco 1F – Sala 1F120, Av. João Naves de Avila 2121, 38.408-10 Uberlândia – MG, Brazil ([email protected])
Liane Mendes Feitosa Soares
Affiliation:
Centro de Ciências da Natureza, Universidade Federal do Piaui, Av. Universitária 661, 64049-550 Teresina – PI, Brazil ([email protected])
Marcelo José Saia
Affiliation:
Departamento de Matemática, Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, Av. Trabalhador Sancarlense 400, 13566-590 São Carlos – SP, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Extract

We show that there exist an infinite number of topological orbits in 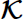classes of complex map germs from the plane to the plane that have a representative of type (xy, xa + yb ), with (a, b) ≠ = (2, 3) or (2, 5). Our key tool to prove this existence is the existence (or not) of stems in the 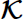class; these germs are not 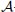-finitely determined and allow the determination of a non-finite number of topological orbits. We also show that the class (xy, x 2 + y 5) has two topological orbits.

Keywords

topological classificationinvariantsNewton non-degeneracy conditions

MSC classification

Secondary: 32S15: Equisingularity (topological and analytic) 32S05: Local singularities 32S30: Deformations of singularities; vanishing cycles 58K15: Topological properties of mappings 58K65: Topological invariants
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 147 , Issue 1 , February 2017 , pp. 205 - 224
Copyright
Copyright © Royal Society of Edinburgh 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)