Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Le Dinh, Long
and
Donal, O’regan
2022.
Notes on Convergence Results for Parabolic Equations with Riemann–Liouville Derivatives.
Mathematics,
Vol. 10,
Issue. 21,
p.
4026.
Phuong, Nguyen Duc
Baleanu, Dumitru
Agarwal, Ravi P.
and
Long, Le Dinh
2022.
Fractional evolution equation with Cauchy data in $L^{p}$ spaces.
Boundary Value Problems,
Vol. 2022,
Issue. 1,
Nguyen, Van Tien
2022.
Notes on continuity result for conformable diffusion equation on the sphere: The linear case.
Demonstratio Mathematica,
Vol. 55,
Issue. 1,
p.
952.
Nguyen, Anh Tuan
Tuan, Nguyen Huy
and
Yang, Chao
2022.
On Cauchy problem for fractional parabolic-elliptic Keller-Segel model.
Advances in Nonlinear Analysis,
Vol. 12,
Issue. 1,
p.
97.
Xu, Jiaohui
and
Caraballo, Tomas
2022.
Well-posedness of stochastic time fractional 2D-Stokes models with finite and infinite delay.
Electronic Journal of Differential Equations,
Vol. 2022,
Issue. 01-87,
p.
86.
Nguyen, Anh Tuan
and
Yang, Chao
2022.
On a time-space fractional diffusion equation with a semilinear source of exponential type.
Electronic Research Archive,
Vol. 30,
Issue. 4,
p.
1354.
Duc, Phuong Nguyen
Akdemir, Ahmet Ocak
Nguyen, Van Tien
and
Nguyen, Anh Tuan
2022.
Remarks on parabolic equation with the conformable variable derivative in Hilbert scales.
AIMS Mathematics,
Vol. 7,
Issue. 11,
p.
20020.
Binh, Tran Thanh
Thang, Bui Dinh
and
Phuong, Nguyen Duc
2023.
On initial value problem for elliptic equation on the plane under Caputo derivative.
Demonstratio Mathematica,
Vol. 56,
Issue. 1,
NGUYEN, ANH TUAN
NGHIA, BUI DAI
and
NGUYEN, VAN THINH
2023.
GLOBAL WELL-POSEDNESS OF A CAUCHY PROBLEM FOR A NONLINEAR PARABOLIC EQUATION WITH MEMORY.
Fractals,
Vol. 31,
Issue. 04,
Dai Nghia, Bui
Hoang Luc, Nguyen
Qin, Xiaolan
and
Wang, Yan
2023.
On maximal solution to a degenerate parabolic equation involving in time fractional derivative.
Electronic Journal of Applied Mathematics,
Vol. 1,
Issue. 1,
p.
62.
Huy Tuan, Nguyen
2023.
Global existence and convergence results for a class of nonlinear time fractional diffusion equation.
Nonlinearity,
Vol. 36,
Issue. 10,
p.
5144.
Xu, Jiaohui
and
Caraballo, Tomás
2023.
Existence of Weak Solutions to Nonlocal PDEs With a Generalized Definition of Caputo Derivative.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 5,
Wang, Renhai
Kinra, Kush
and
Mohan, Manil T.
2023.
Asymptotically Autonomous Robustness in Probability of Random Attractors for Stochastic Navier-Stokes Equations on Unbounded Poincaré Domains.
SIAM Journal on Mathematical Analysis,
Vol. 55,
Issue. 4,
p.
2644.
Atta, Ahmed G.
Abd‐Elhameed, Waleed M.
Moatimid, Galal M.
and
Youssri, Youssri H.
2023.
Novel spectral schemes to fractional problems with nonsmooth solutions.
Mathematical Methods in the Applied Sciences,
Vol. 46,
Issue. 13,
p.
14745.
Tri, Vo
2023.
Continuous dependence on parameters of differential inclusion using new techniques of fixed point theory.
Filomat,
Vol. 37,
Issue. 16,
p.
5469.
Vivas-Cortez, Miguel
Bibi, Maria
Muddassar, Muhammad
and
Al-Sa’di, Sa’ud
2023.
On local fractional integral inequalities via generalized
(
h
˜
1
,
h
˜
2
)
\left({\tilde{h}}_{1},{\tilde{h}}_{2})
-preinvexity involving local fractional integral operators with Mittag-Leffler kernel.
Demonstratio Mathematica,
Vol. 56,
Issue. 1,
Zhu, Yuchen
2024.
Blow-up of solutions for a time fractional biharmonic equation with exponentional nonlinear memory.
Electronic Research Archive,
Vol. 32,
Issue. 11,
p.
5988.
Wang, Renhai
Caraballo, Tomás
and
Tuan, Nguyen Huy
2024.
Mean attractors and invariant measures of locally monotone and generally coercive SPDEs driven by superlinear noise.
Journal of Differential Equations,
Vol. 381,
Issue. ,
p.
209.
Liu, Yubin
and
Peng, Li
2024.
The well-posedness analysis in Besov-type spaces for multi-term time-fractional wave equations.
Fractional Calculus and Applied Analysis,
Vol. 27,
Issue. 6,
p.
3477.
Huong, Nguyen Thi Thu
Thang, Nguyen Nhu
and
Ke, Tran Dinh
2024.
Commutator of the Caputo fractional derivative and the shift operator and applications.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 131,
Issue. ,
p.
107857.
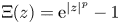 $\Xi (z)={\textrm {e}}^{|z|^{p}}-1$ and some embeddings between it and the usual Lebesgue spaces, we prove that the solution is a global-in-time solution or it shall blow up in a finite time if the initial value is regular. In the case of singular initial data, the local-in-time/global-in-time existence and uniqueness are derived. Also, the regularity of the mild solution is investigated. For the IVP associated with the second one, some modifications to the generalized formula are made to deal with the nonlinear term. We also establish some important estimates for the derivatives of resolvent operators, they are the basis for using the Picard sequence to prove the local-in-time existence of the solution.
$\Xi (z)={\textrm {e}}^{|z|^{p}}-1$ and some embeddings between it and the usual Lebesgue spaces, we prove that the solution is a global-in-time solution or it shall blow up in a finite time if the initial value is regular. In the case of singular initial data, the local-in-time/global-in-time existence and uniqueness are derived. Also, the regularity of the mild solution is investigated. For the IVP associated with the second one, some modifications to the generalized formula are made to deal with the nonlinear term. We also establish some important estimates for the derivatives of resolvent operators, they are the basis for using the Picard sequence to prove the local-in-time existence of the solution.