No CrossRef data available.
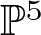 $\mathbb{P}^5$
$\mathbb{P}^5$Published online by Cambridge University Press: 16 December 2024
We denote by 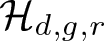 $\mathcal{H}_{d,g,r}$ the Hilbert scheme of smooth curves, which is the union of components whose general point corresponds to a smooth, irreducible, and non-degenerate curve of degree d and genus g in
$\mathcal{H}_{d,g,r}$ the Hilbert scheme of smooth curves, which is the union of components whose general point corresponds to a smooth, irreducible, and non-degenerate curve of degree d and genus g in 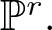 $\mathbb{P}^r.$ In this article, we study
$\mathbb{P}^r.$ In this article, we study 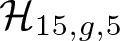 $\mathcal{H}_{15,g,5}$ for every possible genus g and determine when it is irreducible. We also study the moduli map
$\mathcal{H}_{15,g,5}$ for every possible genus g and determine when it is irreducible. We also study the moduli map 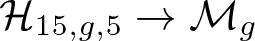 $\mathcal{H}_{15,g,5}\rightarrow\mathcal{M}_g$ and several key properties such as gonality of a general element as well as characterizing smooth elements of each component.
$\mathcal{H}_{15,g,5}\rightarrow\mathcal{M}_g$ and several key properties such as gonality of a general element as well as characterizing smooth elements of each component.