Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T22:15:42.896Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence of a saturated solution of the differential equation x′ = f (t, x)

Published online by Cambridge University Press:  14 February 2012

Johann Walter
Johann Walter
Affiliation:
Institut für Mathematik, der R.W.T.H. Aachen
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let (1) x′ = f(t, x) be any differential equation and S0 the set of solutions of (1) with open domain. It is known that for every g ∊ S0 a non-continuable (= saturated) 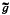∊ S0 exists which is an extension of g. Usually 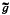is represented in the form is a sequence in S0 defined by some sort of a variant of what is called ‘recursive definition’ in set theory. It will be shown that a function

exists (P(S0) is the power set of S0) such that the above-mentioned variant can be given the form: There exists a sequence in S0 such that

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 78 , Issue 1-2 , 1977 , pp. 97 - 99
Copyright
Copyright © Royal Society of Edinburgh 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Corduneanu, C.Principles of differential and integral equations (Boston: Allyn and Bacon, 1971).Google Scholar
2Halmos, P. R.Naive set theory (Princeton: van Nostrand, 1960).Google Scholar
3Kamke, E.Differentialgleichungen I (Leipzig: Geest & Portig, 1969).Google Scholar
4Lozinski, S. M.Extending solutions of ordinary differential equations. Differential Equations 4 (1968), 620–621. Transl. from DifferentsiaVnye Uravneniya 4 (1968), 1196-1198.Google Scholar
5Reid, W. T.Ordinary differential equations (New York: Wiley, 1971).Google Scholar
6Rouche, N. and Mawhin, J.Equations différentiates ordinaires I (Paris: Masson. 1973).Google Scholar
7Walter, J. Methodical remarks on the notion of a saturated solution of the differential equation x′ = f(t, x). Colloq. Math. Soc. János Bolyai, 15, Differential Equations, Kesthely, Hungary, 1974. (Ed. Farkas, M.) 409–418. (Amsterdam: North Holland, 1977).Google Scholar