Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Everitt, W. N.
Knowles, I. W.
and
Read, T. T.
1986.
Limit-point and limit-circle criteria for Sturm-Liouville equations with intermittently negative principal coefficients.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 103,
Issue. 3-4,
p.
215.
Kauffman, Robert M.
1988.
A strong contractivity property for semigroups generated by differential operators.
Transactions of the American Mathematical Society,
Vol. 307,
Issue. 1,
p.
153.


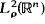 , and for all powers of
, and for all powers of 