Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-22T10:13:28.944Z Has data issue: false hasContentIssue false
  • English
  • Français

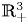On the Cauchy problem associated with the Brinkman flow in $\mathbb {R}_{+}^{3}$

Part of: Incompressible viscous fluids Partial differential equations

Published online by Cambridge University Press:  07 September 2021

Michel Molina Del Sol ,
Eduardo Arbieto Alarcon  and
Rafael José Iorio Junior
Michel Molina Del Sol
Affiliation:
Facultad de Ciencias, Departamento de Matemática, Universidad Católica del Norte (UCN), Avenida Angamos 0610, Antofagasta, Chile ([email protected])
Eduardo Arbieto Alarcon
Affiliation:
Instituto de Matemática y Estatística (IME), Universidade Federal de Goiás, Goiania, Brazil ([email protected])
Rafael José Iorio Junior
Affiliation:
Instituto Nacional de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study, we continue our study of the Cauchy problem associated with the Brinkman equations [see (1.1) and (1.2) below] which model fluid flow in certain types of porous media. Here, we will consider the flow in the upper half-space

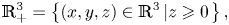\[ \mathbb{R}_{+}^{3}=\left\{\left(x,y,z\right) \in\mathbb{R}^{3}\left\vert z\geqslant 0\right.\right\}, \]
under the assumption that the plane $z=0$ is impenetrable to the fluid. This means that we will have to introduce boundary conditions that must be attached to the Brinkman equations. We study local and global well-posedness in appropriate Sobolev spaces introduced below, using Kato's theory for quasilinear equations, parabolic regularization and a comparison principle for the solutions of the problem.

Keywords

Cauchy problemintegral-differential nonlinear evolution equationslocal and global well-posednesspartial differential equations

MSC classification

Primary: 35A01: Existence problems
Secondary: 35B51: Comparison principles 76D07: Stokes and related (Oseen, etc.) flows
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 5 , October 2022 , pp. 1089 - 1108
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alarcon, E. A. and Iório, R. J. Jr. On the Cauchy problem associated to the Brinkman flow: the one dimensional theory. Mat. Contemp. Soc. Bras. Mat. 27 (2004), 1–17.Google Scholar
Auriault, J.-L.. On the domain of validity of Brinkman's equation. Transp. Porous Media 79 (2009), 215–223.CrossRefGoogle Scholar
Brinkman, H. C.. Brownian motion in a field of force and the diffusion theory. Physica 22 (1956), 29–34.Google Scholar
Churchill, R. V.. Fourier series and boundary value problems, 2nd edn (New York: McGraw-Hill Book Company, 1968).Google Scholar
Cordes, H. O.. Pseudo-differential operators on a half-line. J. Math. Mech. 18 (1969), 893–908.Google Scholar
Cordes, H. O.. Elliptic pseudo-differential operators-an abstract theory, Lecture Notes in Mathematics (Berlin: Springer-Verlag, 1979).CrossRefGoogle Scholar
Durlofsky, L. and Brady, J. F.. Analysis of the Brinkman equation as a model for flow in porous media. Phys. Fluids 30 (1987), 11.CrossRefGoogle Scholar
Fuchsberger, J.. Incorporation of obstacles in a flow using a Navier–Stokes–Brinkman penalization approach. Fluid Dyn. (2021).CrossRefGoogle Scholar
Iorio, R. J., Jr. Unique continuation principles for some equations of Benjamin-ono type. Progr. Nonlinear Differ. Equ. Their Appl. 54 (2003), 163–179.Google Scholar
Iorio, R. J., Jr. and Iorio, V. M.. Fourier analysis and partial differential equations, Cambridge Studies in Advanced Mathematics (New York: Cambridge University Press, 2001).Google Scholar
Iorio, R. J., Jr. Linares, F. and Scialom, M. A. G.. KDV and BO equations with Bore-like data. Differ. Integr. Equ. 11 (1998), 895–915.Google Scholar
Iorio, R. J., Jr. On Kato's theory of quasilinear equations, Segunda Jornada de EDP e Análise Numérica, pp. 153–178 (Rio de Janeiro, Brasil: Publicação do IMUFRJ, 1996).Google Scholar
Iorio, R. J., Jr. Functional analytic methods for partial differential equations. In KdV, BO and Friends in Weighted Sobolev Spaces (ed. H. Fujita, T. Ikebe and S. T. Kuroda). Lecture Notes in Mathematics (Berlin: Springer, 2006).Google Scholar
Johari, V.. When is Brinkman Equation selected over Darcy Law during flow through porous media?, https://www.researchgate.net/post/When_is_Brinkman_Equation_selected_over_Darcy_Law_during_flow_through_porous_media.Google Scholar
Kato, T.. Perturbation theory for linear operators. 2nd edn (Berlin: Springer-Verlag, 1966).Google Scholar
Kato, T. and Fujita, H.. On the Navier–Stokes initial value problem. Arch. Ration. Mech. Anal. 16 (1964), 269–315.Google Scholar
Kato, T. and Ponce, G.. Commutator estimates and Euler and Navier–Stokes equations. Commun. Pure Appl. Math. 41 (1988), 891–907.CrossRefGoogle Scholar
Kato, T.. Abstract evolution equations, linear and quasilinear, revisited. In Functional analysis and related topics, 1991 (ed. H. Komatsu), vol. 1540, pp. 103–127, Lecture Notes in Mathematics (Berlin: Springer, 1993).CrossRefGoogle Scholar
Kato, T.. Quasilinear equations of evolution, with applications to partial differential equations, Lecture Notes in Mathematics, vol. 448, pp. 25–70 (Berlin: Springer, 1975).CrossRefGoogle Scholar
Kato, T.. On the Cauchy problem for the (generalized) Korteweg-de Vries equation, Advances in Math. Suppl. Stud. Vol. 8, pp. 93–128 (New York: Academic Press, 1983).Google Scholar
Liu, H. et al. Parallel plates packed with regular square arrays of cylinders. Entropy 9 (2007), 118–131.10.3390/e9030118CrossRefGoogle Scholar
Mansu, G. M.. Flow in fractured media: A Darcy-Stokes-Brinkman Modelling Approach, Master Thesis in Applied Earth Sciences (Netherlands: Department of Geosciences and Engineering, 2018).Google Scholar
Molina Del Sol, M., Alarcon, E. A., Iorio, R. J., Jr. On the Cauchy problem associated to the Brinkman flow in $R^{n}$. Appl. Anal. Discrete Math. 6 (2012), 214–237.CrossRefGoogle Scholar
Molina Del Sol, M.. Two Cauchy problems associated to the brinkman flow, Serie C – Teses de Doutorado do IMPA/2011, Serie – C 127/2011, IMPA, Rio de Janeiro, Brazil, 2011.Google Scholar
Mosharaf-Dehkordi, M.. A fully coupled porous media and channels flow approach for simulation of blood and bile flow through the liver lobules. Comput. Methods Biomech. Biomed. Eng. 22 (2019), 901–915.Google ScholarPubMed
Pazy, A.. Semigroups of linear operators and applications to partial differential equations (New York: Springer Verlag, 1983).CrossRefGoogle Scholar
Reed, M. and Simon, B.. Methods of Modern Mathematical Physics, vol. I (San Diego: Academic Press, 1972).Google Scholar
Reed, M. and Simon, B.. Modern Methods of Mathematical Physics, vol. II (San Diego: Academic Press, 1975).Google Scholar
Reed, M. and Simon, B.. Modern Methods of Mathematical Physics, vol. IV (San Diego: Academic Press, 1977).Google Scholar
Schecter, M.. Modern methods in partial differential equations: An introduction (New York: McGraw-Hill, 1977).Google Scholar
Weissler, F. B.. The Navier–Stokes initial value problem in Lp. Arch. Ration. Mech. Anal. 74 (1980), 219–230.CrossRefGoogle Scholar
Wiwatanapataphee, B.. Modelling of non-Newtonian blood flow through stenosed arteries, dynamics of continuous. Discrete Impuls. Syst. Ser. B: Appl. Algorithms 15 (2008), 619–634.Google Scholar
Xie, X.. Uniformly finite element methods for Darcy–Stokes–Brinkman. Models J. Comput. Math. 26 (2008), 437–455.Google Scholar
Xu, X.. A new divergence-free interpolation operator with application, 2009.Google Scholar
Yosida, K.. Functional analysis (Berlin: Springer-Verlag, 1966).Google Scholar