Let A be a real (non-associative) algebra which is normed as real vector space, with a norm ‖·‖ deriving from an inner product and satisfying ‖ac‖ ≤ ‖a‖‖c‖ for any a,c ∈ A. We prove that if the algebraic identity (a((ac)a))a = (a2c)a2 holds in A, then the existence of an idempotent e such that ‖e‖ = 1 and ‖ea‖ = ‖a‖ = ‖ae‖, a ∈ A, implies that A is isometrically isomorphic to ℝ, ℂ, ℍ, 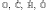or ℙ. This is a non-associative extension of a classical theorem by Ingelstam. Finally, we give some applications of our main result.