Hostname: page-component-f554764f5-fnl2l Total loading time: 0 Render date: 2025-04-12T19:50:17.229Z Has data issue: false hasContentIssue false
  • English
  • Français

On singular differential operators with positive coefficients

Published online by Cambridge University Press:  14 November 2011

Bernd Schultze
Bernd Schultze
Affiliation:
Fachbereich Mathematik, Universität Essen, Essen, Germany
Get access Rights & Permissions [Opens in a new window]

Synopsis

A class of singular real formally self-adjoint differential expressions M on I = [a, = ∞) (a ∈ ℝ), i.e. expressions of the form My = 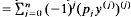with pj ≧ 0 (j = 0, …, n – 1), pn > 0 is constructed with the following property: For every integer k with 0 ≦ k < n/2 there exists an expression M in this class such that the deficiency index of T0(M) – the minimal operator associated with M – is n + 2k. This generalises a result in [3] and proves part of the McLeod's conjecture.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 120 , Issue 3-4 , 1992 , pp. 361 - 365
Copyright
Copyright © Royal Society of Edinburgh 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1Glazmann, I.. On the deficiency index of differential operators. Dokl. Akad. Nauk SSSR 64 No. 2 (1949).Google Scholar
2Kauffman, R. M.. On the limit-n classification of ordinary differential operators with positive coefficients. Proc. London Math. Soc. (3) 35 (1977), 496–526.CrossRefGoogle Scholar
3Paris, R. B. and Wood, A. D.. On the L 2 nature of solutions of nth order symmetric differential equations and McLeod's conjecture. Proc. Roy. Soc. Edinburgh Sect. A 90 (1981), 209–236.CrossRefGoogle Scholar
4Schultze, B.. Spectral properties of not necessarily self-adjoint linear differential operators. Adv. in Math. 83 No. 1 (1990), 75–95.CrossRefGoogle Scholar
5Weyl, H.. Über gewöhnliche Differentialgleichungen mit Singularitäten und die zugehörigen Entwocklungen willkürlicher Funktionen. Math. Ann. 68 (1910), 220–269.CrossRefGoogle Scholar