Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T02:08:35.889Z Has data issue: false hasContentIssue false
  • English
  • Français

On prespectrality of generalised derivations*

Published online by Cambridge University Press:  14 November 2011

Milan Hladnik
Milan Hladnik
Affiliation:
E. K. University of Ljubljana, Institute of Mathematics, Physics and Mechanics, Jadranska 19, 61000 Ljubljana, Yugoslavia
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper it is proved that, for scalar-type operators a and b on an infinite dimensional separable complex Hilbert space H, the generalised derivation Δa,b, defined for bounded linear operators x onℋ by the equation Δa,bx = ax − xb, is a (scalar-type) prespectral operator of the class 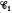(the trace class operators on ℋ) if and only if at least one of the spectra σ(a)or σ(b)is finite. It is shown also that the same condition is necessary and sufficient for Δa,b restricted to any one of the von Neumann-Schatten classes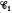(p≠2) to be a spectral operator (of scalar type). Our results may be compared with those of J. Anderson and C. Foiaş, who established in [1] that, for scalar-type a, b, Δa,b is a (scalar-type) spectral operator if and only if both spectra, σ(a) and σ(b), are finite. However, we use different and more direct methods to show the existence or nonexistence of the spectral resolution of identity for Δa,b.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 104 , Issue 1-2 , 1986 , pp. 93 - 106
Copyright
Copyright © Royal Society of Edinburgh 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Anderson, J. and Foiaş, C.,. Properties which normal operators share with normal derivations and related operators. Pacific J. Math. 61 (1975), 313–325.CrossRefGoogle Scholar
2Berkson, E., Fleming, R. J. and Jamison, J.. Groups of Isometries on certain ideals of Hilbert space operators. Math. Ann. 220 (1976), 151–156.CrossRefGoogle Scholar
3Berkson, E., Fleming, R. J., Goldstein, J. A. and Jamison, J.. One parameter groups of isometries on Cp. Rev. Roumaine Math. Pures Appl. 24 (1979), 863–868.Google Scholar
4Diestel, J. and Uhl, J. J. Jr., Vector Measures. Mathematical Surveys 15 (Amer. Math. Soc, 1977).Google Scholar
5Dowson, H. R.. Spectral Theory of Linear Operators (London-New York-San Francisco: Academic Press, 1978).Google Scholar
6Dunford, N. and Schwartz, J. T.. Linear Operators, part II: Spectral Theory (New York-London: Interscience, 1963).Google Scholar
7Dunford, N. and Schwartz, J. T.. Linear Operators, part III: Spectral Operators (New York-London-Sydney-Toronto: Wiley-Interscience, 1971).Google Scholar
8Fialkow, L. A.. A note on norm ideals and the operator X → AX-XB. Israel J. Math. 32 (1979), 331–348.CrossRefGoogle Scholar
9Gohberg, I. C. and Krein, M. G.. Introduction to the Theory of Linear Nonselfadjoint Operators. Trans. Math. Monographs 18 (Providence, R. I.: Amer. Math. Soc, 1969).Google Scholar
10Lumer, G. and Rosenblum, M.. Linear operator equations. Proc. Amer. Math. Soc. 10 (1959), 32–41.CrossRefGoogle Scholar
11Schatten, R.. Norm Ideals of Completely Continuous Operators. Ergeb. Math. Grenzgeb. (Berlin: Springer, 1960).Google Scholar
12Sourour, A. R.. Isometries of norm ideals of compact operators. J. Funct. Anal. 43 (1981), 69–77.CrossRefGoogle Scholar