Published online by Cambridge University Press: 11 July 2023
We study the existence of large solutions for nonlocal Dirichlet problems posed on a bounded, smooth domain, associated with fully nonlinear elliptic equations of order $2\,s$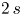 , with $s\in (1/2,\,1)$
, with $s\in (1/2,\,1)$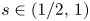 , and a coercive gradient term with subcritical power $0< p<2\,s$
, and a coercive gradient term with subcritical power $0< p<2\,s$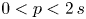 . Due to the nonlocal nature of the diffusion, new blow-up phenomena arise within the range $0< p<2\,s$
. Due to the nonlocal nature of the diffusion, new blow-up phenomena arise within the range $0< p<2\,s$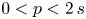 , involving a continuum family of solutions and/or solutions blowing-up to $-\infty$
, involving a continuum family of solutions and/or solutions blowing-up to $-\infty$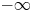 on the boundary. This is in striking difference with the local case studied by Lasry–Lions for the subquadratic case $1< p<2$
on the boundary. This is in striking difference with the local case studied by Lasry–Lions for the subquadratic case $1< p<2$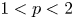 .
.