Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-25T02:43:28.277Z Has data issue: false hasContentIssue false
  • English
  • Français

On inscribed trapezoids and affinely 3-regular maps

Part of: Classical differential geometry Differential topology

Published online by Cambridge University Press:  12 May 2023

Florian Frick  and
Michael Harrison Open the ORCID record for Michael Harrison [Opens in a new window]
Florian Frick
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, Pennsylvania 15213, United States Institute of Mathematics, Freie Universität Berlin, Arnimallee 2, 14195 Berlin, Germany ([email protected])
Michael Harrison
Affiliation:
Institute for Advanced Study, 1 Einstein Drive, Princeton, New Jersey 08540, United States ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that any embedding $\mathbb {R}^d \to \mathbb {R}^{2d+2^{\gamma (d)}-1}$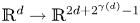 inscribes a trapezoid or maps three points to a line, where $2^{\gamma (d)}$ 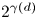is the smallest power of $2$ 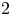satisfying $2^{\gamma (d)} \geq \rho (d)$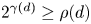, and $\rho (d)$ 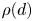denotes the Hurwitz–Radon function. The proof is elementary and includes a novel application of nonsingular bilinear maps. As an application, we recover recent results on the nonexistence of affinely $3$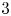-regular maps, for infinitely many dimensions $d$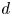, without resorting to sophisticated algebraic techniques.

Keywords

inscribed trapezoidsk-regular mapsnonsingular bilinear mapsHurwitz–Radon function

MSC classification

Primary: 53A07: Higher-dimensional and -codimensional surfaces in Euclidean $n$-space
Secondary: 57R40: Embeddings
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 4 , August 2024 , pp. 1024 - 1032
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adams, J. F.. Vector fields on spheres. Ann. Math. 75 (1962), 603–632.10.2307/1970213CrossRefGoogle Scholar
Aslam, J., Chen, S., Frick, F., Saloff-Coste, S., Setiabrata, L. and Thomas, H.. Splitting loops and necklaces: variants of the square peg problem. Forum Math. Sigma 8 (2020), E5.10.1017/fms.2019.51CrossRefGoogle Scholar
Berger, M. and Friedland, S.. The generalized Radon–Hurwitz numbers. Compos. Math. 59 (1986), 113–146.Google Scholar
Blagojević, P. V. M., Cohen, F. R., Crabb, M. C., Lück, W. and Ziegler, G. M.. Equivariant cohomology of configuration spaces mod 2: the state of the art (Cham: Springer, 2021).10.1007/978-3-030-84138-6CrossRefGoogle Scholar
Borsuk, K.. On the $k$-independent subsets of the Euclidean space and of the Hilbert space. Bull. Acad. Polon. Sci. Cl. III 5 (1957), 351–356.Google Scholar
Bogatyi, S. A.. $k$-Regular maps into Euclidean spaces and the Borsuk-Boltyanskii problem. Sbornik Math. 193 (2002), 73.10.1070/SM2002v193n01ABEH000620CrossRefGoogle Scholar
Boltyansky, V. G., Ryzhkov, S. S. and Shashkin, Yu. A.. On k-regular embeddings and their applications to the theory of approximation of functions. Usp. Mat. Nauk 15 (1960), 125–132.Google Scholar
Buczyński, J., Januszkiewicz, T., Jelisiejew, J. and Michałek, M.. Constructions of $k$-regular maps using finite local schemes. J. Eur. Math. Soc. 21 (2019), 1775–1808.10.4171/jems/873CrossRefGoogle Scholar
Chisholm, M. E.. $k$-regular mappings of $2^n$-dimensional Euclidean space. Proc. Am. Math. Soc. 74 (1979), 187–190.Google Scholar
Cohen, F. R. and Handel, D.. $k$-regular embeddings of the plane. Proc. Am. Math. Soc. 72 (1978), 201–204.Google Scholar
Frick, F. and Harrison, M.. Coupled embeddability. Bull. London Math. Soc. 54 (2022), 1609–1629.10.1112/blms.12646CrossRefGoogle Scholar
Frick, F. and Harrison, M.. Spaces of embeddings: nonsingular bilinear maps, chirality, and their generalizations. Proc. Am. Math. Soc. 150 (2022), 423–437.Google Scholar
Greene, J. and Lobb, A.. The rectangular peg problem. Ann. Math. 194 (2021), 509–517.10.4007/annals.2021.194.2.4CrossRefGoogle Scholar
Handel, D.. Obstructions to $3$-regular embeddings. Houston J. Math. 5 (1979), 339–343.Google Scholar
Handel, D.. Some existence and nonexistence theorems for $k$-regular maps. Fundam. Math. 109 (1980), 229–233.10.4064/fm-109-3-229-233CrossRefGoogle Scholar
Handel, D.. $2k$-regular maps on smooth manifolds. Proc. Am. Math. Soc. 124 (1996), 1609–1613.10.1090/S0002-9939-96-03179-6CrossRefGoogle Scholar
Handel, D. and Segal, J.. On $k$-regular embeddings of spaces in Euclidean space. Fundam. Math. 106 (1980), 231–237.10.4064/fm-106-3-231-237CrossRefGoogle Scholar
Harrison, M.. Skew flat fibrations. Math. Z. 282 (2016), 203–221.10.1007/s00209-015-1538-0CrossRefGoogle Scholar
Harrison, M.. Introducing totally nonparallel immersions. Adv. Math. 374 (2020), 251–286.10.1016/j.aim.2020.107337CrossRefGoogle Scholar
Harrison, M.. Fibrations of $\mathbb {R}^3$ by oriented lines. Algebr. Geom. Topol. 21 (2021), 2899–2928.10.2140/agt.2021.21.2899CrossRefGoogle Scholar
Hopf, H.. Ein toplogischer Beitrag zur reellen algebra. Comment. Math. Helv. 13 (1940), 219–239.10.1007/BF01378062CrossRefGoogle Scholar
James, I. M.. Euclidean models of projective spaces. Bull. London Math. Soc. 3 (1971), 257–276.10.1112/blms/3.3.257CrossRefGoogle Scholar
James, I. M.. On the immersion problem for real projective spaces. Bull. Am. Math. Soc. 69 (1963), 231–238.10.1090/S0002-9904-1963-10930-1CrossRefGoogle Scholar
Lam, K. Y.. Construction of nonsingular bilinear maps. Topology 6 (1967), 423–426.10.1016/0040-9383(67)90001-8CrossRefGoogle Scholar
Lam, K. Y.. On bilinear and skew-linear maps that are nonsingular. Q. J. Math. 19 (1968), 281–288.10.1093/qmath/19.1.281CrossRefGoogle Scholar
Lam, K. Y.. Non-singular bilinear maps and stable homotopy classes of spheres. Math. Proc. Cambridge Philos. Soc. 82 (1977), 419–425.10.1017/S0305004100054086CrossRefGoogle Scholar
Lam, K. Y.. Some interesting examples of nonsingular bilinear maps. Topology 16 (1977), 185–188.10.1016/0040-9383(77)90018-0CrossRefGoogle Scholar
Lam, K. Y.. KO-equivalences and existence of nonsingular bilinear maps. Pac. J. Math. 82 (1979), 145–154.10.2140/pjm.1979.82.145CrossRefGoogle Scholar
Lam, K. Y.. Some new results on composition of quadratic forms. Invent. Math. 79 (1985), 467–474.10.1007/BF01388517CrossRefGoogle Scholar
Ovsienko, V. and Tabachnikov, S.. On fibrations with flat fibres. Bull. London Math. Soc. 45 (2013), 625–632.10.1112/blms/bds116CrossRefGoogle Scholar
Ovsienko, V. and Tabachnikov, S.. Hopf fibrations and Hurwitz–Radon numbers. Math. Intell. 38 (2016), 11–18.10.1007/s00283-015-9618-xCrossRefGoogle Scholar