Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:42:24.193Z Has data issue: false hasContentIssue false
  • English
  • Français

On commuting approximation properties of Banach spaces

Published online by Cambridge University Press:  26 May 2009

Eve Oja  and
Indrek Zolk
Eve Oja
Affiliation:
Faculty of Mathematics and Computer Science, Tartu University, J. Liivi 2, 50409 Tartu, Estonia ([email protected]; [email protected])
Indrek Zolk
Affiliation:
Faculty of Mathematics and Computer Science, Tartu University, J. Liivi 2, 50409 Tartu, Estonia ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let a, c ≥ 0 and let B be a compact set of scalars. We show that if X is a Banach space such that the canonical projection π from X*** onto X* satisfies the inequality

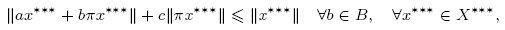
and 1 ≤ λ < max |B| + c, then every λ-commuting bounded compact approximation of the identity of X is shrinking. This generalizes a theorem by Godefroy and Saphar from 1988. As an application, we show that under the conditions described above both X and X* have the metric compact approximation property (MCAP). Relying on the Willis construction, we show that the commuting MCAP does not imply the approximation property.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 139 , Issue 3 , June 2009 , pp. 551 - 565
Copyright
Copyright © Royal Society of Edinburgh 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)