We are concerned with a Cauchy problem for the semilinear heat equation

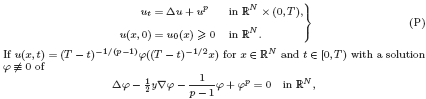
then u is called a backward self-similar solution blowing up at t = T. Let pS and pL be the Sobolev and the Lepin exponents, respectively. It was shown by Mizoguchi (J. Funct. Analysis257 (2009), 2911–2937) that k ≡ (p − 1)−1/(p−1) is a unique regular radial solution of (P) if p > pL. We prove that it remains valid for p = pL. We also show the uniqueness of singular radial solution of (P) for p > pS. These imply that the structure of radial backward self-similar blow-up solutions is quite simple for p ≥ pL.