Published online by Cambridge University Press: 28 December 2022
In this work, we study a quasilinear elliptic problem involving the 1-Laplacian operator, with a discontinuous, superlinear and subcritical nonlinearity involving the Heaviside function $H(\cdot - \beta )$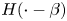 . Our approach is based on an analysis of the associated p-Laplacian problem, followed by a thorough analysis of the asymptotic behaviour or such solutions as $p \to 1^+$
. Our approach is based on an analysis of the associated p-Laplacian problem, followed by a thorough analysis of the asymptotic behaviour or such solutions as $p \to 1^+$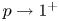 . We study also the asymptotic behaviour of the solutions, as $\beta \to 0^+$
. We study also the asymptotic behaviour of the solutions, as $\beta \to 0^+$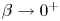 and we prove that it converges to a solution of the original problem, without the discontinuity in the nonlinearity.
and we prove that it converges to a solution of the original problem, without the discontinuity in the nonlinearity.