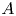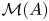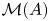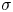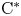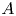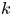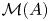1. Introduction
The study of regularity properties of multiplier algebras appears throughout the literature; see, for example, [Reference Elliott16, Reference Kaftal, Ng and Zhang22, Reference Larsen and Osaka29, Reference Perera36, Reference Rørdam42]. One notable instance of this is the study of pure infiniteness and, more concretely, of when a $\mathrm {C}^*$![]() -algebra has a purely infinite multiplier algebra; see [Reference Kaftal, Ng and Zhang23, Reference Kucerovsky, Ng and Perera27, Reference Kucerovsky and Perera28, Reference Lin30, Reference Lin32]. When this condition is relaxed to weak pure infiniteness (in the sense of [Reference Kirchberg and Rørdam25]) it was shown in [Reference Kirchberg and Rørdam25, Proposition 4.11] that a $\mathrm {C}^*$
-algebra has a purely infinite multiplier algebra; see [Reference Kaftal, Ng and Zhang23, Reference Kucerovsky, Ng and Perera27, Reference Kucerovsky and Perera28, Reference Lin30, Reference Lin32]. When this condition is relaxed to weak pure infiniteness (in the sense of [Reference Kirchberg and Rørdam25]) it was shown in [Reference Kirchberg and Rørdam25, Proposition 4.11] that a $\mathrm {C}^*$![]() -algebra is weakly purely infinite if and only if its multiplier algebra is. In general, given a certain property $\mathcal {P}$
-algebra is weakly purely infinite if and only if its multiplier algebra is. In general, given a certain property $\mathcal {P}$![]() , one can ask: If a $\mathrm {C}^*$
, one can ask: If a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() satisfies $\mathcal {P}$
satisfies $\mathcal {P}$![]() , when does $\mathcal {M}(A)$
, when does $\mathcal {M}(A)$![]() satisfy $\mathcal {P}$
satisfy $\mathcal {P}$![]() ? For example, Brown and Pedersen conjecture in [Reference Brown and Pedersen8] that the multiplier algebra of a real rank zero $\mathrm {C}^*$
? For example, Brown and Pedersen conjecture in [Reference Brown and Pedersen8] that the multiplier algebra of a real rank zero $\mathrm {C}^*$![]() -algebra with trivial $K_1$
-algebra with trivial $K_1$![]() -group is again of real rank zero; see also [Reference Lin31] and [Reference Zhang56].
-group is again of real rank zero; see also [Reference Lin31] and [Reference Zhang56].
In this paper, we study the question above for the property of being nowhere scattered (see paragraph 2.1). This notion ensures sufficient noncommutativity of the algebra, and can be characterized in a number of ways. As shown in [Reference Thiel and Vilalta49, Theorem 3.1], a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() is nowhere scattered if and only if it has no nonzero elementary ideal-quotients. This is in turn equivalent to no hereditary sub-$\mathrm {C}^*$
is nowhere scattered if and only if it has no nonzero elementary ideal-quotients. This is in turn equivalent to no hereditary sub-$\mathrm {C}^*$![]() -algebra of $A$
-algebra of $A$![]() admitting a one-dimensional representation. Every weakly purely infinite $\mathrm {C}^*$
admitting a one-dimensional representation. Every weakly purely infinite $\mathrm {C}^*$![]() -algebra is nowhere scattered ([Reference Thiel and Vilalta49, Example 3.3]) but, in contrast to the weakly purely infinite case, the multiplier algebra of a nowhere scattered $\mathrm {C}^*$
-algebra is nowhere scattered ([Reference Thiel and Vilalta49, Example 3.3]) but, in contrast to the weakly purely infinite case, the multiplier algebra of a nowhere scattered $\mathrm {C}^*$![]() -algebra need not be nowhere scattered; see examples 5.2 and 5.3.
-algebra need not be nowhere scattered; see examples 5.2 and 5.3.
Question 1.1 Let $A$![]() be nowhere scattered. When is $\mathcal {M}(A)$
be nowhere scattered. When is $\mathcal {M}(A)$![]() nowhere scattered?
nowhere scattered?
One of the motivations behind question 1.1 is the study of when a multiplier algebra has no characters, since such a property leads to important structure results. For instance, it follows from [Reference Robert39, Theorem 3.2] that every element in a nowhere scattered multiplier algebra can be written as the finite sum of commutators and products of two commutators. Moreover, nowhere scatteredness for unital $\mathrm {C}^*$![]() -algebras is related to the existence of full, square-zero elements [Reference Thiel and Vilalta51, Theorem 3.6(3)]. Thus, knowing that $\mathcal {M}(A)$
-algebras is related to the existence of full, square-zero elements [Reference Thiel and Vilalta51, Theorem 3.6(3)]. Thus, knowing that $\mathcal {M}(A)$![]() is nowhere scattered would have implications on its unitary group; see [Reference Chand and Robert11, Section 3].
is nowhere scattered would have implications on its unitary group; see [Reference Chand and Robert11, Section 3].
Nowhere scatteredness of a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() can also be characterized in terms of its Cuntz semigroup $\operatorname {Cu} (A)$
can also be characterized in terms of its Cuntz semigroup $\operatorname {Cu} (A)$![]() , a powerful invariant for $\mathrm {C}^*$
, a powerful invariant for $\mathrm {C}^*$![]() -algebras introduced in [Reference Cuntz15] and further developed in [Reference Coward, Elliott and Ivanescu14]; see also [Reference Antoine, Perera, Robert and Thiel2, Reference Antoine, Perera and Thiel3, Reference Gardella and Perera21, Reference Kirchberg and Rørdam25, Reference Rørdam43, Reference Thiel and Vilalta50, Reference Vilalta53]. Explicitly, it was shown in [Reference Thiel and Vilalta49, Theorem 8.9] that a $\mathrm {C}^*$
-algebras introduced in [Reference Cuntz15] and further developed in [Reference Coward, Elliott and Ivanescu14]; see also [Reference Antoine, Perera, Robert and Thiel2, Reference Antoine, Perera and Thiel3, Reference Gardella and Perera21, Reference Kirchberg and Rørdam25, Reference Rørdam43, Reference Thiel and Vilalta50, Reference Vilalta53]. Explicitly, it was shown in [Reference Thiel and Vilalta49, Theorem 8.9] that a $\mathrm {C}^*$![]() -algebra is nowhere scattered if and only if its Cuntz semigroup is weakly $(2,\,\omega )$
-algebra is nowhere scattered if and only if its Cuntz semigroup is weakly $(2,\,\omega )$![]() -divisible, a notion defined by Robert and Rørdam in [Reference Robert and Rørdam40] to study when certain $\mathrm {C}^*$
-divisible, a notion defined by Robert and Rørdam in [Reference Robert and Rørdam40] to study when certain $\mathrm {C}^*$![]() -algebras have characters; see paragraph 2.3. Consequently, the study of question 1.1 leads naturally to the study of divisibility properties of $\operatorname {Cu} (\mathcal {M}(A))$
-algebras have characters; see paragraph 2.3. Consequently, the study of question 1.1 leads naturally to the study of divisibility properties of $\operatorname {Cu} (\mathcal {M}(A))$![]() . The main divisibility properties at play in this case are weak $(2,\,\omega )$
. The main divisibility properties at play in this case are weak $(2,\,\omega )$![]() -divisibility and its bounded counterpart, known as weak $(m,\,n)$
-divisibility and its bounded counterpart, known as weak $(m,\,n)$![]() -divisibility; see paragraph 2.3 for the definitions.
-divisibility; see paragraph 2.3 for the definitions.
The nowhere scattered $\mathrm {C}^*$![]() -algebras from examples 5.2 and 5.3, which fail to have a nowhere scattered multiplier algebra, have a weakly $(2,\,\omega )$
-algebras from examples 5.2 and 5.3, which fail to have a nowhere scattered multiplier algebra, have a weakly $(2,\,\omega )$![]() -divisible Cuntz semigroup. However, they both have unbounded divisibility, that is, for every pair $m,\,n\in {\mathbb {N}}$
-divisible Cuntz semigroup. However, they both have unbounded divisibility, that is, for every pair $m,\,n\in {\mathbb {N}}$![]() there exists a Cuntz class that is not weakly $(m,\,n')$
there exists a Cuntz class that is not weakly $(m,\,n')$![]() -divisible for any $n'\leq n$
-divisible for any $n'\leq n$![]() . Thus, we ask:
. Thus, we ask:
Question 1.2 Let $A$![]() be a nowhere scattered $\mathrm {C}^*$
be a nowhere scattered $\mathrm {C}^*$![]() -algebra. When does there exist $n\in {\mathbb {N}}$
-algebra. When does there exist $n\in {\mathbb {N}}$![]() such that $[a]$
such that $[a]$![]() is weakly $(2,\,n)$
is weakly $(2,\,n)$![]() -divisible for every $a\in A_+$
-divisible for every $a\in A_+$![]() ?
?
More generally, when can one find $m,\,n\in {\mathbb {N}}$![]() such that $[a\otimes 1_m]$
such that $[a\otimes 1_m]$![]() is weakly $(2m,\,n)$
is weakly $(2m,\,n)$![]() -divisible for every $a\in A_+$
-divisible for every $a\in A_+$![]() ?
?
This question is studied in detail in § 4, where we provide a number of examples where one can answer question 1.2 affirmatively. Further, we also show that having bounded divisibility is characterized by the soft part of the monoid; see theorem 4.11.
We prove in § 5 that question 1.1 has a positive answer whenever question 1.2 does.
Theorem 1.3 5.11
Let $A$![]() be a $\sigma$
be a $\sigma$![]() -unital $\mathrm {C}^*$
-unital $\mathrm {C}^*$![]() -algebra. Assume that for every orthogonal sequence $(a_i)_i$
-algebra. Assume that for every orthogonal sequence $(a_i)_i$![]() of positive elements in $A$
of positive elements in $A$![]() there exist $m,\,n\in {\mathbb {N}}$
there exist $m,\,n\in {\mathbb {N}}$![]() such that $[a_i\otimes 1_m]$
such that $[a_i\otimes 1_m]$![]() is weakly $(2\,m,\, n)$
is weakly $(2\,m,\, n)$![]() -divisible for every $i$
-divisible for every $i$![]() . Then $\mathcal {M}(A)$
. Then $\mathcal {M}(A)$![]() is nowhere scattered.
is nowhere scattered.
Using the study of bounded divisibility from § 4, and that nowhere scatteredness passes to ideals ([Reference Thiel and Vilalta49, Proposition 4.2]), one obtains:
Theorem 1.4 5.12
Let $A$![]() be a $\sigma$
be a $\sigma$![]() -unital $\mathrm {C}^*$
-unital $\mathrm {C}^*$![]() -algebra. Assume that $A$
-algebra. Assume that $A$![]() is of
is of
(i) real rank zero, or
(ii) finite nuclear dimension, or
(iii) stable rank one with $k$
 -comparison.
-comparison.
Then $A$![]() is nowhere scattered if and only if $\mathcal {M}(A)$
is nowhere scattered if and only if $\mathcal {M}(A)$![]() is nowhere scattered.
is nowhere scattered.
Further, one can generalize (iii) above by changing stable rank one for the condition of having a surjective rank map; see proposition 4.3 and remark 4.4.
We also prove a weak converse of theorem 1.3 for stable $\mathrm {C}^*$![]() -algebras:
-algebras:
Theorem 1.5 5.18
Let $A$![]() be a $\sigma$
be a $\sigma$![]() -unital, stable $\mathrm {C}^*$
-unital, stable $\mathrm {C}^*$![]() -algebra. Assume that $\mathcal {M}(A)$
-algebra. Assume that $\mathcal {M}(A)$![]() is nowhere scattered. Then, for every $a\in A_+$
is nowhere scattered. Then, for every $a\in A_+$![]() and $m\in {\mathbb {N}}$
and $m\in {\mathbb {N}}$![]() there exists $n$
there exists $n$![]() such that $[a]$
such that $[a]$![]() is weakly $(m,\,n)$
is weakly $(m,\,n)$![]() -divisible.
-divisible.
Most of the results in § 3 and 4 can be translated to the more general setting of abstract Cuntz semigroups, or Cu-semigroups for short; see for example [Reference Antoine, Perera and Thiel3] and [Reference Gardella and Perera21]. However, since in this paper we focus on multiplier algebras (which have no known $\operatorname {Cu}$![]() -counterpart), we state all the results in the language of $\mathrm {C}^*$
-counterpart), we state all the results in the language of $\mathrm {C}^*$![]() -algebras.
-algebras.
2. Preliminaries
2.1. Nowhere scatteredness and the Global Glimm Property
As defined in [Reference Thiel and Vilalta49, Definition A], a $\mathrm {C}^*$![]() -algebra is nowhere scattered if none of its quotients contains a minimal open projection, where recall that an open projection in a $\mathrm {C}^*$
-algebra is nowhere scattered if none of its quotients contains a minimal open projection, where recall that an open projection in a $\mathrm {C}^*$![]() -algebra $B$
-algebra $B$![]() is a projection $p\in B^{**}$
is a projection $p\in B^{**}$![]() that can be written as the strong limit of an increasing sequence of positive elements in $B$
that can be written as the strong limit of an increasing sequence of positive elements in $B$![]() . As noted in [Reference Thiel and Vilalta49, Paragraph 2.1], an open projection $p\in B^{**}$
. As noted in [Reference Thiel and Vilalta49, Paragraph 2.1], an open projection $p\in B^{**}$![]() is minimal with respect to the order if and only if $p\in B$
is minimal with respect to the order if and only if $p\in B$![]() and $pBp= {\mathbb {C}} p$
and $pBp= {\mathbb {C}} p$![]() . By [Reference Thiel and Vilalta49, Theorem 3.1], a $\mathrm {C}^*$
. By [Reference Thiel and Vilalta49, Theorem 3.1], a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() is nowhere scattered if and only if no nonzero ideal-quotient of $A$
is nowhere scattered if and only if no nonzero ideal-quotient of $A$![]() is elementary.
is elementary.
One also says that a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() has the Global Glimm Property ([Reference Kirchberg and Rørdam25, Definition 4.12]) if for every $a\in A_+$
has the Global Glimm Property ([Reference Kirchberg and Rørdam25, Definition 4.12]) if for every $a\in A_+$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() there exists a ${}^*$
there exists a ${}^*$![]() -homomorphism $\varphi \colon M_2 (C_0 (0,\,1])\to \overline {aAa}$
-homomorphism $\varphi \colon M_2 (C_0 (0,\,1])\to \overline {aAa}$![]() such that the image of $\varphi$
such that the image of $\varphi$![]() contains $(a-\varepsilon )_+$
contains $(a-\varepsilon )_+$![]() .
.
A $\mathrm {C}^*$![]() -algebra is nowhere scattered whenever it has the Global Glimm Property. The converse remains open, and is known as the Global Glimm Problem; see [Reference Antoine, Perera, Robert and Thiel2], [Reference Elliott and Rørdam18] and [Reference Thiel and Vilalta51].
-algebra is nowhere scattered whenever it has the Global Glimm Property. The converse remains open, and is known as the Global Glimm Problem; see [Reference Antoine, Perera, Robert and Thiel2], [Reference Elliott and Rørdam18] and [Reference Thiel and Vilalta51].
Examples of $\mathrm {C}^*$![]() -algebras with the Global Glimm Property include simple, non-elementary $\mathrm {C}^*$
-algebras with the Global Glimm Property include simple, non-elementary $\mathrm {C}^*$![]() -algebras, $\mathcal {Z}$
-algebras, $\mathcal {Z}$![]() -stable $\mathrm {C}^*$
-stable $\mathrm {C}^*$![]() -algebras and traceless $\mathrm {C}^*$
-algebras and traceless $\mathrm {C}^*$![]() -algebras (which include purely infinite $\mathrm {C}^*$
-algebras (which include purely infinite $\mathrm {C}^*$![]() -algebras).
-algebras).
2.2. The Cuntz semigroup
For any pair of positive elements $a,\,b$![]() in a $\mathrm {C}^*$
in a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() one writes $a\precsim b$
one writes $a\precsim b$![]() if $a=\lim _n r_n b r_n^*$
if $a=\lim _n r_n b r_n^*$![]() for some sequence $(r_n)_n$
for some sequence $(r_n)_n$![]() in $A$
in $A$![]() . One also says that $a$
. One also says that $a$![]() is Cuntz equivalent to $b$
is Cuntz equivalent to $b$![]() , in symbols $a\sim b$
, in symbols $a\sim b$![]() , whenever $a\precsim b$
, whenever $a\precsim b$![]() and $b\precsim a$
and $b\precsim a$![]() .
.
The Cuntz semigroup $\operatorname {Cu} (A)$![]() is defined as the quotient $(A\otimes \mathcal {K}_+)/\!\sim$
is defined as the quotient $(A\otimes \mathcal {K}_+)/\!\sim$![]() equipped with the order induced by $\precsim$
equipped with the order induced by $\precsim$![]() and the addition induced by diagonal addition; see [Reference Cuntz15] and [Reference Coward, Elliott and Ivanescu14] for details.
and the addition induced by diagonal addition; see [Reference Cuntz15] and [Reference Coward, Elliott and Ivanescu14] for details.
Given elements $x,\,y\in \operatorname {Cu} (A)$![]() , we write $x\ll y$
, we write $x\ll y$![]() whenever there exists $a\in (A\otimes \mathcal {K})_+$
whenever there exists $a\in (A\otimes \mathcal {K})_+$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() such that $x\leq [(a-\varepsilon )_+]$
such that $x\leq [(a-\varepsilon )_+]$![]() and $y=[a]$
and $y=[a]$![]() . As shown in [Reference Coward, Elliott and Ivanescu14], every increasing sequence in $\operatorname {Cu} (A)$
. As shown in [Reference Coward, Elliott and Ivanescu14], every increasing sequence in $\operatorname {Cu} (A)$![]() has a supremum, and every element can be written as the supremum of a $\ll$
has a supremum, and every element can be written as the supremum of a $\ll$![]() -increasing sequence.
-increasing sequence.
In recent years, the Cuntz semigroup has benefited from the study of abstract Cuntz semigroups, or Cu-semigroups for short. Good references for this include [Reference Ara, Perera and Toms5], [Reference Antoine, Perera and Thiel3] and [Reference Gardella and Perera21]. In this paper, we will not use the language of Cu-semigroups (except in corollary 4.13), but we will still make use of some of the abstract properties that the Cuntz semigroup of a $\mathrm {C}^*$![]() -algebra always satisfies. These are:
-algebra always satisfies. These are:
(O5) Given $x',\,x,\,y',\,y,\,z\in \operatorname {Cu} (A)$
 such that $x+y\leq z$
such that $x+y\leq z$ with $x'\ll x$
with $x'\ll x$ and $y'\ll y$
and $y'\ll y$ , there exists $c\in \operatorname {Cu} (A)$
, there exists $c\in \operatorname {Cu} (A)$ such that $y'\ll c$
such that $y'\ll c$ and $x'+c\leq y\leq x+c$
and $x'+c\leq y\leq x+c$ .
.(O6) Given $x'\ll x\ll y+z$
 , there exist $v\leq x,\,y$
, there exist $v\leq x,\,y$ and $w\leq x,\,z$
and $w\leq x,\,z$ such that $x'\leq v+w$
such that $x'\leq v+w$ .
.
The reader is referred to [Reference Antoine, Perera and Thiel3, Proposition 4.6] (also [Reference Rørdam and Winter44]) and [Reference Robert38] for the respective proofs.
2.3. Divisibility in the Cuntz semigroup
Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra, let $x\in \operatorname {Cu} (A)$
-algebra, let $x\in \operatorname {Cu} (A)$![]() and take $n\geq 1$
and take $n\geq 1$![]() and $m\geq 2$
and $m\geq 2$![]() . Following [Reference Robert and Rørdam40], we will say that $x$
. Following [Reference Robert and Rørdam40], we will say that $x$![]() is weakly $(m,\,n)$
is weakly $(m,\,n)$![]() -divisible if, whenever $x'\ll x$
-divisible if, whenever $x'\ll x$![]() , there exist elements $y_1,\,\ldots,\,y_n$
, there exist elements $y_1,\,\ldots,\,y_n$![]() such that $x'\leq y_1+\ldots +y_n$
such that $x'\leq y_1+\ldots +y_n$![]() and $my_j\leq x$
and $my_j\leq x$![]() for each $j\leq n$
for each $j\leq n$![]() . Similarly, $x$
. Similarly, $x$![]() is weakly $(m,\,\omega )$
is weakly $(m,\,\omega )$![]() -divisible if the previous condition holds without any bound on $n$
-divisible if the previous condition holds without any bound on $n$![]() , that is, allowing $n$
, that is, allowing $n$![]() to depend on $x'$
to depend on $x'$![]() .
.
The element $x$![]() is said to be $(m,\,n)$
is said to be $(m,\,n)$![]() -divisible (resp. $(m,\,\omega )$
-divisible (resp. $(m,\,\omega )$![]() -divisible) if one can always set $y_1=\ldots =y_n$
-divisible) if one can always set $y_1=\ldots =y_n$![]() .
.
A $\mathrm {C}^*$![]() -algebra is nowhere scattered if and only if every element in its Cuntz semigroup is weakly $(m,\,\omega )$
-algebra is nowhere scattered if and only if every element in its Cuntz semigroup is weakly $(m,\,\omega )$![]() -divisible for each $m$
-divisible for each $m$![]() , whilst a $\mathrm {C}^*$
, whilst a $\mathrm {C}^*$![]() -algebra has the Global Glimm Property if and only if every element is $(m,\,\omega )$
-algebra has the Global Glimm Property if and only if every element is $(m,\,\omega )$![]() -divisible for each $m$
-divisible for each $m$![]() ; see [Reference Thiel and Vilalta49, Theorem 8.9] and [Reference Thiel and Vilalta51, Theorem 3.6] respectively.
; see [Reference Thiel and Vilalta49, Theorem 8.9] and [Reference Thiel and Vilalta51, Theorem 3.6] respectively.
3. Finite divisibility
In this section, we recall the notions of finite divisibility introduced in [Reference Robert and Rørdam40]; see definition 3.1. We prove their main properties (lemma 3.3), and study some situations where $\operatorname {Cu} (A)$![]() contains a sup-dense subset of elements with finite divisibility. We also find sufficient conditions for finite weak divisibility to imply finite divisibility; see theorem 3.15.
contains a sup-dense subset of elements with finite divisibility. We also find sufficient conditions for finite weak divisibility to imply finite divisibility; see theorem 3.15.
Definition 3.1 [Reference Robert and Rørdam40]
Let $a$![]() be a positive element of a $\mathrm {C}^*$
be a positive element of a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() , and let $m\geq 2$
, and let $m\geq 2$![]() . We let $\operatorname {div}_m ([a])$
. We let $\operatorname {div}_m ([a])$![]() and ${\rm Div}_m ([a])$
and ${\rm Div}_m ([a])$![]() be the least positive integers $n,\,n'$
be the least positive integers $n,\,n'$![]() such that $[a]\in \operatorname {Cu} (A)$
such that $[a]\in \operatorname {Cu} (A)$![]() is weakly $(m,\,n)$
is weakly $(m,\,n)$![]() -divisible and $(m,\,n')$
-divisible and $(m,\,n')$![]() -divisible respectively.
-divisible respectively.
If no such $n$![]() or $n'$
or $n'$![]() exist, we set $\operatorname {div}_m ([a])=\infty$
exist, we set $\operatorname {div}_m ([a])=\infty$![]() or ${\rm Div}_m ([a])=\infty$
or ${\rm Div}_m ([a])=\infty$![]() .
.
Remark 3.2 The class of a positive element $a\in A_+$![]() in $\operatorname {Cu} (A)$
in $\operatorname {Cu} (A)$![]() is said to be compact if $[a]\ll [a]$
is said to be compact if $[a]\ll [a]$![]() . Every projection gives rise to a compact Cuntz class and, in some cases, these are the only compact classes; see [Reference Brown and Ciuperca10].
. Every projection gives rise to a compact Cuntz class and, in some cases, these are the only compact classes; see [Reference Brown and Ciuperca10].
Given a compact element $[a]\in \operatorname {Cu} (A)$![]() , then $[a]$
, then $[a]$![]() is weakly $(m,\,\omega )$
is weakly $(m,\,\omega )$![]() -divisible if and only if $\operatorname {div}_m ([a])<\infty$
-divisible if and only if $\operatorname {div}_m ([a])<\infty$![]() .
.
However, for a non-compact element $[a]$![]() , $\operatorname {div}_m ([a])<\infty$
, $\operatorname {div}_m ([a])<\infty$![]() is not equivalent to $[a]$
is not equivalent to $[a]$![]() being weakly $(m,\,\omega )$
being weakly $(m,\,\omega )$![]() -divisible; see example 3.6 and remark 5.10.
-divisible; see example 3.6 and remark 5.10.
Let us first summarize the main properties of $\operatorname {div}_m ()$![]() . Part (iii) of the following lemma is in analogy to [Reference Kirchberg and Rørdam25, Lemma 4.9], while (iv) is a $\operatorname {Cu}$
. Part (iii) of the following lemma is in analogy to [Reference Kirchberg and Rørdam25, Lemma 4.9], while (iv) is a $\operatorname {Cu}$![]() -analogue of [Reference Robert and Rørdam40, Proposition 3.6].
-analogue of [Reference Robert and Rørdam40, Proposition 3.6].
Recall that, given $x,\,y\in \operatorname {Cu} (A)$![]() , the infimum $x\wedge \infty y$
, the infimum $x\wedge \infty y$![]() always exists; see [Reference Antoine, Perera, Robert and Thiel1, Remark 2.6]. Here, $\infty y$
always exists; see [Reference Antoine, Perera, Robert and Thiel1, Remark 2.6]. Here, $\infty y$![]() denotes the element $\sup _n ny$
denotes the element $\sup _n ny$![]() .
.
Lemma 3.3 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra, and let $x=[a]\in \operatorname {Cu} (A)$
-algebra, and let $x=[a]\in \operatorname {Cu} (A)$![]() and $m\in {\mathbb {N}}$
and $m\in {\mathbb {N}}$![]() . Then,
. Then,
(i) $\operatorname {div}_m (x)\leq \operatorname {div}_{m'} (x)$
 whenever $m\leq m'$
whenever $m\leq m'$ .
.(ii) $\operatorname {div}_m ([a])\leq N(\operatorname {div}_m ([b_1]) +\ldots + \operatorname {div}_m ([b_r]))$
 whenever
\[ [b_1],\ldots ,[b_r]\leq [a]\leq N([b_1]+\ldots +[b_r]). \]
whenever
\[ [b_1],\ldots ,[b_r]\leq [a]\leq N([b_1]+\ldots +[b_r]). \]
(iii) $\operatorname {div}_m ([a+b])\leq \operatorname {div}_m ([a]) + \operatorname {div}_m ([b])$
 .
.(iv) Given $x,\,y\in \operatorname {Cu} (A)$
 such that $y\leq x$
such that $y\leq x$ and $x\wedge \infty y=y$
and $x\wedge \infty y=y$ , then $\operatorname {div}_m (y)\leq \operatorname {div}_m (x)$
, then $\operatorname {div}_m (y)\leq \operatorname {div}_m (x)$ .
.(v) $\operatorname {div}_m (x)\leq \sup _k \operatorname {div}_m (x_k)$
 for every increasing sequence $(x_k)_k$
for every increasing sequence $(x_k)_k$ in $\operatorname {Cu} (A)$
in $\operatorname {Cu} (A)$ with supremum $x$
with supremum $x$ .
.
Proof. (i) follows directly from the definition of $\operatorname {div}_m ([a])$![]() .
.
To see (ii), let $n_j=\operatorname {div}_m ([b_j])$![]() for $j=1,\,\ldots,\,r$
for $j=1,\,\ldots,\,r$![]() . We may assume that all quantities are finite, since otherwise we are done.
. We may assume that all quantities are finite, since otherwise we are done.
Take $x\ll [a]$![]() . Since $[a]\leq N[b_1]+\ldots +N[b_r]$
. Since $[a]\leq N[b_1]+\ldots +N[b_r]$![]() , we can find elements $x_j$
, we can find elements $x_j$![]() such that $x_j\ll [b_j]$
such that $x_j\ll [b_j]$![]() and $x\leq Nx_1+\ldots +Nx_r$
and $x\leq Nx_1+\ldots +Nx_r$![]() . The element $[b_j]$
. The element $[b_j]$![]() is weakly $(m,\,n_j)$
is weakly $(m,\,n_j)$![]() -divisible, so we can find elements $y_{1,j},\,\ldots,\,y_{n_j,j}$
-divisible, so we can find elements $y_{1,j},\,\ldots,\,y_{n_j,j}$![]() such that
such that
for each $i$![]() and $j$
and $j$![]() .
.
Using that $[b_j]\leq [a]$![]() , one has $my_{i,j}\leq [a]$
, one has $my_{i,j}\leq [a]$![]() . Further, since we also have $x\leq N\sum _j x_j$
. Further, since we also have $x\leq N\sum _j x_j$![]() , we deduce that $x\leq N\sum _{i,j} y_{i,j}$
, we deduce that $x\leq N\sum _{i,j} y_{i,j}$![]() . It follows that $\operatorname {Div}_m ([a])\leq N(n_1+\ldots +n_r)$
. It follows that $\operatorname {Div}_m ([a])\leq N(n_1+\ldots +n_r)$![]() , as desired.
, as desired.
Note that, given $a,\,b\in (A\otimes \mathcal {K})_+$![]() , we have $[a+b]\leq [a]+[b]$
, we have $[a+b]\leq [a]+[b]$![]() and $[a],\,[b]\leq [a+b]$
and $[a],\,[b]\leq [a+b]$![]() . Thus, (iii) follows directly from (ii).
. Thus, (iii) follows directly from (ii).
For (iv), let $x,\,y\in \operatorname {Cu} (A)$![]() be as stated. As before, we may assume that $\operatorname {div}_m (x)=n$
be as stated. As before, we may assume that $\operatorname {div}_m (x)=n$![]() for some $n\in {\mathbb {N}}$
for some $n\in {\mathbb {N}}$![]() . Take $y'\ll y$
. Take $y'\ll y$![]() , and apply the weak $(m,\,n)$
, and apply the weak $(m,\,n)$![]() -divisibility of $x$
-divisibility of $x$![]() to obtain elements $y_1,\,\ldots,\,y_n$
to obtain elements $y_1,\,\ldots,\,y_n$![]() satisfying the properties from paragraph 2.3 for $y'$
satisfying the properties from paragraph 2.3 for $y'$![]() and $x$
and $x$![]() .
.
Since $my_j\leq x$![]() for every $j$
for every $j$![]() , and $x\wedge \infty y=y$
, and $x\wedge \infty y=y$![]() , one obtains $m(y_j\wedge \infty y)\leq x\wedge \infty y=y$
, one obtains $m(y_j\wedge \infty y)\leq x\wedge \infty y=y$![]() . To see that $y'\leq (y_1\wedge \infty y)+\ldots +(y_n\wedge \infty y)$
. To see that $y'\leq (y_1\wedge \infty y)+\ldots +(y_n\wedge \infty y)$![]() , note that $y'$
, note that $y'$![]() is bounded by $y$
is bounded by $y$![]() (and thus $\infty y$
(and thus $\infty y$![]() ) and by $y_1+\ldots +y_n$
) and by $y_1+\ldots +y_n$![]() . Using that the map $t\mapsto t\wedge \infty y$
. Using that the map $t\mapsto t\wedge \infty y$![]() preserves addition [Reference Antoine, Perera, Robert and Thiel1, Theorem 2.5(i)], one has
preserves addition [Reference Antoine, Perera, Robert and Thiel1, Theorem 2.5(i)], one has
which shows that the elements $y_j\wedge \infty y$![]() satisfy the conditions from paragraph 2.3 for $y'$
satisfy the conditions from paragraph 2.3 for $y'$![]() and $y$
and $y$![]() , as required.
, as required.
To prove (v), assume that the supremum $\sup _k \operatorname {div}_m (x_k)$![]() is finite, since otherwise there is nothing to prove. Let $n\in {\mathbb {N}}$
is finite, since otherwise there is nothing to prove. Let $n\in {\mathbb {N}}$![]() be such that $\sup _k \operatorname {div}_m (x_k)\leq n$
be such that $\sup _k \operatorname {div}_m (x_k)\leq n$![]() , and take $x'\in \operatorname {Cu} (A)$
, and take $x'\in \operatorname {Cu} (A)$![]() such that $x'\ll x$
such that $x'\ll x$![]() . Since $x=\sup _k x_k$
. Since $x=\sup _k x_k$![]() , it follows that $x'\ll x_k$
, it follows that $x'\ll x_k$![]() for some $k\in {\mathbb {N}}$
for some $k\in {\mathbb {N}}$![]() . Thus, using that $\operatorname {div}_m (x_k)\leq n$
. Thus, using that $\operatorname {div}_m (x_k)\leq n$![]() , we obtain elements $y_1,\,\ldots,\,y_n$
, we obtain elements $y_1,\,\ldots,\,y_n$![]() with $x'\leq y_1+\ldots +y_n$
with $x'\leq y_1+\ldots +y_n$![]() and $my_j\leq x_k\leq x$
and $my_j\leq x_k\leq x$![]() for each $j$
for each $j$![]() . We get that $\operatorname {div}_m (x)\leq n$
. We get that $\operatorname {div}_m (x)\leq n$![]() , as desired.
, as desired.
Recall that a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() is said to have strict comparison if $[a]\leq [b]$
is said to have strict comparison if $[a]\leq [b]$![]() in $\operatorname {Cu} (A)$
in $\operatorname {Cu} (A)$![]() whenever there exists $\delta >0$
whenever there exists $\delta >0$![]() such that $\lim _n \tau (a^{1/n})\leq (1-\delta )\lim _n \tau (b^{1/n})$
such that $\lim _n \tau (a^{1/n})\leq (1-\delta )\lim _n \tau (b^{1/n})$![]() for every $2$
for every $2$![]() -quasitrace $\tau$
-quasitrace $\tau$![]() ; see [Reference Elliott, Robert and Santiago17] for more details.
; see [Reference Elliott, Robert and Santiago17] for more details.
Lemma 3.4 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra, let $[a]\in \operatorname {Cu} (A)$
-algebra, let $[a]\in \operatorname {Cu} (A)$![]() and $m\in {\mathbb {N}}$
and $m\in {\mathbb {N}}$![]() . Then,
. Then,
for every $k\in {\mathbb {N}}$![]() .
.
If $A$![]() has strict comparison, one has $\operatorname {div}_{m} ([a])\leq \operatorname {div}_{k(m+1)}(k[a])$
has strict comparison, one has $\operatorname {div}_{m} ([a])\leq \operatorname {div}_{k(m+1)}(k[a])$![]() .
.
Proof. Let $n=\operatorname {div}_m ([a])$![]() , which we may assume to be finite, and take $x\ll k[a]$
, which we may assume to be finite, and take $x\ll k[a]$![]() . Then, there exists $\varepsilon >0$
. Then, there exists $\varepsilon >0$![]() such that $x\ll k[(a-\varepsilon )_+]$
such that $x\ll k[(a-\varepsilon )_+]$![]() . Since $[(a-\varepsilon )_+]\ll [a]$
. Since $[(a-\varepsilon )_+]\ll [a]$![]() , there exist $y_1,\,\ldots,\,y_n\in \operatorname {Cu} (A)$
, there exist $y_1,\,\ldots,\,y_n\in \operatorname {Cu} (A)$![]() such that
such that
for each $j$![]() .
.
In particular, one gets
which implies $\operatorname {div}_{km}(k[a])\leq n$![]() , as desired.
, as desired.
Now assume that $A$![]() has strict comparison of positive elements, and let $n=\operatorname {div}_{k(m+1)}(k[a])$
has strict comparison of positive elements, and let $n=\operatorname {div}_{k(m+1)}(k[a])$![]() . As before, we may assume $n$
. As before, we may assume $n$![]() to be finite. Let $x\ll [a]$
to be finite. Let $x\ll [a]$![]() , which implies $kx\ll k[a]$
, which implies $kx\ll k[a]$![]() . Then, there exist $z_1,\,\ldots,\,z_n$
. Then, there exist $z_1,\,\ldots,\,z_n$![]() such that $x\leq kx\leq z_1+\ldots +z_n$
such that $x\leq kx\leq z_1+\ldots +z_n$![]() and $k(m+1)z_j\leq k[a]$
and $k(m+1)z_j\leq k[a]$![]() . Thus, one has $(km+1)mz_j\leq km(m+1)z_j\leq (km)[a]$
. Thus, one has $(km+1)mz_j\leq km(m+1)z_j\leq (km)[a]$![]() .
.
Using [Reference Elliott, Robert and Santiago17, Proposition 6.2], we get $mz_j\leq [a]$![]() . This implies $\operatorname {div}_{m} ([a])\leq \operatorname {div}_{k(m+1)}(k[a])$
. This implies $\operatorname {div}_{m} ([a])\leq \operatorname {div}_{k(m+1)}(k[a])$![]() .
.
Remark 3.5 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra and let $m\in {\mathbb {N}}$
-algebra and let $m\in {\mathbb {N}}$![]() . Assume that $\operatorname {div}_{m} ([a])<\infty$
. Assume that $\operatorname {div}_{m} ([a])<\infty$![]() for every $a\in A_+$
for every $a\in A_+$![]() . Lemma 3.3 (ii) implies, in particular, that $\operatorname {div}_m ( [b] )<\infty$
. Lemma 3.3 (ii) implies, in particular, that $\operatorname {div}_m ( [b] )<\infty$![]() for every $b\in M_n (A)_+$
for every $b\in M_n (A)_+$![]() and $n\in {\mathbb {N}}$
and $n\in {\mathbb {N}}$![]() .
.
Indeed, given $b\in M_n(A)_+$![]() there exist elements $b_1,\,\ldots,\, b_n\in A_+$
there exist elements $b_1,\,\ldots,\, b_n\in A_+$![]() and $N\in {\mathbb {N}}$
and $N\in {\mathbb {N}}$![]() such that $[b_i]\leq [b]\leq N([b_1]+\ldots +[b_n])$
such that $[b_i]\leq [b]\leq N([b_1]+\ldots +[b_n])$![]() for each $i\leq n$
for each $i\leq n$![]() ; see [Reference Antoine, Perera and Thiel4, 4.2] and [Reference Thiel and Vilalta51, Lemma 3.3].
; see [Reference Antoine, Perera and Thiel4, 4.2] and [Reference Thiel and Vilalta51, Lemma 3.3].
By lemma 3.3 (ii), we have that $\operatorname {div}_{m} (b)<\infty$![]() , as desired.
, as desired.
Example 3.6 Let $(A_k)_k$![]() be a family of unital $\mathrm {C}^*$
be a family of unital $\mathrm {C}^*$![]() -algebras such that
-algebras such that
for each $k$![]() .
.
By [Reference Robert and Rørdam40, Theorem 7.9], such $\mathrm {C}^*$![]() -algebras can be taken to be simple, unital, infinite dimensional AH-algebras. Using [Reference Thiel and Vilalta49, Proposition 4.13], one sees that $A:=\oplus _k A_k$
-algebras can be taken to be simple, unital, infinite dimensional AH-algebras. Using [Reference Thiel and Vilalta49, Proposition 4.13], one sees that $A:=\oplus _k A_k$![]() is nowhere scattered. Thus, every element in $\operatorname {Cu} (A)$
is nowhere scattered. Thus, every element in $\operatorname {Cu} (A)$![]() is weakly $(2,\,\omega )$
is weakly $(2,\,\omega )$![]() -divisible.
-divisible.
Consider the element $x=\sup _n \sum _{k=1}^n [1_{A_k}]\in \operatorname {Cu} (\oplus _k A_k)$![]() , and denote by $\iota _k$
, and denote by $\iota _k$![]() the induced inclusion $\operatorname {Cu} (A_k)\to \operatorname {Cu} (\oplus _k A_k)$
the induced inclusion $\operatorname {Cu} (A_k)\to \operatorname {Cu} (\oplus _k A_k)$![]() . Then,
. Then,
Thus, lemma 3.3 (iv) implies that
This shows that $x$![]() is weakly $(2,\,\omega )$
is weakly $(2,\,\omega )$![]() -divisible, but $\operatorname {div}_2 (x)=\infty$
-divisible, but $\operatorname {div}_2 (x)=\infty$![]() ; see also corollary 5.16.
; see also corollary 5.16.
We now move our attention to $\mathrm {C}^*$![]() -algebras whose Cuntz semigroup $\operatorname {Cu} (A)$
-algebras whose Cuntz semigroup $\operatorname {Cu} (A)$![]() satisfies that every element (or, at least, a finite multiple of it) has finite weak divisibility. Particularly, there will be some situations where we do not know if an element $a\in A_+$
satisfies that every element (or, at least, a finite multiple of it) has finite weak divisibility. Particularly, there will be some situations where we do not know if an element $a\in A_+$![]() satisfies $\operatorname {div}_2 ([a])<\infty$
satisfies $\operatorname {div}_2 ([a])<\infty$![]() , but where we do know that $\operatorname {div}_{2m} ([a\otimes 1_m])<\infty$
, but where we do know that $\operatorname {div}_{2m} ([a\otimes 1_m])<\infty$![]() for some $m\in {\mathbb {N}}$
for some $m\in {\mathbb {N}}$![]() . This is the case, for example, when $a$
. This is the case, for example, when $a$![]() is a positive element in a nowhere scattered $\mathrm {C}^*$
is a positive element in a nowhere scattered $\mathrm {C}^*$![]() -algebra of finite nuclear dimension (see proposition 4.1). Keeping track of such elements will be important in our investigations, and so we provide a precise definition for them:
-algebra of finite nuclear dimension (see proposition 4.1). Keeping track of such elements will be important in our investigations, and so we provide a precise definition for them:
Definition 3.7 Let A be a $\mathrm {C}^*$![]() -algebra, and let $[a]\in \operatorname {Cu} (A)$
-algebra, and let $[a]\in \operatorname {Cu} (A)$![]() . We will say that
. We will say that
(i) $[a]$
 is of finite weak divisibility if ${\rm div}_{2m}([a])<\infty$
is of finite weak divisibility if ${\rm div}_{2m}([a])<\infty$ for some $m\in {\mathbb {N}}$
for some $m\in {\mathbb {N}}$ .
.(ii) $[a]$
 has a multiple of finite weak divisibility if ${\rm div}_{2m}(m[a])<\infty$
has a multiple of finite weak divisibility if ${\rm div}_{2m}(m[a])<\infty$ for some ${m\in {\mathbb {N}}}$
for some ${m\in {\mathbb {N}}}$ .
.(iii) $[a]$
 has a multiple of finite divisibility if ${\rm Div}_{2m}(m[a])<\infty$
has a multiple of finite divisibility if ${\rm Div}_{2m}(m[a])<\infty$ for some $m\in {\mathbb {N}}$
for some $m\in {\mathbb {N}}$ .
.
We will denote by $\operatorname {Cu} (A)_{\operatorname {div}}$![]() (resp. $\operatorname {Cu} (A)_{\operatorname {mdiv}}$
(resp. $\operatorname {Cu} (A)_{\operatorname {mdiv}}$![]() and $\operatorname {Cu} (A)_{\rm mDiv}$
and $\operatorname {Cu} (A)_{\rm mDiv}$![]() ) the subset of $\operatorname {Cu} (A)$
) the subset of $\operatorname {Cu} (A)$![]() consisting of the elements $[a]$
consisting of the elements $[a]$![]() of finite weak divisibility (resp. with a multiple of finite weak divisibility, and with a multiple of finite divisibility).
of finite weak divisibility (resp. with a multiple of finite weak divisibility, and with a multiple of finite divisibility).
Remark 3.8 Note that one always has $\operatorname {Cu} (A)_{\operatorname {div}}\subseteq \operatorname {Cu} (A)_{\operatorname {mdiv}}$![]() . Further, $\operatorname {Cu} (A)_{\operatorname {div}}$
. Further, $\operatorname {Cu} (A)_{\operatorname {div}}$![]() and $\operatorname {Cu} (A)_{\operatorname {mdiv}}$
and $\operatorname {Cu} (A)_{\operatorname {mdiv}}$![]() agree whenever $\operatorname {Cu} (A)$
agree whenever $\operatorname {Cu} (A)$![]() is unperforated. Indeed, let $[a]\in \operatorname {Cu} (A)$
is unperforated. Indeed, let $[a]\in \operatorname {Cu} (A)$![]() and $m\in {\mathbb {N}}$
and $m\in {\mathbb {N}}$![]() be such that $\operatorname {div}_{2m} (m[a])=n<\infty$
be such that $\operatorname {div}_{2m} (m[a])=n<\infty$![]() . For any $\varepsilon >0$
. For any $\varepsilon >0$![]() , we have $m[(a-\varepsilon )_+]\ll m[a]$
, we have $m[(a-\varepsilon )_+]\ll m[a]$![]() . Thus, there exist $y_1,\,\ldots,\,y_n\in \operatorname {Cu} (A)$
. Thus, there exist $y_1,\,\ldots,\,y_n\in \operatorname {Cu} (A)$![]() such that
such that
Since $\operatorname {Cu} (A)$![]() is unperforated, we get $2y_j\leq [a]$
is unperforated, we get $2y_j\leq [a]$![]() . This shows that $\operatorname {div}_{2} ([a])\leq n<\infty$
. This shows that $\operatorname {div}_{2} ([a])\leq n<\infty$![]() , as desired.
, as desired.
Example 3.9 If $A= {\mathbb {C}}$![]() , its Cuntz semigroup is isomorphic to $\overline {{\mathbb {N}}}:={\mathbb {N}}\cup \{\infty \}$
, its Cuntz semigroup is isomorphic to $\overline {{\mathbb {N}}}:={\mathbb {N}}\cup \{\infty \}$![]() . It is readily checked that $\operatorname {div}_m (x)<\infty$
. It is readily checked that $\operatorname {div}_m (x)<\infty$![]() if and only if $x\geq m$
if and only if $x\geq m$![]() . Thus, one has $\operatorname {Cu} (A)_{\operatorname {div}} = \operatorname {Cu} (A)_{\operatorname {mdiv}} = \{ 0,\,2,\,3,\, \ldots,\, \infty \}$
. Thus, one has $\operatorname {Cu} (A)_{\operatorname {div}} = \operatorname {Cu} (A)_{\operatorname {mdiv}} = \{ 0,\,2,\,3,\, \ldots,\, \infty \}$![]() .
.
Example 3.10 Every $\mathcal {Z}$![]() -stable $\mathrm {C}^*$
-stable $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() satisfies $\operatorname {Cu} (A)=\operatorname {Cu} (A)_{\operatorname {div}}$
satisfies $\operatorname {Cu} (A)=\operatorname {Cu} (A)_{\operatorname {div}}$![]() by [Reference Winter54, Proposition 3.7]. More generally, recall that a $\mathrm {C}^*$
by [Reference Winter54, Proposition 3.7]. More generally, recall that a $\mathrm {C}^*$![]() -algebra is said to be $N$
-algebra is said to be $N$![]() -almost divisible (see [Reference Winter54]) if for each pair $x',\,x\in \operatorname {Cu} (A)$
-almost divisible (see [Reference Winter54]) if for each pair $x',\,x\in \operatorname {Cu} (A)$![]() satisfying $x'\ll x$
satisfying $x'\ll x$![]() , and $k\in {\mathbb {N}}$
, and $k\in {\mathbb {N}}$![]() , there exists $y\in \operatorname {Cu} (A)$
, there exists $y\in \operatorname {Cu} (A)$![]() such that
such that
Thus, if $A$![]() is $N$
is $N$![]() -almost divisible for some $N\in {\mathbb {N}}$
-almost divisible for some $N\in {\mathbb {N}}$![]() , one also has $\operatorname {Cu} (A)=\operatorname {Cu} (A)_{\operatorname {div} }$
, one also has $\operatorname {Cu} (A)=\operatorname {Cu} (A)_{\operatorname {div} }$![]() .
.
By [Reference Robert and Tikuisis41, Theorem 3.1], every nowhere scattered $\mathrm {C}^*$![]() -algebra of nuclear dimension $N$
-algebra of nuclear dimension $N$![]() that has no nonzero, simple, purely infinite ideal-quotients is $N$
that has no nonzero, simple, purely infinite ideal-quotients is $N$![]() -almost divisible. This includes residually stably finite, nowhere scattered $\mathrm {C}^*$
-almost divisible. This includes residually stably finite, nowhere scattered $\mathrm {C}^*$![]() -algebras of finite nuclear dimension, and nowhere scattered $\mathrm {C}^*$
-algebras of finite nuclear dimension, and nowhere scattered $\mathrm {C}^*$![]() -algebras of finite decomposition rank. Consequently, one has $\operatorname {Cu} (A)_{\operatorname {div}}=\operatorname {Cu} (A)$
-algebras of finite decomposition rank. Consequently, one has $\operatorname {Cu} (A)_{\operatorname {div}}=\operatorname {Cu} (A)$![]() .
.
As we will see in proposition 4.1, $\operatorname {Cu} (A)_{\operatorname {mdiv}}=\operatorname {Cu} (A)$![]() for any nowhere scattered $\mathrm {C}^*$
for any nowhere scattered $\mathrm {C}^*$![]() -algebra of finite nuclear dimension. In fact, one has more: $\operatorname {Cu} (\oplus _{i=1}^\infty A)_{\rm mDiv} = \operatorname {Cu} (\oplus _{i=1}^\infty A)$
-algebra of finite nuclear dimension. In fact, one has more: $\operatorname {Cu} (\oplus _{i=1}^\infty A)_{\rm mDiv} = \operatorname {Cu} (\oplus _{i=1}^\infty A)$![]() .
.
Example 3.11 As shown in [Reference Thiel and Vilalta49, Theorem 9.1], every element $x$![]() in the Cuntz semigroup of a nowhere scattered, real rank zero $\mathrm {C}^*$
in the Cuntz semigroup of a nowhere scattered, real rank zero $\mathrm {C}^*$![]() -algebra is weakly divisible, that is, there exist $y,\,z$
-algebra is weakly divisible, that is, there exist $y,\,z$![]() such that $x=2y+3z$
such that $x=2y+3z$![]() . In particular, one gets
. In particular, one gets
Thus, it follows that $\operatorname {div}_2(x)\leq 3$![]() for every $x$
for every $x$![]() and, consequently, that $\operatorname {Cu} (A)_{\operatorname {div}} = \operatorname {Cu} (A)$
and, consequently, that $\operatorname {Cu} (A)_{\operatorname {div}} = \operatorname {Cu} (A)$![]() .
.
As noted in example 3.11 above, every element in the Cuntz semigroup of a nowhere scattered, real rank zero $\mathrm {C}^*$![]() -algebra has finite divisibility. Lemmas 3.12 and 3.14 below show that the same is true for a sup-dense subset of (non-elementary) simple $\mathrm {C}^*$
-algebra has finite divisibility. Lemmas 3.12 and 3.14 below show that the same is true for a sup-dense subset of (non-elementary) simple $\mathrm {C}^*$![]() -algebras and nowhere scattered $\mathrm {C}^*$
-algebras and nowhere scattered $\mathrm {C}^*$![]() -algebras of topological dimension zero. However, this may not imply that every element in such a $\mathrm {C}^*$
-algebras of topological dimension zero. However, this may not imply that every element in such a $\mathrm {C}^*$![]() -algebra has finite weak divisibility.
-algebra has finite weak divisibility.
Recall that an element $x\in \operatorname {Cu} (A)$![]() is idempotent if $x=2x$
is idempotent if $x=2x$![]() . In the Cuntz semigroup of a simple $\mathrm {C}^*$
. In the Cuntz semigroup of a simple $\mathrm {C}^*$![]() -algebra there is only one nonzero idempotent element, which we denote by $\infty$
-algebra there is only one nonzero idempotent element, which we denote by $\infty$![]() .
.
Lemma 3.12 Let $A$![]() be a simple, non-elementary $\mathrm {C}^*$
be a simple, non-elementary $\mathrm {C}^*$![]() -algebra. Then, $\operatorname {Cu} (A)_{\operatorname {div}}$
-algebra. Then, $\operatorname {Cu} (A)_{\operatorname {div}}$![]() is sup-dense in $\operatorname {Cu} (A)$
is sup-dense in $\operatorname {Cu} (A)$![]() .
.
If $A$![]() is not stably finite, then $\operatorname {Cu} (A)_{\operatorname {div}}=\operatorname {Cu} (A)$
is not stably finite, then $\operatorname {Cu} (A)_{\operatorname {div}}=\operatorname {Cu} (A)$![]() .
.
Proof. Let $m\in {\mathbb {N}}$![]() . If $A$
. If $A$![]() is simple and non-elementary, it follows from [Reference Robert38, Proposition 5.2.1] that $\operatorname {Cu} (A)$
is simple and non-elementary, it follows from [Reference Robert38, Proposition 5.2.1] that $\operatorname {Cu} (A)$![]() is $(m,\,\omega )$
is $(m,\,\omega )$![]() -divisible.
-divisible.
Let $x\in \operatorname {Cu} (A)$![]() be such that $x\ll \infty$
be such that $x\ll \infty$![]() . Then, using that $x$
. Then, using that $x$![]() is $(m,\,\omega )$
is $(m,\,\omega )$![]() -divisible, there exists a nonzero element $y\in \operatorname {Cu} (A)$
-divisible, there exists a nonzero element $y\in \operatorname {Cu} (A)$![]() such that $my\leq x$
such that $my\leq x$![]() . Using that $x\ll \infty = \infty y$
. Using that $x\ll \infty = \infty y$![]() , we find $n\in {\mathbb {N}}$
, we find $n\in {\mathbb {N}}$![]() such that $x\leq ny$
such that $x\leq ny$![]() . This implies that $\operatorname {div}_m (x)\leq n$
. This implies that $\operatorname {div}_m (x)\leq n$![]() . Since the subset of elements compactly contained in $\infty$
. Since the subset of elements compactly contained in $\infty$![]() is sup-dense in $\operatorname {Cu} (A)$
is sup-dense in $\operatorname {Cu} (A)$![]() , the result follows.
, the result follows.
Now assume that $A$![]() is not stably finite. Then, the element $\infty$
is not stably finite. Then, the element $\infty$![]() in $\operatorname {Cu} (A)$
in $\operatorname {Cu} (A)$![]() is compact; see, for example, [Reference Thiel46, Lemma 6.21] or the proof of [Reference Bosa7, Theorem 2.6].
is compact; see, for example, [Reference Thiel46, Lemma 6.21] or the proof of [Reference Bosa7, Theorem 2.6].
It follows that every element in $\operatorname {Cu} (A)$![]() is compactly contained in $\infty$
is compactly contained in $\infty$![]() . Using the argument above, we see that $\operatorname {Cu} (A)_{\operatorname {div}}=\operatorname {Cu} (A)$
. Using the argument above, we see that $\operatorname {Cu} (A)_{\operatorname {div}}=\operatorname {Cu} (A)$![]() .
.
Remark 3.13 An inspection of the proof shows that lemma 3.12 is slightly more general: For a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() , one has $\operatorname {Cu} (A)_{\operatorname {div}}=\operatorname {Cu} (A)$
, one has $\operatorname {Cu} (A)_{\operatorname {div}}=\operatorname {Cu} (A)$![]() whenever every idempotent element in $\operatorname {Cu} (A)$
whenever every idempotent element in $\operatorname {Cu} (A)$![]() is compact.
is compact.
As defined in [Reference Brown and Pedersen9, Remark 2.5 (vi)], a $\mathrm {C}^*$![]() -algebra has topological dimension zero whenever its primitive ideal space has a basis of compact-open subsets. Examples include all $\mathrm {C}^*$
-algebra has topological dimension zero whenever its primitive ideal space has a basis of compact-open subsets. Examples include all $\mathrm {C}^*$![]() -algebras with the ideal property.
-algebras with the ideal property.
Lemma 3.14 Let $A$![]() be a separable nowhere scattered $\mathrm {C}^*$
be a separable nowhere scattered $\mathrm {C}^*$![]() -algebra of topological dimension zero. Then $\operatorname {Cu} (A)_{\operatorname {div}}$
-algebra of topological dimension zero. Then $\operatorname {Cu} (A)_{\operatorname {div}}$![]() is dense in $\operatorname {Cu} (A)$
is dense in $\operatorname {Cu} (A)$![]() .
.
Proof. Take $y\in \operatorname {Cu} (A)$![]() , and assume that there exists $y'\in \operatorname {Cu} (A)$
, and assume that there exists $y'\in \operatorname {Cu} (A)$![]() such that $y'\ll y\ll \infty y'$
such that $y'\ll y\ll \infty y'$![]() . Let $M\in {\mathbb {N}}$
. Let $M\in {\mathbb {N}}$![]() be such that $y\leq My'$
be such that $y\leq My'$![]() . Using that $y$
. Using that $y$![]() is weakly $(m,\,\omega )$
is weakly $(m,\,\omega )$![]() -divisible, one finds $y_1,\,\ldots,\, y_n$
-divisible, one finds $y_1,\,\ldots,\, y_n$![]() such that $my_i\leq y$
such that $my_i\leq y$![]() and $y'\leq y_1+\ldots y_n$
and $y'\leq y_1+\ldots y_n$![]() . Thus, one has $y\leq My_1+\ldots +My_n$
. Thus, one has $y\leq My_1+\ldots +My_n$![]() , and we get $\operatorname {div}_m (y)\leq Mn$
, and we get $\operatorname {div}_m (y)\leq Mn$![]() .
.
Since $A$![]() is separable and of topological dimension zero, it follows from [Reference Thiel and Vilalta51, Proposition 4.18] that the Cu-semigroup $\operatorname {Cu} (A)\otimes \{ 0,\,\infty \}$
is separable and of topological dimension zero, it follows from [Reference Thiel and Vilalta51, Proposition 4.18] that the Cu-semigroup $\operatorname {Cu} (A)\otimes \{ 0,\,\infty \}$![]() is algebraic. Thus, we know from [Reference Thiel and Vilalta51, Lemma 4.16] that for every pair $x',\,x\in \operatorname {Cu} (A)$
is algebraic. Thus, we know from [Reference Thiel and Vilalta51, Lemma 4.16] that for every pair $x',\,x\in \operatorname {Cu} (A)$![]() such that $x'\ll x$
such that $x'\ll x$![]() there exist $y',\,y\in \operatorname {Cu} (A)$
there exist $y',\,y\in \operatorname {Cu} (A)$![]() satisfying $x'\ll y\ll x$
satisfying $x'\ll y\ll x$![]() and $y'\ll y\ll \infty y'$
and $y'\ll y\ll \infty y'$![]() . The first part of the proof shows that $\operatorname {div}_m (y)<\infty$
. The first part of the proof shows that $\operatorname {div}_m (y)<\infty$![]() and, consequently, that $\operatorname {Cu} (A)_{\operatorname {div}}$
and, consequently, that $\operatorname {Cu} (A)_{\operatorname {div}}$![]() is dense in $\operatorname {Cu} (A)$
is dense in $\operatorname {Cu} (A)$![]() .
.
3.1 The Global Glimm Problem
We finish this section by studying when $\operatorname {Cu} (A)_{\rm div}=\operatorname {Cu} (A)$![]() implies $\operatorname {Cu} (A)_{\rm Div}=\operatorname {Cu} (A)$
implies $\operatorname {Cu} (A)_{\rm Div}=\operatorname {Cu} (A)$![]() . More concretely, we study when an element of finite weak divisibility has finite divisibility. Given its similarities with the Global Glimm Problem (see Paragraph 2.1), one could call this the discrete Global Glimm Problem.
. More concretely, we study when an element of finite weak divisibility has finite divisibility. Given its similarities with the Global Glimm Problem (see Paragraph 2.1), one could call this the discrete Global Glimm Problem.
Following the ideas from [Reference Thiel and Vilalta51, Section 6], we obtain:
Theorem 3.15 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra satisfying $\operatorname {Cu} (A)_{\rm div}=\operatorname {Cu} (A)$
-algebra satisfying $\operatorname {Cu} (A)_{\rm div}=\operatorname {Cu} (A)$![]() . Assume that there exist $k\in {\mathbb {N}}$
. Assume that there exist $k\in {\mathbb {N}}$![]() and maps $N,\,M\colon {\mathbb {N}}\to {\mathbb {N}}$
and maps $N,\,M\colon {\mathbb {N}}\to {\mathbb {N}}$![]() such that
such that
(i) whenever $x'\ll x\leq ny,\,nz$
 , there exists $t\in \operatorname {Cu} (A)$
, there exists $t\in \operatorname {Cu} (A)$ such that $x'\ll N(n)t$
such that $x'\ll N(n)t$ and $t\ll y,\,z$
and $t\ll y,\,z$ ;
;(ii) whenever $x'\ll x$
 and $2x\ll y+2nz$
and $2x\ll y+2nz$ , there exists $g\in \operatorname {Cu} (A)$
, there exists $g\in \operatorname {Cu} (A)$ such that $2g\ll y$
such that $2g\ll y$ and $x'\ll g+M(n)z$
and $x'\ll g+M(n)z$ ;
;(iii) whenever $x_1+f,\,x_2+f\ll y$
 and $x_i'\ll x_i\ll f$
and $x_i'\ll x_i\ll f$ for $i=1,\,2$
for $i=1,\,2$ , one can find $z_1,\,z_2\in \operatorname {Cu} (A)$
, one can find $z_1,\,z_2\in \operatorname {Cu} (A)$ such that $z_1+z_2\ll y$
such that $z_1+z_2\ll y$ and $x_1'+x_2'\ll kz_1 ,\,kz_2$
and $x_1'+x_2'\ll kz_1 ,\,kz_2$ .
.
Then, $\operatorname {Cu} (A)_{\operatorname {Div}}=\operatorname {Cu} (A)$![]() .
.
Proof. Assume that (i)–(iii) are satisfied, and let $x\in \operatorname {Cu} (A)$![]() . By assumption, we have $\operatorname {div}_{m}(x)<\infty$
. By assumption, we have $\operatorname {div}_{m}(x)<\infty$![]() , which implies $\operatorname {div}_2 (x)<\infty$
, which implies $\operatorname {div}_2 (x)<\infty$![]() . Set $n:= \operatorname {div}_{2}(x)$
. Set $n:= \operatorname {div}_{2}(x)$![]() . We will show that ${\rm Div}_2(x)<\infty$
. We will show that ${\rm Div}_2(x)<\infty$![]() by proving that
by proving that
where $N_{2,n}:= (N\circ \stackrel {n}{\ldots }\circ N) (2)$![]() .
.
Let $x'\in \operatorname {Cu} (A)$![]() be such that $x'\ll x$
be such that $x'\ll x$![]() , and take $y' ,\, y$
, and take $y' ,\, y$![]() such that $x'\ll y'\ll y\ll x$
such that $x'\ll y'\ll y\ll x$![]() . Then, since $x$
. Then, since $x$![]() is $(2,\,n)$
is $(2,\,n)$![]() -divisible, we obtain $y_1,\,\ldots,\,y_n$
-divisible, we obtain $y_1,\,\ldots,\,y_n$![]() satisfying $y\ll \sum y_j$
satisfying $y\ll \sum y_j$![]() and $2y_j\leq x$
and $2y_j\leq x$![]() for each $j$
for each $j$![]() . Take $y_j'\ll y_j$
. Take $y_j'\ll y_j$![]() such that $y\ll \sum y_j'$
such that $y\ll \sum y_j'$![]() . By [Reference Thiel and Vilalta51, Lemma 2.2], for each $j$
. By [Reference Thiel and Vilalta51, Lemma 2.2], for each $j$![]() we obtain an element $r_j$
we obtain an element $r_j$![]() such that $y_j+r_j\leq x\leq 2r_j$
such that $y_j+r_j\leq x\leq 2r_j$![]() and $y_j'\leq r_j$
and $y_j'\leq r_j$![]() .
.
Using (i), we find $r\in \operatorname {Cu} (A)$![]() satisfying $y \ll N_{2,n} r$
satisfying $y \ll N_{2,n} r$![]() and $r\leq r_j$
and $r\leq r_j$![]() for every $j$
for every $j$![]() . Take $r'\ll r$
. Take $r'\ll r$![]() such that $y\ll N_{2,n} r'$
such that $y\ll N_{2,n} r'$![]() . Using (O5) at $r'\ll r\leq x$
. Using (O5) at $r'\ll r\leq x$![]() , we obtain $c\in \operatorname {Cu} (A)$
, we obtain $c\in \operatorname {Cu} (A)$![]() such that $r'+c\leq x\leq r+c$
such that $r'+c\leq x\leq r+c$![]() .
.
In particular, since one has $y_j +r\leq x\leq r+c$![]() , we obtain
, we obtain
Using (ii), we find elements $g',\,g\in \operatorname {Cu} (A)$![]() such that
such that
Applying [Reference Thiel and Vilalta51, Lemma 2.2] at $2g\ll r$![]() , we find $d\in \operatorname {Cu} (A)$
, we find $d\in \operatorname {Cu} (A)$![]() such that $g'+d\leq r\leq 2d$
such that $g'+d\leq r\leq 2d$![]() . Thus, we have $y'\ll y \leq N_{2,n} r'\leq 2N_{2,n} d$
. Thus, we have $y'\ll y \leq N_{2,n} r'\leq 2N_{2,n} d$![]() . By (i), we find $f\in \operatorname {Cu} (A)$
. By (i), we find $f\in \operatorname {Cu} (A)$![]() such that
such that
By (O6) applied at $x'\ll y'\ll g'+M(n) c$![]() , one finds elements $s',\,s,\,t',\,t\in \operatorname {Cu} (A)$
, one finds elements $s',\,s,\,t',\,t\in \operatorname {Cu} (A)$![]() such that
such that
Set $N_1:=N(\max \{ N (2N_{2,n}) ,\,M(n)\})$![]() and $N_2:=N(N (2N_{2,n}))$
and $N_2:=N(N (2N_{2,n}))$![]() . Applying (i) at $t' \ll t\leq M(n) c$
. Applying (i) at $t' \ll t\leq M(n) c$![]() and $t'\ll t\leq y'\leq N (2N_{2,n}) f$
and $t'\ll t\leq y'\leq N (2N_{2,n}) f$![]() , we obtain $x_1\in \operatorname {Cu} (A)$
, we obtain $x_1\in \operatorname {Cu} (A)$![]() such that $x_1\ll c,\,f$
such that $x_1\ll c,\,f$![]() and $t'\ll N_1 x_1$
and $t'\ll N_1 x_1$![]() . Take $x_1',\,x_1''\in \operatorname {Cu} (A)$
. Take $x_1',\,x_1''\in \operatorname {Cu} (A)$![]() such that $x_1'\ll x_1''\ll x_1$
such that $x_1'\ll x_1''\ll x_1$![]() and $t'\leq N_1x_1'$
and $t'\leq N_1x_1'$![]() .
.
Using (i) again, but this time at $s'\ll s\leq y'\leq N (2N_{2,n}) f$![]() , we obtain $x_2\in \operatorname {Cu} (A)$
, we obtain $x_2\in \operatorname {Cu} (A)$![]() such that $x_2\ll f,\,s$
such that $x_2\ll f,\,s$![]() and $s'\ll N_2 x_2$
and $s'\ll N_2 x_2$![]() . As before, take $x_2',\,x_2''\in \operatorname {Cu} (A)$
. As before, take $x_2',\,x_2''\in \operatorname {Cu} (A)$![]() such that $x_2'\ll x_2''\ll x_2$
such that $x_2'\ll x_2''\ll x_2$![]() and $s'\leq N_2x_2'$
and $s'\leq N_2x_2'$![]() .
.
One has
By (iii), we find $z_1 ,\,z_2\in \operatorname {Cu} (A)$![]() such that
such that
Applying (i) one last time, we find $z\in \operatorname {Cu} (A)$![]() such that
such that
The element $z$![]() satisfies $2z\leq z_1+z_2\leq x$
satisfies $2z\leq z_1+z_2\leq x$![]() , and
, and
as desired.
One can check that real rank zero, or stable rank one $\mathrm {C}^*$![]() -algebras satisfy (i)–(iii) in theorem 3.15 above. In particular, this recovers the discrete part of [Reference Antoine, Perera, Robert and Thiel2, Theorem 5.5].
-algebras satisfy (i)–(iii) in theorem 3.15 above. In particular, this recovers the discrete part of [Reference Antoine, Perera, Robert and Thiel2, Theorem 5.5].
Corollary 3.16 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra. Assume that $A$
-algebra. Assume that $A$![]() is either of stable rank one, or real rank zero. Then, $\operatorname {Cu} (A)_{\rm div}=\operatorname {Cu} (A)$
is either of stable rank one, or real rank zero. Then, $\operatorname {Cu} (A)_{\rm div}=\operatorname {Cu} (A)$![]() if and only if $\operatorname {Cu} (A)_{\rm Div}=\operatorname {Cu} (A)$
if and only if $\operatorname {Cu} (A)_{\rm Div}=\operatorname {Cu} (A)$![]() .
.
Proof. If $A$![]() has real rank zero, use example 3.11. For stable rank one $\mathrm {C}^*$
has real rank zero, use example 3.11. For stable rank one $\mathrm {C}^*$![]() -algebras, this just amounts to an inspection of a number of proofs:
-algebras, this just amounts to an inspection of a number of proofs:
[Reference Antoine, Perera, Robert and Thiel2, Lemma 5.3] implies that (i) is satisfied with $N=2n-1$![]() .
.
The proof of [Reference Thiel and Vilalta51, Lemma 5.5], but using weak cancellation instead of residually stably finiteness, gives (ii) in theorem 3.15 with $k=2$![]() .
.
Finally, (iii) follows from an inspection of [Reference Thiel and Vilalta49, 7.6–7.8] using that, when $A$![]() has stable rank one, (O8) can be used without the assumption of an element being idempotent; see Definition 7.2 and Proposition 7.5 in [Reference Thiel and Vilalta49] for more details.
has stable rank one, (O8) can be used without the assumption of an element being idempotent; see Definition 7.2 and Proposition 7.5 in [Reference Thiel and Vilalta49] for more details.
Remark 3.17 One can actually show that $\operatorname {Cu} (A)_{\rm mdiv}=\operatorname {Cu} (A)$![]() if and only if $\operatorname {Cu} (A)_{\rm mDiv}=\operatorname {Cu} (A)$
if and only if $\operatorname {Cu} (A)_{\rm mDiv}=\operatorname {Cu} (A)$![]() whenever $A$
whenever $A$![]() is of stable rank one. Indeed, given $x\in \operatorname {Cu} (A)$
is of stable rank one. Indeed, given $x\in \operatorname {Cu} (A)$![]() such that $\operatorname {div}_{2m}(mx)<\infty$
such that $\operatorname {div}_{2m}(mx)<\infty$![]() , it follows directly from [Reference Antoine, Perera, Robert and Thiel2, Theorem 5.5] that $\operatorname {Div}_{2m}(mx)<\infty$
, it follows directly from [Reference Antoine, Perera, Robert and Thiel2, Theorem 5.5] that $\operatorname {Div}_{2m}(mx)<\infty$![]() .
.
The same result holds for real rank zero $\mathrm {C}^*$![]() -algebras by example 3.11.
-algebras by example 3.11.
Question 3.18 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra such that $\operatorname {Cu} (A)=\operatorname {Cu}_{\rm mdiv} (A)$
-algebra such that $\operatorname {Cu} (A)=\operatorname {Cu}_{\rm mdiv} (A)$![]() . When does $A$
. When does $A$![]() satisfy $\operatorname {Cu} (A)=\operatorname {Cu}_{\rm mDiv} (A)$
satisfy $\operatorname {Cu} (A)=\operatorname {Cu}_{\rm mDiv} (A)$![]() ?
?
4. Bounded divisibility
We focus in this section on $\mathrm {C}^*$![]() -algebras where there is a global bound for the divisibility of the elements. That is, we look at those $\mathrm {C}^*$
-algebras where there is a global bound for the divisibility of the elements. That is, we look at those $\mathrm {C}^*$![]() -algebras $A$
-algebras $A$![]() such that there exist $n,\,m\in {\mathbb {N}}$
such that there exist $n,\,m\in {\mathbb {N}}$![]() with $\operatorname {div}_m ([a])\leq n$
with $\operatorname {div}_m ([a])\leq n$![]() for every $a\in A_+$
for every $a\in A_+$![]() . More generally, we focus on those that satisfy $\sup _{a\in A_+}\operatorname {div}_{2m} (m[a])<\infty$
. More generally, we focus on those that satisfy $\sup _{a\in A_+}\operatorname {div}_{2m} (m[a])<\infty$![]() for some $m\in {\mathbb {N}}$
for some $m\in {\mathbb {N}}$![]() . As we will see in theorem 5.11, these algebras will have a nowhere scattered multiplier algebra.
. As we will see in theorem 5.11, these algebras will have a nowhere scattered multiplier algebra.
We begin the section by providing sufficient conditions for this bounded divisibility to occur (propositions 4.1 and 4.3), and by showing that $\mathrm {C}^*$![]() -algebras with this property are closed under extensions (proposition 4.5). Note that we have already seen some examples, such as tracially $\mathcal {Z}$
-algebras with this property are closed under extensions (proposition 4.5). Note that we have already seen some examples, such as tracially $\mathcal {Z}$![]() -stable $\mathrm {C}^*$
-stable $\mathrm {C}^*$![]() -algebras, or $\mathrm {C}^*$
-algebras, or $\mathrm {C}^*$![]() -algebras of real rank zero; see examples 3.10 and 3.11.
-algebras of real rank zero; see examples 3.10 and 3.11.
In theorem 4.11, we prove that the set of soft elements characterizes when a $\mathrm {C}^*$![]() -algebra has multiples of bounded divisibility, and we use this to deduce the property for simple, weakly cancellative $\mathrm {C}^*$
-algebra has multiples of bounded divisibility, and we use this to deduce the property for simple, weakly cancellative $\mathrm {C}^*$![]() -algebras of Cuntz covering dimension zero; see corollary 4.13.
-algebras of Cuntz covering dimension zero; see corollary 4.13.
As mentioned in [Reference Robert and Tikuisis41], it is unclear if $\dim _{\rm nuc} (A)<\infty$![]() (with $A$
(with $A$![]() nowhere scattered) implies $\operatorname {div} (a)<\infty$
nowhere scattered) implies $\operatorname {div} (a)<\infty$![]() for every $a\in A_+$
for every $a\in A_+$![]() . However, one still gets the following result, which is a direct consequence of [Reference Robert and Tikuisis41, Proposition 3.2].
. However, one still gets the following result, which is a direct consequence of [Reference Robert and Tikuisis41, Proposition 3.2].
Proposition 4.1 Let $A$![]() be a nowhere scattered $\mathrm {C}^*$
be a nowhere scattered $\mathrm {C}^*$![]() -algebra of finite nuclear dimension at most $k$
-algebra of finite nuclear dimension at most $k$![]() . Then, for every $[a]\in \operatorname {Cu} (A)$
. Then, for every $[a]\in \operatorname {Cu} (A)$![]() , one has
, one has
In particular, one has $\operatorname {Cu} (A)=\operatorname {Cu} (A)_{\rm mdiv}$![]() .
.
Proof. If $A$![]() is nowhere scattered and of nuclear dimension at most $k$
is nowhere scattered and of nuclear dimension at most $k$![]() , so is $A\otimes \mathcal {K}$
, so is $A\otimes \mathcal {K}$![]() .
.
Let $[a]\in \operatorname {Cu} (A)$![]() . Upon passing to the hereditary $\mathrm {C}^*$
. Upon passing to the hereditary $\mathrm {C}^*$![]() -algebra $\overline {a(A\otimes \mathcal {K})a}$
-algebra $\overline {a(A\otimes \mathcal {K})a}$![]() , we may assume that $a$
, we may assume that $a$![]() is full in $A\otimes \mathcal {K}$
is full in $A\otimes \mathcal {K}$![]() ; note that $\overline {a(A\otimes \mathcal {K})a}$
; note that $\overline {a(A\otimes \mathcal {K})a}$![]() is still nowhere scattered by [Reference Thiel and Vilalta49, Proposition 4.1], and has nuclear dimension at most $k$
is still nowhere scattered by [Reference Thiel and Vilalta49, Proposition 4.1], and has nuclear dimension at most $k$![]() by [Reference Winter and Zacharias55, Proposition 2.5].
by [Reference Winter and Zacharias55, Proposition 2.5].
Recall from [Reference Thiel and Vilalta49, Theorem 3.1] that $A\otimes \mathcal {K}$![]() is nowhere scattered if and only if it has no finite-dimensional irreducible representations. By [Reference Robert and Tikuisis41, Proposition 3.2], there exists $[b]\in \operatorname {Cu} (A)$
is nowhere scattered if and only if it has no finite-dimensional irreducible representations. By [Reference Robert and Tikuisis41, Proposition 3.2], there exists $[b]\in \operatorname {Cu} (A)$![]() such that
such that
Thus, we obtain that $2(k+1)[(a-\varepsilon )_+]\leq 8(k+1)^2[b]$![]() . Since $2(k+1)[a]$
. Since $2(k+1)[a]$![]() can be written as the supremum of the elements $2(k+1)[(a-\varepsilon )_+]$
can be written as the supremum of the elements $2(k+1)[(a-\varepsilon )_+]$![]() with $\varepsilon \to 0$
with $\varepsilon \to 0$![]() , it follows that $\operatorname {div}_{4(k+1)} (2(k+1)[a])< 8(k+1)^2$
, it follows that $\operatorname {div}_{4(k+1)} (2(k+1)[a])< 8(k+1)^2$![]() , as desired.
, as desired.
Let us denote by $F(A)$![]() the central sequence algebra, as defined in [Reference Kirchberg24, Definition 1.1]. Given a separable, unital $\mathrm {C}^*$
the central sequence algebra, as defined in [Reference Kirchberg24, Definition 1.1]. Given a separable, unital $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() , it is not known if $A$
, it is not known if $A$![]() being $\mathcal {Z}$
being $\mathcal {Z}$![]() -stable is equivalent to $F(A)$
-stable is equivalent to $F(A)$![]() admitting no characters; see [Reference Kirchberg and Rørdam26]. Although this question remains open, one does have the following result from [Reference Christensen12, Part II, Article B, Proposition 2.8].
admitting no characters; see [Reference Kirchberg and Rørdam26]. Although this question remains open, one does have the following result from [Reference Christensen12, Part II, Article B, Proposition 2.8].
Proposition 4.2 [Reference Christensen12]
Let $A$![]() be a separable $\mathrm {C}^*$
be a separable $\mathrm {C}^*$![]() -algebra. Assume that $F(A)$
-algebra. Assume that $F(A)$![]() admits no characters. Then, for every $m\in {\mathbb {N}}$
admits no characters. Then, for every $m\in {\mathbb {N}}$![]() there exists $n$
there exists $n$![]() such that $\operatorname {div}_m ([a])\leq n$
such that $\operatorname {div}_m ([a])\leq n$![]() for all $a\in A_+$
for all $a\in A_+$![]() .
.
Proof. It follows from [Reference Robert and Rørdam40, Corollary 5.6] that $F(A)$![]() has no characters if and only if $\operatorname {div}_2 ([1])<\infty$
has no characters if and only if $\operatorname {div}_2 ([1])<\infty$![]() in $\operatorname {Cu} (F(A))$
in $\operatorname {Cu} (F(A))$![]() . Let $n_0=\operatorname {div}_2 ([1])$
. Let $n_0=\operatorname {div}_2 ([1])$![]() . [Reference Christensen12, Part II, B, Proposition 2.8] implies that $\operatorname {div}_2 ([a])\leq n_0$
. [Reference Christensen12, Part II, B, Proposition 2.8] implies that $\operatorname {div}_2 ([a])\leq n_0$![]() for every $a\in A_+$
for every $a\in A_+$![]() .
.
An inductive argument now shows that $\sup _{a\in A_+}\operatorname {div}_m ([a])<\infty$![]() for every $m\in {\mathbb {N}}$
for every $m\in {\mathbb {N}}$![]() ; see, for example, [Reference Thiel and Vilalta51, Lemma 3.4].
; see, for example, [Reference Thiel and Vilalta51, Lemma 3.4].
Given $[a],\,[b]\in \operatorname {Cu} (A)$![]() , recall that we write $[a]<_s [b]$
, recall that we write $[a]<_s [b]$![]() whenever there exists $\gamma <1$
whenever there exists $\gamma <1$![]() such that $\lambda ([a])\leq \gamma \lambda ([b])$
such that $\lambda ([a])\leq \gamma \lambda ([b])$![]() for every $\lambda \in F(\operatorname {Cu} (A))\cong {\rm QT}(A)$
for every $\lambda \in F(\operatorname {Cu} (A))\cong {\rm QT}(A)$![]() ; see [Reference Robert and Tikuisis41, 2.1].
; see [Reference Robert and Tikuisis41, 2.1].
Let $k\in {\mathbb {N}}$![]() . As defined in [Reference Winter54, Definition 2.1], a $\mathrm {C}^*$
. As defined in [Reference Winter54, Definition 2.1], a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() is said to have $k$
is said to have $k$![]() -comparison if for every $[a],\,[b_0],\,\ldots,\,[b_k]\in \operatorname {Cu} (A)$
-comparison if for every $[a],\,[b_0],\,\ldots,\,[b_k]\in \operatorname {Cu} (A)$![]() such that $[a]<_s [b_i]$
such that $[a]<_s [b_i]$![]() for all $i$
for all $i$![]() , we have $[a]\leq \sum _i [b_i]$
, we have $[a]\leq \sum _i [b_i]$![]() .
.
Also recall that $A$![]() has a surjective rank map if every element in $L (F(\operatorname {Cu} (A)))$
has a surjective rank map if every element in $L (F(\operatorname {Cu} (A)))$![]() can be realized as a rank function; see [Reference Antoine, Perera, Robert and Thiel2, Section 7] for details.
can be realized as a rank function; see [Reference Antoine, Perera, Robert and Thiel2, Section 7] for details.
Proposition 4.3 Let $A$![]() be a nowhere scattered $\mathrm {C}^*$
be a nowhere scattered $\mathrm {C}^*$![]() -algebra with $k$
-algebra with $k$![]() -comparison. Assume that the family of separable sub-$\mathrm {C}^*$
-comparison. Assume that the family of separable sub-$\mathrm {C}^*$![]() -algebras of $A$
-algebras of $A$![]() with a surjective rank map is $\sigma$
with a surjective rank map is $\sigma$![]() -complete and cofinal. Then, $\operatorname {Div}_{2(k+1)}((k+1)[a])\leq 4(k+1)^3$
-complete and cofinal. Then, $\operatorname {Div}_{2(k+1)}((k+1)[a])\leq 4(k+1)^3$![]() for every $[a]\in \operatorname {Cu} (A)$
for every $[a]\in \operatorname {Cu} (A)$![]() .
.
Proof. Let $x:=[a]$![]() . By [Reference Thiel and Vilalta48, Proposition 6.1] and [Reference Farah, Hart, Lupini, Robert, Tikuisis, Vignati and Winter20, Proposition 3.8.1], there exists a separable sub-$\mathrm {C}^*$
. By [Reference Thiel and Vilalta48, Proposition 6.1] and [Reference Farah, Hart, Lupini, Robert, Tikuisis, Vignati and Winter20, Proposition 3.8.1], there exists a separable sub-$\mathrm {C}^*$![]() -algebra $B\subseteq A$
-algebra $B\subseteq A$![]() that has a surjective rank map, is nowhere scattered, contains $x$
that has a surjective rank map, is nowhere scattered, contains $x$![]() and is such that the induced inclusion map $\operatorname {Cu} (B)\to \operatorname {Cu} (A)$
and is such that the induced inclusion map $\operatorname {Cu} (B)\to \operatorname {Cu} (A)$![]() is an order-embedding.
is an order-embedding.
By definition, every element in $L (F(\operatorname {Cu} (B)))$![]() can be realized as a rank function. Thus, there exists $y\in \operatorname {Cu} (B)$
can be realized as a rank function. Thus, there exists $y\in \operatorname {Cu} (B)$![]() such that $\widehat {y}=\frac {1}{3(k+1)}\widehat {x}$
such that $\widehat {y}=\frac {1}{3(k+1)}\widehat {x}$![]() . This implies, in particular, that
. This implies, in particular, that
Applying $k$![]() -comparison, one obtains $2(k+1)y\leq (k+1)x$
-comparison, one obtains $2(k+1)y\leq (k+1)x$![]() and $x\leq 4(k+1)^2 y$
and $x\leq 4(k+1)^2 y$![]() in $\operatorname {Cu} (B)$
in $\operatorname {Cu} (B)$![]() . Using that the map $\operatorname {Cu} (B)\to \operatorname {Cu} (A)$
. Using that the map $\operatorname {Cu} (B)\to \operatorname {Cu} (A)$![]() is an order-embedding, the same is true in $\operatorname {Cu} (A)$
is an order-embedding, the same is true in $\operatorname {Cu} (A)$![]() . Thus, we have
. Thus, we have
as desired.
Remark 4.4 As shown in [Reference Antoine, Perera, Robert and Thiel2, Theorem 7.14], a separable, nowhere scattered $\mathrm {C}^*$![]() -algebra of stable rank one always has a surjective rank map. Thus, proposition 4.3 above applies to all stable rank one $\mathrm {C}^*$
-algebra of stable rank one always has a surjective rank map. Thus, proposition 4.3 above applies to all stable rank one $\mathrm {C}^*$![]() -algebras with $k$
-algebras with $k$![]() -comparison.
-comparison.
In fact, it was shown in [Reference Antoine, Perera, Robert and Thiel2, Theorem 8.12] that a separable, nowhere scattered $\mathrm {C}^*$![]() -algebra of stable rank one has $k$
-algebra of stable rank one has $k$![]() -comparison if and only if it has strict comparison. Consequently, we get that $\operatorname {div}_2 (x)\leq 4$
-comparison if and only if it has strict comparison. Consequently, we get that $\operatorname {div}_2 (x)\leq 4$![]() for every $x\in \operatorname {Cu} (A)$
for every $x\in \operatorname {Cu} (A)$![]() . Further, a small modification of the proof shows that $\operatorname {Cu} (A)$
. Further, a small modification of the proof shows that $\operatorname {Cu} (A)$![]() is almost divisible (i.e. $0$
is almost divisible (i.e. $0$![]() -almost divisible). Indeed, following the notation of the proof, given any $x\in \operatorname {Cu} (A)$
-almost divisible). Indeed, following the notation of the proof, given any $x\in \operatorname {Cu} (A)$![]() and any $k\in {\mathbb {N}}$
and any $k\in {\mathbb {N}}$![]() find $y\in \operatorname {Cu} (B)$
find $y\in \operatorname {Cu} (B)$![]() such that $\widehat {y}=\frac {2}{2k+1}\widehat {x}$
such that $\widehat {y}=\frac {2}{2k+1}\widehat {x}$![]() . A direct computation shows that
. A direct computation shows that
Using strict comparison, one gets $ky\leq x\leq (k+1)y$![]() , as desired.
, as desired.
The following is a generalization of [Reference Thiel and Vilalta49, Proposition 4.2].
Proposition 4.5 Let $I$![]() be an ideal of a $\mathrm {C}^*$
be an ideal of a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() . Assume that there exist $m_0,\,m_1,\,n_0,\,n_1\in {\mathbb {N}}$
. Assume that there exist $m_0,\,m_1,\,n_0,\,n_1\in {\mathbb {N}}$![]() such that
such that
for every $a\in (A/I)_+$![]() and every $b\in I_+$
and every $b\in I_+$![]() . Then,
. Then,
for every $c\in A_+$![]() .
.
Conversely, $\operatorname {div}_{2m}(m[a]),\,\operatorname {div}_{2m}(m[b])\leq n$![]() for every $a\in (A/I)_+$
for every $a\in (A/I)_+$![]() and $b\in I_+$
and $b\in I_+$![]() whenever $\sup _{c\in A_+}\operatorname {div}_{2m}(m[c])\leq n$
whenever $\sup _{c\in A_+}\operatorname {div}_{2m}(m[c])\leq n$![]() for some $m,\,n\in {\mathbb {N}}$
for some $m,\,n\in {\mathbb {N}}$![]() .
.
Proof. It follows from [Reference Ciuperca, Robert and Santiago13] that $\operatorname {Cu} (I)$![]() can be identified with an ideal of $\operatorname {Cu} (A)$
can be identified with an ideal of $\operatorname {Cu} (A)$![]() , and that $\operatorname {Cu} (A/I)$
, and that $\operatorname {Cu} (A/I)$![]() is naturally isomorphic to the quotient $\operatorname {Cu} (A)/\operatorname {Cu} (I)$
is naturally isomorphic to the quotient $\operatorname {Cu} (A)/\operatorname {Cu} (I)$![]() . We will make these identifications without explicitly writing the isomorphisms.
. We will make these identifications without explicitly writing the isomorphisms.
Let $c\in A_+$![]() , and set $x:=[c]$
, and set $x:=[c]$![]() . Denote by $\operatorname {Cu} (\pi )\colon \operatorname {Cu} (A)\to \operatorname {Cu} (A/I)$
. Denote by $\operatorname {Cu} (\pi )\colon \operatorname {Cu} (A)\to \operatorname {Cu} (A/I)$![]() the induced quotient map. Given $x',\,x''$
the induced quotient map. Given $x',\,x''$![]() in $\operatorname {Cu} (A)$
in $\operatorname {Cu} (A)$![]() such that $x'\ll x''\ll x$
such that $x'\ll x''\ll x$![]() , we can apply the bounded divisibility of $\operatorname {Cu} (A/I)$
, we can apply the bounded divisibility of $\operatorname {Cu} (A/I)$![]() to obtain elements $y_j'',\,y_j',\,y_j\in \operatorname {Cu} (A)$
to obtain elements $y_j'',\,y_j',\,y_j\in \operatorname {Cu} (A)$![]() for $j=1,\,\ldots,\,n_0$
for $j=1,\,\ldots,\,n_0$![]() such that
such that
and $y_j''\ll y_j '\ll y_j$![]() for each $j$
for each $j$![]() . Note that this is possible because $\operatorname {Cu} (\pi ) (x)=[\pi (c)]$
. Note that this is possible because $\operatorname {Cu} (\pi ) (x)=[\pi (c)]$![]() and $\operatorname {Cu} (\pi ) (x)$
and $\operatorname {Cu} (\pi ) (x)$![]() has a representative in $(A/I)_+$
has a representative in $(A/I)_+$![]() .
.
Take $w\in \operatorname {Cu} (I)$![]() such that $w=2w$
such that $w=2w$![]() , and
, and
Using [Reference Thiel and Vilalta49, Proposition 7.8], we find elements $z_j',\, z_j\in \operatorname {Cu} (A)$![]() satisfying
satisfying
for every $j=1,\,\ldots,\,n_0$![]() .
.
In particular, we have
Applying (O6), we obtain an element $\tilde {r}\in \operatorname {Cu} (A)$![]() such that
such that
Note that, since $\tilde {r}\leq x''\ll [c]$![]() with $c\in A_+$
with $c\in A_+$![]() , there exists $b\in A_+$
, there exists $b\in A_+$![]() such that $r:=[b]$
such that $r:=[b]$![]() satisfies $r\leq \tilde {r}$
satisfies $r\leq \tilde {r}$![]() and $x'\ll z_1'+\ldots + z_{n_0 }' +r$
and $x'\ll z_1'+\ldots + z_{n_0 }' +r$![]() ; see, for example, [Reference Thiel and Vilalta49, Lemma 3.3(1)]. Further, since we also have $[b]\leq w$
; see, for example, [Reference Thiel and Vilalta49, Lemma 3.3(1)]. Further, since we also have $[b]\leq w$![]() , one gets $b\in I_+$
, one gets $b\in I_+$![]() . Take $r'\ll r$
. Take $r'\ll r$![]() such that $x'\leq z_1'+\ldots + z_{n_0}' +r'$
such that $x'\leq z_1'+\ldots + z_{n_0}' +r'$![]() .
.
Now, using that $\operatorname {div}_{2m_1}(m_1[b])\leq n_1$![]() , one gets elements $r_1,\,\ldots,\, r_{n_1}$
, one gets elements $r_1,\,\ldots,\, r_{n_1}$![]() such that
such that
for each $i\leq n_1$![]() .
.
Thus, it follows that
and
for each $i$![]() and $j$
and $j$![]() .
.
This proves that
as desired.
The converse follows from a standard argument; see [Reference Thiel and Vilalta51, Proposition 3.9].
The previous result also works, mutatis-mutandis, with $\operatorname {Div} ()$![]() instead of $\operatorname {div} ()$
instead of $\operatorname {div} ()$![]() . In this case, an inspection of [Reference Thiel and Vilalta51, Theorem 3.10] gives the following:
. In this case, an inspection of [Reference Thiel and Vilalta51, Theorem 3.10] gives the following:
Theorem 4.6 Let $I$![]() be an ideal of a $\mathrm {C}^*$
be an ideal of a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() . Assume that there exist $m_0,\,m_1,\,n_0,\,n_1\in {\mathbb {N}}$
. Assume that there exist $m_0,\,m_1,\,n_0,\,n_1\in {\mathbb {N}}$![]() such that
such that
for every $a\in I_+$![]() and every $b\in (A/I)_+$
and every $b\in (A/I)_+$![]() . Then, there exist $M,\,N\in {\mathbb {N}}$
. Then, there exist $M,\,N\in {\mathbb {N}}$![]() depending only on $m_0,\,m_1,\,n_0,\,n_1$
depending only on $m_0,\,m_1,\,n_0,\,n_1$![]() such that
such that
for every $c\in A_+$![]() .
.
Conversely, $\operatorname {Div}_{2m}(m[a]),\,\operatorname {Div}_{2m}(m[b])\leq n$![]() for every $a\in (A/I)_+$
for every $a\in (A/I)_+$![]() and $b\in I_+$
and $b\in I_+$![]() whenever $\sup _{c\in A_+}\operatorname {Div}_{2m}(m[c])\leq n$
whenever $\sup _{c\in A_+}\operatorname {Div}_{2m}(m[c])\leq n$![]() for some $m,\,n\in {\mathbb {N}}$
for some $m,\,n\in {\mathbb {N}}$![]() .
.
Proof. Assume first that $I$![]() and $A/I$
and $A/I$![]() satisfy the stated conditions. Let $c\in A_+$
satisfy the stated conditions. Let $c\in A_+$![]() and take $\varepsilon >0$
and take $\varepsilon >0$![]() . Set
. Set
As before, denote by $\pi$![]() the induced quotient map $\operatorname {Cu} (A)\to \operatorname {Cu} (A/I)$
the induced quotient map $\operatorname {Cu} (A)\to \operatorname {Cu} (A/I)$![]() . Applying $\operatorname {Div}_{4m_1} (m_1\pi (x))\leq n_1$
. Applying $\operatorname {Div}_{4m_1} (m_1\pi (x))\leq n_1$![]() to $\pi (x'')\ll \pi (x)$
to $\pi (x'')\ll \pi (x)$![]() , we find $y\in \operatorname {Cu} (A)$
, we find $y\in \operatorname {Cu} (A)$![]() such that
such that
Take $y',\,y''\in \operatorname {Cu} (A)$![]() such that $y'\ll y''\ll y$
such that $y'\ll y''\ll y$![]() and $m_1\pi (x'')\leq n_1\pi (y')$
and $m_1\pi (x'')\leq n_1\pi (y')$![]() . Find $w\in \operatorname {Cu} (I)$
. Find $w\in \operatorname {Cu} (I)$![]() such that
such that
Applying [Reference Thiel and Vilalta49, Proposition 7.8] at the first inequality and the pair $y'\ll y''$![]() , we find $z\in \operatorname {Cu} (A)$
, we find $z\in \operatorname {Cu} (A)$![]() satisfying
satisfying
Choose $z'\in \operatorname {Cu} (A)$![]() such that $z'\ll z$
such that $z'\ll z$![]() and $y'\ll z'+w$
and $y'\ll z'+w$![]() . Note that we have
. Note that we have
Further, using that $y'\ll z'+w$![]() , we obtain
, we obtain
Applying (O6), we find $\tilde {r}\in S$![]() such that
such that
Proceeding as in the previous proof, note that, since $x''=[(c-\varepsilon )_+ ]$![]() and $\tilde {r}\leq w\in \operatorname {Cu} (I)$
and $\tilde {r}\leq w\in \operatorname {Cu} (I)$![]() , we can find $a\in I_+$
, we can find $a\in I_+$![]() such that $r:=[a]$
such that $r:=[a]$![]() satisfies $r\leq \tilde {r}$
satisfies $r\leq \tilde {r}$![]() and $x'\ll n_1 z' + r$
and $x'\ll n_1 z' + r$![]() . Take $r'$
. Take $r'$![]() with $r'\ll r$
with $r'\ll r$![]() and $x'\ll n_1 z' + r'$
and $x'\ll n_1 z' + r'$![]() .
.
Applying $\operatorname {Div}_{4m_0} (m_0 r)\leq n_0$![]() to $m_0 r'\ll m_0 r$
to $m_0 r'\ll m_0 r$![]() , we get $t\in \operatorname {Cu} (I)$
, we get $t\in \operatorname {Cu} (I)$![]() such that
such that
Recall that $r\leq x$![]() . Combining (4.1) and (4.2) we obtain
. Combining (4.1) and (4.2) we obtain
One also gets
which shows that $\operatorname {Div}_{4m_0m_1}(2m_0m_1 x)\leq 2m_0 m_1 n_0n_1$![]() , as desired.
, as desired.
As in the proof of the previous proposition, we note that the converse follows from similar arguments to those in [Reference Thiel and Vilalta51, Proposition 3.9].
As noted in lemma 3.12, having a sup-dense subset of elements with finite weak divisibility does not imply that every element has such property. However, proposition 4.8 below shows that it is enough to check finite weak divisibility for strongly soft elements (which, in general, are not sup-dense).
4.7. Strongly soft elements and retracts
Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra. As defined in [Reference Thiel and Vilalta52], we denote by $\operatorname {Cu} (A)_{\rm {soft}}$
-algebra. As defined in [Reference Thiel and Vilalta52], we denote by $\operatorname {Cu} (A)_{\rm {soft}}$![]() the set of strongly soft elements, that is, those elements $x\in \operatorname {Cu} (A)$
the set of strongly soft elements, that is, those elements $x\in \operatorname {Cu} (A)$![]() such that for every $x'\ll x$
such that for every $x'\ll x$![]() there exists $t\in \operatorname {Cu} (A)$
there exists $t\in \operatorname {Cu} (A)$![]() satisfying $x'+t\leq x\leq \infty t$
satisfying $x'+t\leq x\leq \infty t$![]() . When $A$
. When $A$![]() is residually stably finite, $[a]\in \operatorname {Cu} (A)$
is residually stably finite, $[a]\in \operatorname {Cu} (A)$![]() is strongly soft if and only if $\overline {aAa}$
is strongly soft if and only if $\overline {aAa}$![]() has no nonzero, unital quotients; see [Reference Thiel and Vilalta52, Proposition 4.16].
has no nonzero, unital quotients; see [Reference Thiel and Vilalta52, Proposition 4.16].
Under certain assumptions, given any $x\in \operatorname {Cu} (A)$![]() one can find the largest strongly soft element below $x$
one can find the largest strongly soft element below $x$![]() . When this is the case, we denote by $\sigma \colon \operatorname {Cu} (A)\to \operatorname {Cu} (A)_{\rm {soft}}$
. When this is the case, we denote by $\sigma \colon \operatorname {Cu} (A)\to \operatorname {Cu} (A)_{\rm {soft}}$![]() the map that sends an element $x$
the map that sends an element $x$![]() to the largest strongly soft element dominated by $x$
to the largest strongly soft element dominated by $x$![]() .
.
In [Reference Asadi-Vasfi, Thiel and Vilalta6, Theorem 5.6], it is shown that $\sigma$![]() can always be defined whenever $A$
can always be defined whenever $A$![]() is separable, has the Global Glimm Property and its Cuntz semigroup is left-soft separative, that is, if for any triplet of elements $y,\,t\in S$
is separable, has the Global Glimm Property and its Cuntz semigroup is left-soft separative, that is, if for any triplet of elements $y,\,t\in S$![]() and $x\in S_{\rm {soft}}$
and $x\in S_{\rm {soft}}$![]() satisfying
satisfying
we have $x\ll y$![]() ; see [Reference Asadi-Vasfi, Thiel and Vilalta6, Definition 3.2]. As explained in [Reference Asadi-Vasfi, Thiel and Vilalta6, Section 3], $\mathrm {C}^*$
; see [Reference Asadi-Vasfi, Thiel and Vilalta6, Definition 3.2]. As explained in [Reference Asadi-Vasfi, Thiel and Vilalta6, Section 3], $\mathrm {C}^*$![]() -algebras with strict comparison or stable rank one have a left-soft separative Cuntz semigroup.
-algebras with strict comparison or stable rank one have a left-soft separative Cuntz semigroup.
In this case, $\sigma$![]() is an order- and suprema-preserving superadditive map that satisfies $x\leq \sigma (x)+t$
is an order- and suprema-preserving superadditive map that satisfies $x\leq \sigma (x)+t$![]() whenever $x\leq \infty t$
whenever $x\leq \infty t$![]() . Recall that a map $\phi$
. Recall that a map $\phi$![]() is superadditive if $\phi (x+y)\leq \phi (x)+\phi (y)$
is superadditive if $\phi (x+y)\leq \phi (x)+\phi (y)$![]() .
.
Proposition 4.8 Let $A$![]() be a separable $\mathrm {C}^*$
be a separable $\mathrm {C}^*$![]() -algebra with the Global Glimm Property such that $\operatorname {Cu} (A)$
-algebra with the Global Glimm Property such that $\operatorname {Cu} (A)$![]() is left-soft separative, and let $x\in \operatorname {Cu} (A)$
is left-soft separative, and let $x\in \operatorname {Cu} (A)$![]() and $m\in {\mathbb {N}}$
and $m\in {\mathbb {N}}$![]() . Then
. Then
Proof. First, to see that $\operatorname {div}_m(\sigma (x))\leq \operatorname {div}_m(x)+1$![]() , assume that $\operatorname {div}_m(x)=n$
, assume that $\operatorname {div}_m(x)=n$![]() for some $n\in {\mathbb {N}}$
for some $n\in {\mathbb {N}}$![]() , since otherwise there is nothing to prove.
, since otherwise there is nothing to prove.
Let $s\ll \sigma (x)$![]() . Using that $\sigma$
. Using that $\sigma$![]() preserves suprema of increasing sequences, we can find $x'\ll x$
preserves suprema of increasing sequences, we can find $x'\ll x$![]() such that $s\ll \sigma (x')$
such that $s\ll \sigma (x')$![]() .
.
Since $A$![]() satisfies the Global Glimm Property, one can use [Reference Thiel and Vilalta52, Proposition 7.7] to deduce that there exists $t\in \operatorname {Cu} (A)_{\rm {soft}}$
satisfies the Global Glimm Property, one can use [Reference Thiel and Vilalta52, Proposition 7.7] to deduce that there exists $t\in \operatorname {Cu} (A)_{\rm {soft}}$![]() such that $(nm)t\leq x\leq \infty t$
such that $(nm)t\leq x\leq \infty t$![]() . Note that $(nm)t\leq \sigma (x)$
. Note that $(nm)t\leq \sigma (x)$![]() because $t$
because $t$![]() is strongly soft. Using that $x$
is strongly soft. Using that $x$![]() is weakly $(m,\,n)$
is weakly $(m,\,n)$![]() -divisible, one finds $z_1,\,\ldots,\,z_n\in \operatorname {Cu} (A)$
-divisible, one finds $z_1,\,\ldots,\,z_n\in \operatorname {Cu} (A)$![]() such that
such that
for every $j$![]() .
.
Now, using that $z_i\leq \infty t$![]() for every $i$
for every $i$![]() and that $\operatorname {Cu} (A)$
and that $\operatorname {Cu} (A)$![]() is left-soft separative, we obtain
is left-soft separative, we obtain
Further, using that $\sigma$![]() is superadditive, we also get $m\sigma (z_j)\leq \sigma (mz_j)\leq \sigma (x)$
is superadditive, we also get $m\sigma (z_j)\leq \sigma (mz_j)\leq \sigma (x)$![]() . Since $n(mt)\leq \sigma (x)$
. Since $n(mt)\leq \sigma (x)$![]() , we deduce that $\operatorname {div}_n(\sigma (x))\leq n+1$
, we deduce that $\operatorname {div}_n(\sigma (x))\leq n+1$![]() , as desired.
, as desired.
To prove that $\operatorname {div}_m(x)\leq \operatorname {div}_m(\sigma (x))+1$![]() , take $t\in \operatorname {Cu} (A)$
, take $t\in \operatorname {Cu} (A)$![]() such that $mt\leq x\leq \infty t$
such that $mt\leq x\leq \infty t$![]() . Note that this can be done because $A$
. Note that this can be done because $A$![]() has the Global Glimm Property and, consequently, $\operatorname {Cu} (A)$
has the Global Glimm Property and, consequently, $\operatorname {Cu} (A)$![]() is $(m,\,\omega )$
is $(m,\,\omega )$![]() -divisible; see paragraph 2.3. Using that $x\leq \infty t$
-divisible; see paragraph 2.3. Using that $x\leq \infty t$![]() , we have $x\leq \sigma (x)+t$
, we have $x\leq \sigma (x)+t$![]() . Let $x'\ll x$
. Let $x'\ll x$![]() . Since $x'\ll \sigma (x)+t$
. Since $x'\ll \sigma (x)+t$![]() , we can use (O6) to obtain an element $y$
, we can use (O6) to obtain an element $y$![]() such that $x'\ll y+t$
such that $x'\ll y+t$![]() with $y\ll \sigma (x)$
with $y\ll \sigma (x)$![]() .
.
Let $n$![]() be such that $\sigma (x)$
be such that $\sigma (x)$![]() is weakly $(m,\,n)$
is weakly $(m,\,n)$![]() -divisible. Then, there exist $z_1,\,\ldots,\,z_n$
-divisible. Then, there exist $z_1,\,\ldots,\,z_n$![]() satisfying
satisfying
for each $j$![]() .
.
We obtain
for every $j$![]() , which implies that $\operatorname {div}_m(x)\leq n+1$
, which implies that $\operatorname {div}_m(x)\leq n+1$![]() .
.
Lemma 4.9 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra, and let $s,\,t\in \operatorname {Cu} (A)$
-algebra, and let $s,\,t\in \operatorname {Cu} (A)$![]() . Assume that $s$
. Assume that $s$![]() is strongly soft. Then, the element $s\wedge \infty t$
is strongly soft. Then, the element $s\wedge \infty t$![]() is strongly soft in $\operatorname {Cu} (A)$
is strongly soft in $\operatorname {Cu} (A)$![]() .
.
Proof. Let $x',\,x\in \operatorname {Cu} (A)$![]() be such that $x'\ll x\ll s\wedge \infty t$
be such that $x'\ll x\ll s\wedge \infty t$![]() . By definition, this implies that $x'\ll s$
. By definition, this implies that $x'\ll s$![]() and $x'\ll \infty t$
and $x'\ll \infty t$![]() .
.
Since $s$![]() is strongly soft, we find $y\in \operatorname {Cu} (A)$
is strongly soft, we find $y\in \operatorname {Cu} (A)$![]() such that $x'+y\leq s\leq \infty y$
such that $x'+y\leq s\leq \infty y$![]() . Thus, using that taking infima with an idempotent is a monoid morphism ([Reference Antoine, Perera, Robert and Thiel1, Section 2]), we have
. Thus, using that taking infima with an idempotent is a monoid morphism ([Reference Antoine, Perera, Robert and Thiel1, Section 2]), we have
This shows that $s\wedge \infty t$![]() is strongly soft.
is strongly soft.
Lemma 4.10 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra with the Global Glimm Property. Then, for $x',\, x\in \operatorname {Cu} (A)$
-algebra with the Global Glimm Property. Then, for $x',\, x\in \operatorname {Cu} (A)$![]() such that $x'\ll x$
such that $x'\ll x$![]() , there exist $s_1 ,\, s_2 \in \operatorname {Cu} (A)_{\rm {soft}}$
, there exist $s_1 ,\, s_2 \in \operatorname {Cu} (A)_{\rm {soft}}$![]() such that $s_1 ,\, s_2 \leq x$
such that $s_1 ,\, s_2 \leq x$![]() and $x' \leq s_1 + s_2$
and $x' \leq s_1 + s_2$![]() .
.
Proof. Let $x',\,x\in \operatorname {Cu} (A)$![]() satisfy $x'\ll x$
satisfy $x'\ll x$![]() . It follows from [Reference Thiel and Vilalta52, Proposition 7.7] that there exists $y\in \operatorname {Cu} (A)_{\rm {soft}}$
. It follows from [Reference Thiel and Vilalta52, Proposition 7.7] that there exists $y\in \operatorname {Cu} (A)_{\rm {soft}}$![]() satisfying $y\leq x\leq \infty y$
satisfying $y\leq x\leq \infty y$![]() . In particular, one has $x'\ll \infty y$
. In particular, one has $x'\ll \infty y$![]() .
.
By [Reference Thiel and Vilalta52, Proposition 5.6], we can take $y',\,y''\in \operatorname {Cu} (A)_{\rm {soft}}$![]() such that $y'\ll y''\ll y$
such that $y'\ll y''\ll y$![]() and $x'\ll \infty y'$
and $x'\ll \infty y'$![]() . Since $y''$
. Since $y''$![]() is soft, we find $t\in \operatorname {Cu} (A)_{\rm {soft}}$
is soft, we find $t\in \operatorname {Cu} (A)_{\rm {soft}}$![]() such that $y'+t\leq y''\leq \infty t$
such that $y'+t\leq y''\leq \infty t$![]() ; see [Reference Thiel and Vilalta52, Proposition 4.13]. Now, by (O5) applied to $y''\ll y\leq x$
; see [Reference Thiel and Vilalta52, Proposition 4.13]. Now, by (O5) applied to $y''\ll y\leq x$![]() , there exists $c\in \operatorname {Cu} (A)$
, there exists $c\in \operatorname {Cu} (A)$![]() satisfying
satisfying
Thus, we have
Using that $x'\leq \infty y'$![]() , we obtain
, we obtain
and
By lemma 4.9, the elements $y\wedge \infty y''$![]() and $t\wedge \infty y''$
and $t\wedge \infty y''$![]() are strongly soft. Further, note that one gets
are strongly soft. Further, note that one gets
with $c\wedge \infty y''\leq \infty y''\leq \infty (t\wedge \infty y'')$![]() .
.
Using [Reference Thiel and Vilalta52, Theorem 4.14(2)], we deduce that $(c+t)\wedge \infty y''$![]() is also strongly soft. Set $s_1:=y\wedge \infty y''$
is also strongly soft. Set $s_1:=y\wedge \infty y''$![]() and $s_2:=(c+t)\wedge \infty y''$
and $s_2:=(c+t)\wedge \infty y''$![]() . We have $s_1,\,s_2\in \operatorname {Cu} (A)_{\rm {soft}}$
. We have $s_1,\,s_2\in \operatorname {Cu} (A)_{\rm {soft}}$![]() ,
,
as required.
When $\operatorname {Cu} (A)$![]() is not left-soft separative, we still have the following:
is not left-soft separative, we still have the following:
Theorem 4.11 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra with the Global Glimm Property, and let $m\in {\mathbb {N}}$
-algebra with the Global Glimm Property, and let $m\in {\mathbb {N}}$![]() . Then, the following are equivalent:
. Then, the following are equivalent:
(i) there exists $n\in {\mathbb {N}}$
 such that $\operatorname {div}_{2m} (m[a])\leq n$
such that $\operatorname {div}_{2m} (m[a])\leq n$ for every $[a]\in \operatorname {Cu} (A)$
for every $[a]\in \operatorname {Cu} (A)$ ;
;(ii) there exists $n\in {\mathbb {N}}$
 such that $\operatorname {div}_{2m} (m[a])\leq n$
such that $\operatorname {div}_{2m} (m[a])\leq n$ for every $[a]\in \operatorname {Cu} (A)_{\rm {soft}}$
for every $[a]\in \operatorname {Cu} (A)_{\rm {soft}}$ .
.
Proof. That (i) implies (ii) is trivial.
To prove the converse, let $x',\,x\in \operatorname {Cu} (A)$![]() be such that $x'\ll x$
be such that $x'\ll x$![]() . Using lemma 4.10, one finds $s_1,\,s_2\in \operatorname {Cu} (A)_{\rm {soft}}$
. Using lemma 4.10, one finds $s_1,\,s_2\in \operatorname {Cu} (A)_{\rm {soft}}$![]() satisfying $s_1 ,\,s_2\leq x$
satisfying $s_1 ,\,s_2\leq x$![]() and $x'\leq s_1+s_2$
and $x'\leq s_1+s_2$![]() . In particular, $ms_1,\,ms_2\leq mx$
. In particular, $ms_1,\,ms_2\leq mx$![]() and $mx'\leq ms_1+ms_2$
and $mx'\leq ms_1+ms_2$![]() .
.
By lemma 3.3 (ii), we have
as desired.
Corollary 4.12 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra with the Global Glimm Property. Assume that $\operatorname {Cu} (A)_{\rm {soft}}$
-algebra with the Global Glimm Property. Assume that $\operatorname {Cu} (A)_{\rm {soft}}$![]() is a retract of a Cu-semigroup $S$
is a retract of a Cu-semigroup $S$![]() satisfying $\sup _{s\in S}\operatorname {div}_{2k} (ks)<\infty$
satisfying $\sup _{s\in S}\operatorname {div}_{2k} (ks)<\infty$![]() for some $k\in {\mathbb {N}}$
for some $k\in {\mathbb {N}}$![]() . Then, there exist $n,\,m\in {\mathbb {N}}$
. Then, there exist $n,\,m\in {\mathbb {N}}$![]() such that $\operatorname {div}_{2m} (m[a])\leq n$
such that $\operatorname {div}_{2m} (m[a])\leq n$![]() for every $[a]\in \operatorname {Cu} (A)$
for every $[a]\in \operatorname {Cu} (A)$![]() .
.
Proof. Using that $\operatorname {Cu} (A)_{\rm {soft}}$![]() is a retract of $S$
is a retract of $S$![]() , it follows that
, it follows that
for every $y \in \operatorname {Cu} (A)_{\rm {soft}}$![]() .
.
Applying theorem 4.11, there exist $n,\,m\in {\mathbb {N}}$![]() such that $\operatorname {div}_{2m}(m x)\leq n$
such that $\operatorname {div}_{2m}(m x)\leq n$![]() for every $x\in \operatorname {Cu} (A)$
for every $x\in \operatorname {Cu} (A)$![]() .
.
Recall from [Reference Thiel and Vilalta50, Definition 3.1] that one says that $\operatorname {Cu} (A)$![]() has covering dimension zero if, whenever $x'\ll x\ll y_1+y_2$
has covering dimension zero if, whenever $x'\ll x\ll y_1+y_2$![]() , there exist $z_1,\,z_2\in \operatorname {Cu} (A)$
, there exist $z_1,\,z_2\in \operatorname {Cu} (A)$![]() such that $x'\leq z_1+z_2\leq x$
such that $x'\leq z_1+z_2\leq x$![]() . Examples of dimension zero include the Cuntz semigroup of any real rank zero $\mathrm {C}^*$
. Examples of dimension zero include the Cuntz semigroup of any real rank zero $\mathrm {C}^*$![]() -algebra, as well as other semigroups, such as the Cuntz semigroup of the Jacelon–Razak algebra; see [Reference Thiel and Vilalta50, Section 5].
-algebra, as well as other semigroups, such as the Cuntz semigroup of the Jacelon–Razak algebra; see [Reference Thiel and Vilalta50, Section 5].
We say that a Cuntz semigroup is weakly cancellative if $x\ll y$![]() whenever $x+z\ll y+z$
whenever $x+z\ll y+z$![]() for some element $z$
for some element $z$![]() . Stable rank one $\mathrm {C}^*$
. Stable rank one $\mathrm {C}^*$![]() -algebras have a weakly cancellative Cuntz semigroup by [Reference Rørdam and Winter44, Theorem 4.3].
-algebras have a weakly cancellative Cuntz semigroup by [Reference Rørdam and Winter44, Theorem 4.3].
Corollary 4.13 Let $A$![]() be a simple, non-elementary $\mathrm {C}^*$
be a simple, non-elementary $\mathrm {C}^*$![]() -algebra of Cuntz covering dimension zero. Assume that $\operatorname {Cu} (A)$
-algebra of Cuntz covering dimension zero. Assume that $\operatorname {Cu} (A)$![]() is weakly cancellative. Then there exists $n\in {\mathbb {N}}$
is weakly cancellative. Then there exists $n\in {\mathbb {N}}$![]() such that $\operatorname {div}_{2} ([a])\leq n$
such that $\operatorname {div}_{2} ([a])\leq n$![]() for every $[a]\in \operatorname {Cu} (A)$
for every $[a]\in \operatorname {Cu} (A)$![]() .
.
Proof. Assume first that $A$![]() is separable. [Reference Thiel and Vilalta50, Theorem 7.10] shows that the submonoid $\operatorname {Cu} (A)_{\rm {soft}}$
is separable. [Reference Thiel and Vilalta50, Theorem 7.10] shows that the submonoid $\operatorname {Cu} (A)_{\rm {soft}}$![]() is a retract of an almost divisible Cu-semigroup $S$
is a retract of an almost divisible Cu-semigroup $S$![]() ; see also the proof of [Reference Thiel and Vilalta50, Proposition 7.13].
; see also the proof of [Reference Thiel and Vilalta50, Proposition 7.13].
As explained in example 3.11, almost divisibility implies $\operatorname {div}_2(s)\leq 3$![]() for every element $s\in S$
for every element $s\in S$![]() . Thus, the result in this case follows from corollary 4.12 above.
. Thus, the result in this case follows from corollary 4.12 above.
If $A$![]() is not separable, one can use the same techniques as in the proof of proposition 4.3 to get the desired result.
is not separable, one can use the same techniques as in the proof of proposition 4.3 to get the desired result.
5. Nowhere scattered corona and multiplier algebras
In this section, we study when a multiplier algebra of a $\sigma$![]() -unital, nowhere scattered $\mathrm {C}^*$
-unital, nowhere scattered $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() is nowhere scattered. Our main result is that this happens whenever $\sup _{a\in A_+}\operatorname {div}_{2m}(m[a])<\infty$
is nowhere scattered. Our main result is that this happens whenever $\sup _{a\in A_+}\operatorname {div}_{2m}(m[a])<\infty$![]() for some $m\in {\mathbb {N}}$
for some $m\in {\mathbb {N}}$![]() ; see theorem 5.11. Note that the supremum is not taken over all the elements of the Cuntz semigroup (i.e. over $A\otimes \mathcal {K}$
; see theorem 5.11. Note that the supremum is not taken over all the elements of the Cuntz semigroup (i.e. over $A\otimes \mathcal {K}$![]() ), but only over those with a representative in $A_+$
), but only over those with a representative in $A_+$![]() . This set is called the scale of the Cuntz semigroup in [Reference Antoine, Perera and Thiel4, 4.2].
. This set is called the scale of the Cuntz semigroup in [Reference Antoine, Perera and Thiel4, 4.2].
As an application, we prove in theorem 5.12 that nowhere scattered $\mathrm {C}^*$![]() -algebras of finite nuclear dimension, or real rank zero, or stable rank one and $k$
-algebras of finite nuclear dimension, or real rank zero, or stable rank one and $k$![]() -comparison all have a nowhere scattered multiplier algebra. We also show in theorem 5.18 that, for stable $\mathrm {C}^*$
-comparison all have a nowhere scattered multiplier algebra. We also show in theorem 5.18 that, for stable $\mathrm {C}^*$![]() -algebras, the multiplier algebra being nowhere scattered implies that every element in the algebra has finite weak divisibility.
-algebras, the multiplier algebra being nowhere scattered implies that every element in the algebra has finite weak divisibility.
Let us begin the section with some examples:
Example 5.1 Let $A$![]() be a weakly purely infinite $\mathrm {C}^*$
be a weakly purely infinite $\mathrm {C}^*$![]() -algebra. It was shown in [Reference Kirchberg and Rørdam25, Proposition 4.11] that $\mathcal {M}(A)$
-algebra. It was shown in [Reference Kirchberg and Rørdam25, Proposition 4.11] that $\mathcal {M}(A)$![]() is weakly purely infinite, and thus nowhere scattered by [Reference Thiel and Vilalta49, Example 3.3].
is weakly purely infinite, and thus nowhere scattered by [Reference Thiel and Vilalta49, Example 3.3].
As a similar example, it follows from [Reference Lin32] that a simple, $\sigma$![]() -unital, non-elementary (i.e. nowhere scattered) $\mathrm {C}^*$
-unital, non-elementary (i.e. nowhere scattered) $\mathrm {C}^*$![]() -algebra with continuous scale has a purely infinite corona algebra. This implies that $\mathcal {M}(A)$
-algebra with continuous scale has a purely infinite corona algebra. This implies that $\mathcal {M}(A)$![]() is nowhere scattered by [Reference Thiel and Vilalta49, Proposition 4.2]; see also [Reference Kaftal, Ng and Zhang23] and [Reference Lin30].
is nowhere scattered by [Reference Thiel and Vilalta49, Proposition 4.2]; see also [Reference Kaftal, Ng and Zhang23] and [Reference Lin30].
The examples below appeared in [Reference Thiel and Vilalta49, Examples 4.14, 4.15]. We recall them here for the convenience of the reader.
Example 5.2 Let $A_k$![]() be the family of separable, simple, AH-algebras from [Reference Robert and Rørdam40] (see example 3.6). As shown in [Reference Robert and Rørdam40, Corollary 8.6], the product $\prod _k A_k$
be the family of separable, simple, AH-algebras from [Reference Robert and Rørdam40] (see example 3.6). As shown in [Reference Robert and Rørdam40, Corollary 8.6], the product $\prod _k A_k$![]() has a one-dimensional, irreducible representation. By [Reference Thiel and Vilalta49, Theorem 3.1], this implies that $\prod _k A_k$
has a one-dimensional, irreducible representation. By [Reference Thiel and Vilalta49, Theorem 3.1], this implies that $\prod _k A_k$![]() is not nowhere scattered. Consequently, $A:=\oplus A_k$
is not nowhere scattered. Consequently, $A:=\oplus A_k$![]() is a nowhere scattered $\mathrm {C}^*$
is a nowhere scattered $\mathrm {C}^*$![]() -algebra with a multiplier algebra $\mathcal {M}(A)\cong \prod _k A_k$
-algebra with a multiplier algebra $\mathcal {M}(A)\cong \prod _k A_k$![]() that is not nowhere scattered.
that is not nowhere scattered.
Example 5.3 In [Reference Sakai45, Theorem 1], Sakai constructs a simple $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() such that its derived algebra $D(A)$
such that its derived algebra $D(A)$![]() satisfies $D(A)/A\cong {\mathbb {C}}$
satisfies $D(A)/A\cong {\mathbb {C}}$![]() . Using that $D(A)\cong \mathcal {M}(A)$
. Using that $D(A)\cong \mathcal {M}(A)$![]() for simple $\mathrm {C}^*$
for simple $\mathrm {C}^*$![]() -algebras (see the remarks after [Reference Pedersen35, Proposition 2.6]), one sees that $\mathcal {M}(A)$
-algebras (see the remarks after [Reference Pedersen35, Proposition 2.6]), one sees that $\mathcal {M}(A)$![]() cannot be nowhere scattered.
cannot be nowhere scattered.
The following lemma will play an important role in the proof of proposition 5.9.
Lemma 5.4 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra. The following are equivalent:
-algebra. The following are equivalent:
(i) $A$
 is nowhere scattered.
is nowhere scattered.(ii) For every $a\in A_+$
 and $n\in {\mathbb {N}}$
and $n\in {\mathbb {N}}$ , the class $[a\otimes 1_n]\in \operatorname {Cu} (A)$
, the class $[a\otimes 1_n]\in \operatorname {Cu} (A)$ is weakly $(2n,\,\omega )$
is weakly $(2n,\,\omega )$ -divisible.
-divisible.(iii) For every $a\in A_+$
 , there exists $n=n(a)\in {\mathbb {N}}$
, there exists $n=n(a)\in {\mathbb {N}}$ such that the class $[a\otimes 1_{n}]\in \operatorname {Cu} (A)$
such that the class $[a\otimes 1_{n}]\in \operatorname {Cu} (A)$ is weakly $(n+1,\,\omega )$
is weakly $(n+1,\,\omega )$ -divisible.
-divisible.
Proof. We know from [Reference Thiel and Vilalta49, Theorem 8.9] that $A$![]() is nowhere scattered if and only if every element in $\operatorname {Cu} (A)$
is nowhere scattered if and only if every element in $\operatorname {Cu} (A)$![]() is weakly $(2,\,\omega )$
is weakly $(2,\,\omega )$![]() -divisible. Using [Reference Thiel and Vilalta49, Theorem 8.9], it follows that every element is $(2n,\,\omega )$
-divisible. Using [Reference Thiel and Vilalta49, Theorem 8.9], it follows that every element is $(2n,\,\omega )$![]() -divisible for every $n\in {\mathbb {N}}$
-divisible for every $n\in {\mathbb {N}}$![]() . This proves that (i) implies (ii), and it is trivial that (ii) implies (iii).
. This proves that (i) implies (ii), and it is trivial that (ii) implies (iii).
To see that (iii) implies (i), assume for the sake of contradiction that $A$![]() is not nowhere scattered. Then, we know from [Reference Thiel and Vilalta49, Theorem 3.1] that there exist ideals $I\subseteq J\subseteq A$
is not nowhere scattered. Then, we know from [Reference Thiel and Vilalta49, Theorem 3.1] that there exist ideals $I\subseteq J\subseteq A$![]() such that $J/I$
such that $J/I$![]() is elementary, that is, $\operatorname {Cu} (I/J)\cong \operatorname {Cu} (\mathbb {C})\cong \overline {{\mathbb {N}}}$
is elementary, that is, $\operatorname {Cu} (I/J)\cong \operatorname {Cu} (\mathbb {C})\cong \overline {{\mathbb {N}}}$![]() ; see [Reference Engbers19, Theorem 4.4.4].
; see [Reference Engbers19, Theorem 4.4.4].
Note that, since we are assuming that $A$![]() satisfies (iii), both $I$
satisfies (iii), both $I$![]() and $I/J$
and $I/J$![]() satisfy (iii) as well. Let $\phi$
satisfy (iii) as well. Let $\phi$![]() be an isomorphism from $\operatorname {Cu} (I/J)$
be an isomorphism from $\operatorname {Cu} (I/J)$![]() to $\overline {{\mathbb {N}}}$
to $\overline {{\mathbb {N}}}$![]() . Now, it follows from [Reference Thiel and Vilalta51, Lemma 3.3] that for every positive element $b\in (I/J)\otimes \mathcal {K}$
. Now, it follows from [Reference Thiel and Vilalta51, Lemma 3.3] that for every positive element $b\in (I/J)\otimes \mathcal {K}$![]() there exists $a\in (I/J)_+$
there exists $a\in (I/J)_+$![]() such that $[b]\leq \infty [a]$
such that $[b]\leq \infty [a]$![]() in $\operatorname {Cu} (I/J)$
in $\operatorname {Cu} (I/J)$![]() . Thus, let $a\in (I/J)_+$
. Thus, let $a\in (I/J)_+$![]() be such that $\phi ([a])\neq 0$
be such that $\phi ([a])\neq 0$![]() . We get $1\ll 1\leq \phi ([a])$
. We get $1\ll 1\leq \phi ([a])$![]() and, using Rørdam's lemma (see e.g. [Reference Thiel46, Theorem 2.30]), there exists $a'\in (I/J)_+$
and, using Rørdam's lemma (see e.g. [Reference Thiel46, Theorem 2.30]), there exists $a'\in (I/J)_+$![]() such that $1=\phi ([a'])$
such that $1=\phi ([a'])$![]() .
.
Take $n\in {\mathbb {N}}$![]() such that $[a'\otimes 1_n]$
such that $[a'\otimes 1_n]$![]() is weakly $(n+1,\,\omega )$
is weakly $(n+1,\,\omega )$![]() -divisible. Since $\phi$
-divisible. Since $\phi$![]() is an isomorphism, we must have that $\phi ([a'\otimes 1_n])=n$
is an isomorphism, we must have that $\phi ([a'\otimes 1_n])=n$![]() is also weakly $(n+1,\,\omega )$
is also weakly $(n+1,\,\omega )$![]() -divisible. However, the only element $x\in \overline {{\mathbb {N}}}$
-divisible. However, the only element $x\in \overline {{\mathbb {N}}}$![]() such that $(n+1)x\leq n$
such that $(n+1)x\leq n$![]() is zero. This contradicts the weak $(n+1,\,\omega )$
is zero. This contradicts the weak $(n+1,\,\omega )$![]() -divisibility of $[a'\otimes 1_n]$
-divisibility of $[a'\otimes 1_n]$![]() .
.
Thus, $A$![]() has no nonzero elementary ideal-quotients, as desired.
has no nonzero elementary ideal-quotients, as desired.
Remark 5.5 In the proof of ‘(iii)$\implies$![]() (i)’ in lemma 5.4 above, we have used that a $\mathrm {C}^*$
(i)’ in lemma 5.4 above, we have used that a $\mathrm {C}^*$![]() -algebra is nowhere scattered if and only if it has no elementary ideal-quotients. As shown in [Reference Thiel and Vilalta49, Proposition 8.8], a Cu-semigroup $S$
-algebra is nowhere scattered if and only if it has no elementary ideal-quotients. As shown in [Reference Thiel and Vilalta49, Proposition 8.8], a Cu-semigroup $S$![]() satisfying (O5)–(O8) has no elementary ideal-quotients if and only if every element in $S$
satisfying (O5)–(O8) has no elementary ideal-quotients if and only if every element in $S$![]() is weakly $(2,\,\omega )$
is weakly $(2,\,\omega )$![]() -divisible.
-divisible.
In light of this, one might expect ‘(iii)$\implies$![]() (i)’ to hold for every Cu-semigroup $S$
(i)’ to hold for every Cu-semigroup $S$![]() satisfying (O5)–(O8), that is, that every element in $S$
satisfying (O5)–(O8), that is, that every element in $S$![]() is weakly $(2,\,\omega )$
is weakly $(2,\,\omega )$![]() -divisible whenever for every element $x\in S$
-divisible whenever for every element $x\in S$![]() there exists $n_x$
there exists $n_x$![]() such that $n_x x$
such that $n_x x$![]() is weakly $(n_x +1,\,\omega )$
is weakly $(n_x +1,\,\omega )$![]() -divisible.
-divisible.
However, this is not true: For example, $S=\{ 0,\,1,\,\infty \}$![]() is a Cu-semigroup satisfying (O5)–(O8). $S$
is a Cu-semigroup satisfying (O5)–(O8). $S$![]() is not weakly $(2,\,\omega )$
is not weakly $(2,\,\omega )$![]() -divisible, but every element in $S$
-divisible, but every element in $S$![]() has a properly infinite multiple. Thus, it satisfies (iii), but not (i).
has a properly infinite multiple. Thus, it satisfies (iii), but not (i).
The reason for this disparity is due to the fact that, in the context of abstract Cuntz semigroups, $\overline {{\mathbb {N}}}$![]() is not the only elementary Cu-semigroup. In fact, $\{ 0,\,1,\,\infty \}$
is not the only elementary Cu-semigroup. In fact, $\{ 0,\,1,\,\infty \}$![]() is elementary; see [Reference Thiel and Vilalta49, Section 8].
is elementary; see [Reference Thiel and Vilalta49, Section 8].
Lemma 5.6 below is [Reference Kirchberg and Rørdam25, Lemma 4.10], which uses some of the ideas from [Reference Elliott16]. It was stated with the assumption of weak pure infiniteness, but an inspection of their proof shows that this is not actually needed. This was also stated, in a different way and with a different proof, in [Reference Kaftal, Ng and Zhang22, Theorem 4.2].
Note that both of the strictly convergent sums in the right-hand side consist of pairwise orthogonal terms.
Lemma 5.6 Let $A$![]() be a $\sigma$
be a $\sigma$![]() -unital $\mathrm {C}^*$
-unital $\mathrm {C}^*$![]() -algebra, let $T\in \mathcal {M}(A)_+$
-algebra, let $T\in \mathcal {M}(A)_+$![]() and let $\varepsilon >0$
and let $\varepsilon >0$![]() . Then $A$
. Then $A$![]() has an increasing, countable, approximate unit $(e_n)_n$
has an increasing, countable, approximate unit $(e_n)_n$![]() of positive contractions with $e_{n+1}e_n=e_n$
of positive contractions with $e_{n+1}e_n=e_n$![]() such that
such that

with $e_0=0$![]() and $a\in A$
and $a\in A$![]() satisfying $\Vert a \Vert \leq \varepsilon$
satisfying $\Vert a \Vert \leq \varepsilon$![]() .
.
In the proof of proposition 5.9 we will also need the following:
Lemma 5.7 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra, and let $a,\,b\in A_+$
-algebra, and let $a,\,b\in A_+$![]() be elements such that $[a],\,[b]\in \operatorname {Cu} (A)$
be elements such that $[a],\,[b]\in \operatorname {Cu} (A)$![]() have multiples of finite weak divisibility. Then, $[a+b]$
have multiples of finite weak divisibility. Then, $[a+b]$![]() has a multiple of finite weak divisibility.
has a multiple of finite weak divisibility.
In particular, there exists $n\in {\mathbb {N}}$![]() such that $(a+b)\otimes 1_{n}$
such that $(a+b)\otimes 1_{n}$![]() has a $(n+1 ,\,\omega )$
has a $(n+1 ,\,\omega )$![]() -divisible class.
-divisible class.
Proof. Let $n_a,\,n_b\in {\mathbb {N}}$![]() be such that $\operatorname {div}_{2n_a}(n_a[a]),\,\operatorname {div}_{2n_b}(n_b[b])<\infty$
be such that $\operatorname {div}_{2n_a}(n_a[a]),\,\operatorname {div}_{2n_b}(n_b[b])<\infty$![]() .
.
Using that $n_a n_b[a+b]=[a\otimes 1_{n_a n_b} + b\otimes 1_{n_a n_b}]$![]() , we can apply lemma 3.3 (iii) and get
, we can apply lemma 3.3 (iii) and get
Thus, applying lemma 3.4 to both summands, we obtain
as desired.
Lemma 5.8 Let $A$![]() be a $\sigma$
be a $\sigma$![]() -unital $\mathrm {C}^*$
-unital $\mathrm {C}^*$![]() -algebra, and let $(a_i)_{i=1}^\infty$
-algebra, and let $(a_i)_{i=1}^\infty$![]() be a bounded sequence in $A$
be a bounded sequence in $A$![]() of pairwise orthogonal elements such that $R=\sum _i a_i$
of pairwise orthogonal elements such that $R=\sum _i a_i$![]() is strictly convergent and $a_i\perp e_{i-1}$
is strictly convergent and $a_i\perp e_{i-1}$![]() for every $i\geq 1$
for every $i\geq 1$![]() , where $(e_i)_i$
, where $(e_i)_i$![]() is an approximate unit as in lemma 5.6.
is an approximate unit as in lemma 5.6.
Let $m\in {\mathbb {N}}$![]() . Then for every $\varepsilon _0 >0$
. Then for every $\varepsilon _0 >0$![]() , one has
, one has
in $\operatorname {Cu} (\mathcal {M}(A))$![]() .
.
Proof. Let $\varepsilon _0>0$![]() . Assume that $n:=\sup _i\sup _{\varepsilon \leq \varepsilon _0} \operatorname {div}_{2m}(m[(a_i-\varepsilon )_+])$
. Assume that $n:=\sup _i\sup _{\varepsilon \leq \varepsilon _0} \operatorname {div}_{2m}(m[(a_i-\varepsilon )_+])$![]() is finite, since otherwise there is nothing to prove. Fix $\varepsilon \leq \varepsilon _0$
is finite, since otherwise there is nothing to prove. Fix $\varepsilon \leq \varepsilon _0$![]() positive. By assumption, $(a_i-\tfrac {\varepsilon }{4})_+\otimes 1_m$
positive. By assumption, $(a_i-\tfrac {\varepsilon }{4})_+\otimes 1_m$![]() is weakly $(2m,\,n)$
is weakly $(2m,\,n)$![]() -divisible for each $i$
-divisible for each $i$![]() . Thus, we can find elements $b_{i,j}\in A\otimes \mathcal {K}$
. Thus, we can find elements $b_{i,j}\in A\otimes \mathcal {K}$![]() for $j=1,\,\ldots,\, n$
for $j=1,\,\ldots,\, n$![]() such that
such that
for each $i$![]() and $j$
and $j$![]() .
.
It follows from [Reference Robert and Rørdam40, Lemma 2.3(i)] that there exist elements $c_{i,j}\in M_m(A)_+$![]() with $c_{i,j}\precsim b_{i,j}$
with $c_{i,j}\precsim b_{i,j}$![]() such that
such that

Set $d_{i,j}:= ((a_i - 2\varepsilon /3 )_+\otimes 1_m) c_{i,j} ((a_i - 2\varepsilon /3)_+\otimes 1_m)\in M_m (A)$![]() . Note that every entry in $d_{i,j}$
. Note that every entry in $d_{i,j}$![]() is in $\overline {a_i Aa_i}$
is in $\overline {a_i Aa_i}$![]() , and is thus orthogonal with $e_{i-1}$
, and is thus orthogonal with $e_{i-1}$![]() . To see that the sums $R_j := \sum _{i} d_{i,j}$
. To see that the sums $R_j := \sum _{i} d_{i,j}$![]() are strictly convergent, we proceed as in [Reference Kaftal, Ng and Zhang22, Proposition 4.4]. Using that $c_{i,j}\leq a_i\otimes 1_m$
are strictly convergent, we proceed as in [Reference Kaftal, Ng and Zhang22, Proposition 4.4]. Using that $c_{i,j}\leq a_i\otimes 1_m$![]() at the third step, we have
at the third step, we have

where note that the supremum over $i$![]() is finite because the sequence $(a_i)_i$
is finite because the sequence $(a_i)_i$![]() is bounded.
is bounded.
Now, given any $t\in M_m (A)$![]() and any pair $n< k$
and any pair $n< k$![]() , and using that the $d_{i,j}$
, and using that the $d_{i,j}$![]() 's are pairwise orthogonal on $i$
's are pairwise orthogonal on $i$![]() (and that so are the $a_i$
(and that so are the $a_i$![]() 's), one has
's), one has

and, similarly,

Since $\sum _i a_i$![]() is strictly convergent, so is $\sum _{i} (a_i - 2\varepsilon /3 )_+\otimes 1_m$
is strictly convergent, so is $\sum _{i} (a_i - 2\varepsilon /3 )_+\otimes 1_m$![]() . Thus, it follows that $R_j=\sum _i d_{i,j}$
. Thus, it follows that $R_j=\sum _i d_{i,j}$![]() is a strictly convergent sum. Further, note that we have
is a strictly convergent sum. Further, note that we have

and, therefore, $m[(R-\varepsilon )_+]\ll \sum _{j=1}^n [R_j]$![]() .
.
Let $\delta >0$![]() be such that $m[(R-\varepsilon )_+]\leq \sum _{j=1}^n [(R_j -\delta )_+]$
be such that $m[(R-\varepsilon )_+]\leq \sum _{j=1}^n [(R_j -\delta )_+]$![]() . Applying [Reference Kaftal, Ng and Zhang22, Lemma 2.2] at
. Applying [Reference Kaftal, Ng and Zhang22, Lemma 2.2] at
we find elements $r_{i,j}$![]() such that
such that
Set $x_{i,j}:= (a_i\otimes 1_m)^{1/2}r_{i,j}^* (d_{i,j}\otimes 1_{2m}-\delta )_+$![]() . We get
. We get
with both $((a_i\otimes 1_m)^{1/2}r_{i,j}^*)_i$![]() and $( r_{i,j}^* (d_{i,j}\otimes 1_{2m}-\delta )_+)_i$
and $( r_{i,j}^* (d_{i,j}\otimes 1_{2m}-\delta )_+)_i$![]() being bounded sequences for each fixed $j$
being bounded sequences for each fixed $j$![]() .
.
Let $j$![]() be fixed. To see that $\sum _i x_{i,j}$
be fixed. To see that $\sum _i x_{i,j}$![]() is strictly convergent, we argue as before. First, note that one has
is strictly convergent, we argue as before. First, note that one has

where each suprema is bounded because $(d_{i,j})_i$![]() is a bounded sequence.
is a bounded sequence.
For any given pair $n< k$![]() and any $t$
and any $t$![]() , one has
, one has

Let $x_{i,j}(s,\,r)$![]() denote the $(s,\,r)$
denote the $(s,\,r)$![]() -th entry of $x_{i,j}$
-th entry of $x_{i,j}$![]() . Then, the sums $x_{j}(s,\,r):=\sum _i x_{i,j}(s,\,r)$
. Then, the sums $x_{j}(s,\,r):=\sum _i x_{i,j}(s,\,r)$![]() are all strictly convergent. Set $x_{j}:=(x_{j}(s,\,r))_{s,r}\in M_{m,2m^2}(\mathcal {M}(A))$
are all strictly convergent. Set $x_{j}:=(x_{j}(s,\,r))_{s,r}\in M_{m,2m^2}(\mathcal {M}(A))$![]() . One gets
. One gets
and
It follows that, in $\operatorname {Cu} (\mathcal {M}(A))$![]() , we have $2m[(R_j-\delta )_+]\leq m[R]$
, we have $2m[(R_j-\delta )_+]\leq m[R]$![]() for each $j\in {\mathbb {N}}$
for each $j\in {\mathbb {N}}$![]() . Since $[R]=\sup _{0\leq \varepsilon \leq \varepsilon _0}[(R-\varepsilon )_+]$
. Since $[R]=\sup _{0\leq \varepsilon \leq \varepsilon _0}[(R-\varepsilon )_+]$![]() , we have that $m[R]$
, we have that $m[R]$![]() is weakly $(2m,\,n)$
is weakly $(2m,\,n)$![]() -divisible, as desired.
-divisible, as desired.
Let us say that a sequence $(a_i)_i$![]() of positive elements in a $\mathrm {C}^*$
of positive elements in a $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() is orthogonal if the elements in the sequence are pairwise orthogonal, that is, if $a_i a_j=0$
is orthogonal if the elements in the sequence are pairwise orthogonal, that is, if $a_i a_j=0$![]() whenever $i\neq j$
whenever $i\neq j$![]() .
.
Proposition 5.9 Let $A$![]() be a $\sigma$
be a $\sigma$![]() -unital $\mathrm {C}^*$
-unital $\mathrm {C}^*$![]() -algebra. Assume that for every orthogonal sequence $(a_i)_i$
-algebra. Assume that for every orthogonal sequence $(a_i)_i$![]() of positive elements in $A$
of positive elements in $A$![]() there exist $m,\,n\in {\mathbb {N}}$
there exist $m,\,n\in {\mathbb {N}}$![]() such that $\operatorname {div}_{2m} (m[a_i])\leq n$
such that $\operatorname {div}_{2m} (m[a_i])\leq n$![]() for each $i$
for each $i$![]() . Then $\operatorname {div}_{2m} (m[T])<\infty$
. Then $\operatorname {div}_{2m} (m[T])<\infty$![]() for every $T\in \mathcal {M}(A)/A$
for every $T\in \mathcal {M}(A)/A$![]() .
.
In particular, $\mathcal {M}(A)/A$![]() is nowhere scattered.
is nowhere scattered.
Proof. Let $\pi \colon \mathcal {M}(A)\to \mathcal {M}(A)/A$![]() denote the quotient map. Using lemmas 5.6 and 5.8, we deduce that each positive element in the corona algebra can be written as $\pi (R_1)+\pi (R_2)$
denote the quotient map. Using lemmas 5.6 and 5.8, we deduce that each positive element in the corona algebra can be written as $\pi (R_1)+\pi (R_2)$![]() with $[R_1],\, [R_2]$
with $[R_1],\, [R_2]$![]() having multiples of finite weak divisibility.
having multiples of finite weak divisibility.
By lemma 5.7, every element of the form $[\pi (T)]$![]() in $\operatorname {Cu} (\mathcal {M}(A)/A)$
in $\operatorname {Cu} (\mathcal {M}(A)/A)$![]() with $T\in (\mathcal {M}(A)/A)_+$
with $T\in (\mathcal {M}(A)/A)_+$![]() has a multiple of finite weak divisibility. Lemma 5.4 shows that the corona algebra is nowhere scattered, as desired.
has a multiple of finite weak divisibility. Lemma 5.4 shows that the corona algebra is nowhere scattered, as desired.
Remark 5.10 Let $A$![]() be the simple, nowhere scattered $\mathrm {C}^*$
be the simple, nowhere scattered $\mathrm {C}^*$![]() -algebra from example 5.3. It follows from proposition 5.9 above that there must exist an element $a\in (\oplus _{i=1}^\infty A)_+$
-algebra from example 5.3. It follows from proposition 5.9 above that there must exist an element $a\in (\oplus _{i=1}^\infty A)_+$![]() whose Cuntz class does not have a multiple of finite weak divisibility.
whose Cuntz class does not have a multiple of finite weak divisibility.
Using proposition 5.9, we can now prove the main result of the paper.
Theorem 5.11 Let $A$![]() be a $\sigma$
be a $\sigma$![]() -unital $\mathrm {C}^*$
-unital $\mathrm {C}^*$![]() -algebra. Assume that for every orthogonal sequence $(a_i)_i$
-algebra. Assume that for every orthogonal sequence $(a_i)_i$![]() in $A_+$
in $A_+$![]() there exist $m,\,n\in {\mathbb {N}}$
there exist $m,\,n\in {\mathbb {N}}$![]() such that $\operatorname {div}_{2m} (m[a_i])\leq n$
such that $\operatorname {div}_{2m} (m[a_i])\leq n$![]() for each $i$
for each $i$![]() . Then $\mathcal {M}(A)$
. Then $\mathcal {M}(A)$![]() is nowhere scattered.
is nowhere scattered.
Proof. Using that nowhere scatteredness works well with extensions (see [Reference Thiel and Vilalta49, Proposition 4.2]), the result is a direct consequence of proposition 5.9.
It follows from the results in [Reference Perera and Rørdam37] that the multiplier algebra of a simple, separable $\mathrm {C}^*$![]() -algebra of real rank zero does not admit a character. Theorem 5.12 (i) below generalizes this result.
-algebra of real rank zero does not admit a character. Theorem 5.12 (i) below generalizes this result.
Theorem 5.12 Let $A$![]() be a $\sigma$
be a $\sigma$![]() -unital $\mathrm {C}^*$
-unital $\mathrm {C}^*$![]() -algebra. Assume that $A$
-algebra. Assume that $A$![]() has
has
(i) real rank zero, or
(ii) finite nuclear dimension, or
(iii) $k$
 -comparison and a surjective rank map.
-comparison and a surjective rank map.
Then $A$![]() is nowhere scattered if and only if $\mathcal {M}(A)$
is nowhere scattered if and only if $\mathcal {M}(A)$![]() is nowhere scattered.
is nowhere scattered.
Proof. Assume that $\mathcal {M}(A)$![]() is nowhere scattered. [Reference Thiel and Vilalta49, Proposition 4.2] implies that $A$
is nowhere scattered. [Reference Thiel and Vilalta49, Proposition 4.2] implies that $A$![]() is nowhere scattered as well.
is nowhere scattered as well.
Conversely, assume that $A$![]() is nowhere scattered. It follows from example 3.11, proposition 4.1 and proposition 4.3 respectively that (i), (ii) and (iii) imply that every sequence of positive elements (orthogonal or not) in $A_+$
is nowhere scattered. It follows from example 3.11, proposition 4.1 and proposition 4.3 respectively that (i), (ii) and (iii) imply that every sequence of positive elements (orthogonal or not) in $A_+$![]() has uniformly bounded multiple divisibility. Thus, we can use theorem 5.11 to get the desired result.
has uniformly bounded multiple divisibility. Thus, we can use theorem 5.11 to get the desired result.
Question 5.13 Let $A$![]() be a nowhere scattered $\mathrm {C}^*$
be a nowhere scattered $\mathrm {C}^*$![]() -algebra such that $[a]$
-algebra such that $[a]$![]() has a multiple of finite weak divisibility for every $a\in A_+$
has a multiple of finite weak divisibility for every $a\in A_+$![]() . Does it follow that $\mathcal {M}(A)$
. Does it follow that $\mathcal {M}(A)$![]() is nowhere scattered?
is nowhere scattered?
Note that this would imply that the simple $\mathrm {C}^*$![]() -algebra from example 5.3 contains a $(2,\,\omega )$
-algebra from example 5.3 contains a $(2,\,\omega )$![]() -divisible element of infinite weak divisibility.
-divisible element of infinite weak divisibility.
Remark 5.14 The assumption from theorem 5.11 above is not equivalent to nowhere scatteredness, not even in the simple or $\sigma$![]() -unital case:
-unital case:
(1) The example from example 5.2 is $\sigma$
 -unital. Thus, there exist $\sigma$
-unital. Thus, there exist $\sigma$ -unital, nowhere scattered $\mathrm {C}^*$
-unital, nowhere scattered $\mathrm {C}^*$ -algebras that do not satisfy the condition from theorem 5.11.
-algebras that do not satisfy the condition from theorem 5.11.(2) By lemma 3.12, the set of classes with finite weak divisibility is sup-dense in the Cuntz semigroup of a simple, non-elementary $\mathrm {C}^*$
 -algebra $A$
-algebra $A$ . However, and as made explicit in example 5.3, this is not enough for the multiplier algebra $\mathcal {M}(A)$
. However, and as made explicit in example 5.3, this is not enough for the multiplier algebra $\mathcal {M}(A)$ to be nowhere scattered.
to be nowhere scattered.
Further, note that if the converse of theorem 5.11 holds for some family of $\mathrm {C}^*$![]() -algebras, one must have that any unital, nowhere scattered $\mathrm {C}^*$
-algebras, one must have that any unital, nowhere scattered $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() in the family must satisfy $\sup _{a\in A_+}\operatorname {div}_{2m} (m[a_i])<\infty$
in the family must satisfy $\sup _{a\in A_+}\operatorname {div}_{2m} (m[a_i])<\infty$![]() for some $m$
for some $m$![]() .
.
As another application of lemma 5.8, we can study when multiplier algebras have a character:
Proposition 5.15 Let $A$![]() be a $\sigma$
be a $\sigma$![]() -unital $\mathrm {C}^*$
-unital $\mathrm {C}^*$![]() -algebra, and let $(e_i)_i$
-algebra, and let $(e_i)_i$![]() be an approximate unit as in lemma 5.6. Assume that
be an approximate unit as in lemma 5.6. Assume that
for some $\varepsilon _0 >0$![]() .
.
Then, $\mathcal {M}(A)$![]() does not admit a character.
does not admit a character.
Proof. Using lemma 5.8, we see that the unit $1=\sum _i (e_i - e_{i-1})$![]() in $\mathcal {M}(A)$
in $\mathcal {M}(A)$![]() satisfies $\operatorname {div}_{2m} (m[1])<\infty$
satisfies $\operatorname {div}_{2m} (m[1])<\infty$![]() .
.
The result now follows from [Reference Robert and Rørdam40, Corollary 5.6].
In particular, proposition 5.15 recovers [Reference Robert and Rørdam40, Corollary 8.5]:
Corollary 5.16 The product of unital $\mathrm {C}^*$![]() -algebras $A_i$
-algebras $A_i$![]() does not admit a character whenever the supremum of $\operatorname {div}_2 ([1_i])$
does not admit a character whenever the supremum of $\operatorname {div}_2 ([1_i])$![]() is finite.
is finite.
5.1 Stable $\mathrm {C}^*$ -algebras
-algebras
The multiplier algebra of a $\sigma$![]() -unital, stable $\mathrm {C}^*$
-unital, stable $\mathrm {C}^*$![]() -algebra $A$
-algebra $A$![]() has been studied extensively. For example, [Reference Rørdam42] studies when the corona algebra of $A$
has been studied extensively. For example, [Reference Rørdam42] studies when the corona algebra of $A$![]() is simple, while in [Reference Ng and Winter34] it is shown, using its multiplier algebra, that a nowhere scattered $\mathrm {C}^*$
is simple, while in [Reference Ng and Winter34] it is shown, using its multiplier algebra, that a nowhere scattered $\mathrm {C}^*$![]() -algebra of finite nuclear dimension has the corona factorization property.
-algebra of finite nuclear dimension has the corona factorization property.
In what follows, we show that $[a]$![]() must have a multiple of finite weak divisibility for every $a\in A_+$
must have a multiple of finite weak divisibility for every $a\in A_+$![]() if $\mathcal {M}(A)$
if $\mathcal {M}(A)$![]() is to be nowhere scattered; see theorem 5.18. Thus, if question 5.13 has an affirmative answer, this would imply that the multiplier algebra of a $\sigma$
is to be nowhere scattered; see theorem 5.18. Thus, if question 5.13 has an affirmative answer, this would imply that the multiplier algebra of a $\sigma$![]() -unital, stable $\mathrm {C}^*$
-unital, stable $\mathrm {C}^*$![]() -algebra is nowhere scattered if and only if every element in the algebra has a multiple of finite weak divisibility.
-algebra is nowhere scattered if and only if every element in the algebra has a multiple of finite weak divisibility.
Lemma 5.17 below was stated for $(m,\,\omega )$![]() -divisibility in [Reference Thiel and Vilalta51]. We now provide the analogous statement for weak $(m,\,\omega )$
-divisibility in [Reference Thiel and Vilalta51]. We now provide the analogous statement for weak $(m,\,\omega )$![]() -divisibility, which only needs to assume the element (and not the whole Cuntz semigroup) to be divisible.
-divisibility, which only needs to assume the element (and not the whole Cuntz semigroup) to be divisible.
Lemma 5.17 Let $A$![]() be a $\mathrm {C}^*$
be a $\mathrm {C}^*$![]() -algebra, and let $a\in (A\otimes \mathcal {K})_+$
-algebra, and let $a\in (A\otimes \mathcal {K})_+$![]() . Then, if $[a]$
. Then, if $[a]$![]() is weakly $(m,\,\omega )$
is weakly $(m,\,\omega )$![]() -divisible, there exists a sequence $(y_n)_n\subseteq \operatorname {Cu} (A)$
-divisible, there exists a sequence $(y_n)_n\subseteq \operatorname {Cu} (A)$![]() such that $my_j\leq [a]\leq \sum _{j=1}^\infty y_j$
such that $my_j\leq [a]\leq \sum _{j=1}^\infty y_j$![]() for every $j\in {\mathbb {N}}$
for every $j\in {\mathbb {N}}$![]() .
.
Proof. Let $\varepsilon _n$![]() be a strictly decreasing sequence converging to $0$
be a strictly decreasing sequence converging to $0$![]() , and let $x_n := [(a-\varepsilon _n )_+]$
, and let $x_n := [(a-\varepsilon _n )_+]$![]() . For each $n$
. For each $n$![]() , apply $(m,\,\omega )$
, apply $(m,\,\omega )$![]() -divisibility to $x_n\ll [a]$
-divisibility to $x_n\ll [a]$![]() to find elements $y_{n,j}$
to find elements $y_{n,j}$![]() such that
such that
for every $j$![]() . In particular, note that one gets
. In particular, note that one gets

By taking supremum on $n$![]() , one sees that the elements $(y_{n,j})_{n,j}$
, one sees that the elements $(y_{n,j})_{n,j}$![]() satisfy the desired conditions.
satisfy the desired conditions.
Note that, in general, one cannot adapt the previous proof to show that there exist $y_1,\,\ldots,\,y_m$![]() with $2y_j\leq [a]\leq y_1+\ldots +y_m$
with $2y_j\leq [a]\leq y_1+\ldots +y_m$![]() whenever $[a]$
whenever $[a]$![]() is $(2,\,m)$
is $(2,\,m)$![]() -divisible.
-divisible.
However, this is the case for $\sigma$![]() -unital $\mathrm {C}^*$
-unital $\mathrm {C}^*$![]() -algebras whose multiplier algebra is nowhere scattered:
-algebras whose multiplier algebra is nowhere scattered:
Theorem 5.18 Let $A$![]() be a $\sigma$
be a $\sigma$![]() -unital, stable $\mathrm {C}^*$
-unital, stable $\mathrm {C}^*$![]() -algebra. Assume that $\mathcal {M}(A)$
-algebra. Assume that $\mathcal {M}(A)$![]() is nowhere scattered. Then, for every $a\in A_+$
is nowhere scattered. Then, for every $a\in A_+$![]() and $m\in {\mathbb {N}}$
and $m\in {\mathbb {N}}$![]() there exist finitely many elements $y_1,\,\ldots,\,y_n\in \operatorname {Cu} (A)$
there exist finitely many elements $y_1,\,\ldots,\,y_n\in \operatorname {Cu} (A)$![]() such that
such that
for every $j\leq n$![]() .
.
In particular, $[a]$![]() has a multiple of finite weak divisibility for every $a\in A_+$
has a multiple of finite weak divisibility for every $a\in A_+$![]() .
.
Proof. Let $a\in A_+$![]() and $m\in {\mathbb {N}}$
and $m\in {\mathbb {N}}$![]() . By [Reference Antoine, Perera, Robert and Thiel2, Proposition 2.8] and its proof there exists a projection $p_a\in \mathcal {M}(A)$
. By [Reference Antoine, Perera, Robert and Thiel2, Proposition 2.8] and its proof there exists a projection $p_a\in \mathcal {M}(A)$![]() such that, for every $x\in \operatorname {Cu} (A)$
such that, for every $x\in \operatorname {Cu} (A)$![]() , one has $x\leq [a]$
, one has $x\leq [a]$![]() if and only if $x\leq [p_a]$
if and only if $x\leq [p_a]$![]() in $\operatorname {Cu} (\mathcal {M}(A))$
in $\operatorname {Cu} (\mathcal {M}(A))$![]() .
.
Assume that $\mathcal {M}(A)$![]() is nowhere scattered. Thus, $\operatorname {Cu} (\mathcal {M}(A))$
is nowhere scattered. Thus, $\operatorname {Cu} (\mathcal {M}(A))$![]() is weakly $(m,\,\omega )$
is weakly $(m,\,\omega )$![]() -divisible by [Reference Thiel and Vilalta49, Theorem 8.9]. It follows from remark 3.2 that $\operatorname {div}_m ([p])<\infty$
-divisible by [Reference Thiel and Vilalta49, Theorem 8.9]. It follows from remark 3.2 that $\operatorname {div}_m ([p])<\infty$![]() for every projection $p\in \mathcal {M}(A)$
for every projection $p\in \mathcal {M}(A)$![]() .
.
Then, since we have $[a]\leq [p_a]\ll [p_a]$![]() , there exist finitely many elements $z_1,\,\ldots,\,z_n$
, there exist finitely many elements $z_1,\,\ldots,\,z_n$![]() in $\operatorname {Cu} (\mathcal {M}(A))$
in $\operatorname {Cu} (\mathcal {M}(A))$![]() such that
such that
for each $j\leq n$![]() .
.
Since $\mathcal {M}(A)$![]() is a $\mathrm {C}^*$
is a $\mathrm {C}^*$![]() -algebra, we know from [Reference Antoine, Perera, Robert and Thiel1, Remark 2.6] that the infimum $y_j:=z_j\wedge \infty [a]$
-algebra, we know from [Reference Antoine, Perera, Robert and Thiel1, Remark 2.6] that the infimum $y_j:=z_j\wedge \infty [a]$![]() exists for each $j$
exists for each $j$![]() . Any representative of this element is contained in the ideal generated by $a$
. Any representative of this element is contained in the ideal generated by $a$![]() and, therefore, must be a positive element in $A$
and, therefore, must be a positive element in $A$![]() . Thus, we have $[a]\leq y_1+\ldots +y_n$
. Thus, we have $[a]\leq y_1+\ldots +y_n$![]() in $\operatorname {Cu} (\mathcal {M}(A))$
in $\operatorname {Cu} (\mathcal {M}(A))$![]() with $y_j\in \operatorname {Cu} (A)$
with $y_j\in \operatorname {Cu} (A)$![]() for each $j$
for each $j$![]() .
.
Further, we also get $my_j=m(z_j\wedge \infty [a])\leq [p_a]$![]() . Thus, $my_j\leq [a]$
. Thus, $my_j\leq [a]$![]() in $\operatorname {Cu} (\mathcal {M}(A))$
in $\operatorname {Cu} (\mathcal {M}(A))$![]() .
.
Finally, note that, since $A$![]() is an ideal of $\mathcal {M}(A)$
is an ideal of $\mathcal {M}(A)$![]() , a pair of elements in $A$
, a pair of elements in $A$![]() are Cuntz subequivalent in $\mathcal {M}(A)$
are Cuntz subequivalent in $\mathcal {M}(A)$![]() if and only if they are Cuntz subequivalent in $A$
if and only if they are Cuntz subequivalent in $A$![]() ; see, for example, [Reference Thiel46, Proposition 2.18].
; see, for example, [Reference Thiel46, Proposition 2.18].
Consequently, we have
in $\operatorname {Cu} (A)$![]() , as desired.
, as desired.
Remark 5.19 Note that there exist stable, nowhere scattered $\mathrm {C}^*$![]() -algebras with a multiplier algebra that is not nowhere scattered. Indeed, simply take $A$
-algebras with a multiplier algebra that is not nowhere scattered. Indeed, simply take $A$![]() as in example 3.6. Then, $A\otimes \mathcal {K}$
as in example 3.6. Then, $A\otimes \mathcal {K}$![]() is a nowhere scattered $\mathrm {C}^*$
is a nowhere scattered $\mathrm {C}^*$![]() -algebra by [Reference Thiel and Vilalta49, Proposition 4.12] that contains a $(2,\,\omega )$
-algebra by [Reference Thiel and Vilalta49, Proposition 4.12] that contains a $(2,\,\omega )$![]() -divisible element of infinite weak divisibility.
-divisible element of infinite weak divisibility.
It follows from theorem 5.18 that $\mathcal {M}(A\otimes \mathcal {K})$![]() cannot be nowhere scattered.
cannot be nowhere scattered.
In this paper, we have studied conditions under which a multiplier algebra $\mathcal {M}(A)$![]() is nowhere scattered. A problem that seems to be much more involved is to determine when $\mathcal {M}(A)$
is nowhere scattered. A problem that seems to be much more involved is to determine when $\mathcal {M}(A)$![]() has the Global Glimm Property.
has the Global Glimm Property.
Question 5.20 Assume that $A$![]() has the Global Glimm Property. When does $\mathcal {M}(A)$
has the Global Glimm Property. When does $\mathcal {M}(A)$![]() also have the Global Glimm Property?
also have the Global Glimm Property?
Note that this has a positive solution whenever $\sup _{a\in A_+}\operatorname {Div}_{2m}(m[a])<\infty$![]() and $\mathcal {M}(A)/A$
and $\mathcal {M}(A)/A$![]() satisfies a condition that ensures that the Global Glimm Problem can be answered affirmatively. For example, Lin and Ng show in [Reference Lin and Ng33] that $\mathcal {M}(\mathcal {Z}\otimes \mathcal {K})/\mathcal {Z}\otimes \mathcal {K}$
satisfies a condition that ensures that the Global Glimm Problem can be answered affirmatively. For example, Lin and Ng show in [Reference Lin and Ng33] that $\mathcal {M}(\mathcal {Z}\otimes \mathcal {K})/\mathcal {Z}\otimes \mathcal {K}$![]() has real rank zero. Thus, since $\mathcal {Z}\otimes \mathcal {K}$
has real rank zero. Thus, since $\mathcal {Z}\otimes \mathcal {K}$![]() is covered by theorem 5.11, we get that $\mathcal {M}(\mathcal {Z}\otimes \mathcal {K})/\mathcal {Z}\otimes \mathcal {K}$
is covered by theorem 5.11, we get that $\mathcal {M}(\mathcal {Z}\otimes \mathcal {K})/\mathcal {Z}\otimes \mathcal {K}$![]() is nowhere scattered. By [Reference Elliott and Rørdam18] (see also [Reference Thiel and Vilalta51, Proposition 7.4]), $\mathcal {M}(\mathcal {Z}\otimes \mathcal {K})/\mathcal {Z}\otimes \mathcal {K}$
is nowhere scattered. By [Reference Elliott and Rørdam18] (see also [Reference Thiel and Vilalta51, Proposition 7.4]), $\mathcal {M}(\mathcal {Z}\otimes \mathcal {K})/\mathcal {Z}\otimes \mathcal {K}$![]() has the Global Glimm Property. Consequently, $\mathcal {M}(\mathcal {Z}\otimes \mathcal {K})$
has the Global Glimm Property. Consequently, $\mathcal {M}(\mathcal {Z}\otimes \mathcal {K})$![]() also has the Global Glimm Property by [Reference Thiel and Vilalta51, Theorem 3.10].
also has the Global Glimm Property by [Reference Thiel and Vilalta51, Theorem 3.10].
Acknowledgements
The author was partially supported by MINECO (grant No. PID2020-113047GB-I00/AEI/10.13039/501100011033 and No. PRE2018-083419), by the Departament de Recerca i Universitats de la Generalitat de Catalunya (grant No. 2021-SGR-01015) and by the Fields Institute for Research in Mathematical Sciences. The author thanks Hannes Thiel for his comments on a first draft of this paper. He also thanks the referee for their valuable suggestions.